Diccionario
Ecuaciones
![]()
![]()

Son muchas las situaciones en las que no podemos hacer una medida porque es imposible realizarla, entonces ¿cómo puedo calcular la longitud de algo que no se puede medir? No puedo coger un metro y medir la altura de la pirámide de Keops o del Everest porque eso es imposible.
Cuando nos ocurren estas cosas, como calcular distancias inabordables o la imposibilidad de utilizar métodos de medida directos (altura de una montaña, rumbo de un barco para llegar a puerto…) tenemos que acudir a nuestros PODERES MATEMÁTICOS. Una de las cosas que vamos a tener que hacer es RESOLVER triángulos, es decir, obtener a partir de unos datos (ángulos o lados de un triángulo) los restantes ángulos y lados. Por ejemplo, si tuviésemos 2 ángulos y un lado, nos faltaría 2 lados y un ángulo por conocer.
Antes de ver cómo se resuelven los triángulos, tenemos que ver nuestras dos ARMAS nuevas y saber cómo funcionan. Se llaman el teorema del seno y el teorema del coseno. Una cuestión muy importante es que estos dos teoremas se aplican a CUALQUIER TIPO de triángulo, no solo a los triángulos rectángulos.
Hay situaciones en las que no puedes medir con un metro
porque es imposible medir.
¿Cómo puedes calcular la longitud de algo que no se puede medir?
Por ejemplo, no puedes medir con un metro
la altura de la montaña más alta.
Es imposible.
Cuando no puedes medir distancias o alturas
porque son imposibles tienes que recurrir
a los poderes matemáticos.
Vas a resolver triángulos.
Con el valor del ángulo o del lado de un triángulo
vas a poder calcular los demás ángulos y lados.
Por ejemplo, si tienes el valor de dos ángulos y un lado,
te faltarían 2 lados y un ángulo por resolver.
Las dos armas matemáticos nuevas son:
El teorema del seno y el teorema del coseno
los puedes aplicar a cualquier tipo de triángulo.
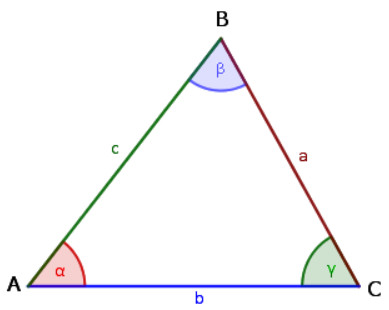
El teorema del seno establece que los lados de cualquier triángulo son proporcionales a los senos de los ángulos opuestos y no solo eso, sino que además la razón de proporcionalidad es el diámetro de la circunferencia circunscrita D:
\frac {a}{sen\ \alpha}\ =\ \frac{b}{sen\ \beta}\ =\ \frac{c}{sen\ \gamma}\ =\ \small{D}
Fíjate que lo que quieren decir esos tres signos igual, es que podemos coger cualquier miembro e igualarlos según nos convenga. Por ejemplo:
\frac {a}{sen\ \alpha}\ =\ \frac{c}{sen\ \gamma}
Observaciones:
Si el triángulo es rectángulo, este teorema se convierte en la definición del seno.
Este teorema nos interesará aplicarlo cuando nos den dos ángulos y un lado o dos lados y un ángulo opuesto a alguno de ellos, pero no nos interesará cuando nos den tres lados o dos lados y el ángulo que no es opuesto a ninguno de ellos, es decir el ángulo comprendido.

El teorema del seno es la relación entre
los lados y los ángulos de cualquier triángulo.
El teorema del seno establece que la relación de la longitud de un lado del triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y es igual para todos los ángulos del triángulo.
La razón de proporcionalidad
es el diámetro de la circunferencia circunscrita D.
\frac {a}{sen\ \alpha}\ =\ \frac{b}{sen\ \beta}\ =\ \frac{c}{sen\ \gamma}\ =\ \small{D}
En este triángulo:
Puedes elegir cualquier fracción e igualarla (ponerle un igual)
con otra de las fracciones.
\frac {a}{sen\ \alpha}\ =\ \frac{c}{sen\ \gamma}
Observaciones:

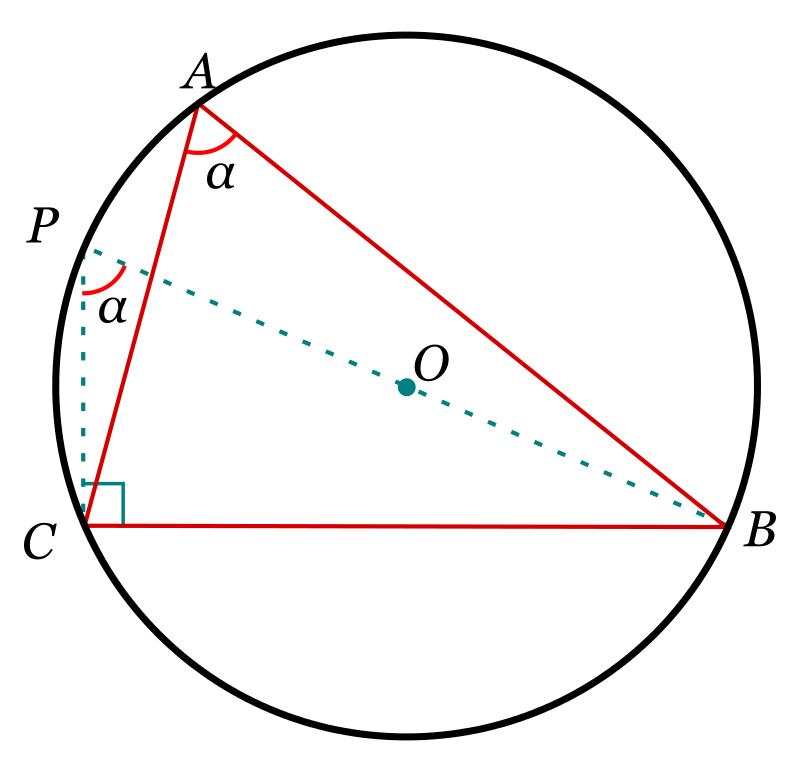
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PCB es recto, puesto que BP es un diámetro, y además los ángulos A y P son congruentes, porque ambos son ángulos inscritos que abren el segmento BC (véase definición de arco capaz). Por definición de la función trigonométrica seno, se tiene:
sen \,A= sen \,P=\frac {BC}{BP}=\frac {a}{2R}
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
\frac {a}{sen \,A}=2R
Repitiendo el procedimiento con un diámetro que pase por A y otro que pase por C, se llega a que las tres fracciones tienen el mismo valor 2R y por tanto son iguales.
Quod erat demonstrandum, QED (CQD)

El teorema del coseno se puede enunciar de la siguiente manera:
El cuadrado del lado opuesto a un ángulo de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de uno de estos por la proyección del otro sobre él.
a^2\ =\ b^2\ +\ c^2\ -\ 2bc\cdot cos\left( \alpha \right) \\ b^2\ =\ a^2\ +\ c^2\ -\ 2ac\cdot cos\left( \beta \right) \\ c^2\ =\ a^2\ +\ b^2\ -\ 2ab\cdot cos\left( \gamma \right)

En un triángulo rectángulo,
el cuadrado de cada lado es igual
a la suma de los cuadrados de los otros lados menos el doble producto de los dos lados por el coseno del ángulo que forman.
Las fórmulas para aplicar el teorema del coseno son:
a^2\ =\ b^2\ +\ c^2\ -\ 2bc\cdot cos\left( \alpha \right) \\ b^2\ =\ a^2\ +\ c^2\ -\ 2ac\cdot cos\left( \beta \right) \\ c^2\ =\ a^2\ +\ b^2\ -\ 2ab\cdot cos\left( \gamma \right)
En este triángulo:
Son datos que se sustituyen en las fórmulas
por los valores que tengas.
En estas fórmulas el primer miembro
es el cuadrado de uno de los lados.
En el segundo miembro aparece una resta
y se introduce el coseno del ángulo opuesto
al primer miembro.
Observa el triángulo que aparece en la imagen.
Por ejemplo:
Observaciones:
Estas son tus dos nuevas y muy poderosas armas.
Fíjate que el segundo miembro es como el desarrollo del cuadrado de una diferencia pero introduciendo el factor coseno del ángulo opuesto al lado del primer miembro
Podemos utilizar cualquiera de las tres ecuaciones según nos convenga y como hemos dicho antes, sirven para cualquier tipo de triángulo.
Observaciones:
Estas son nuestras dos nuevas y muy poderosas armas.
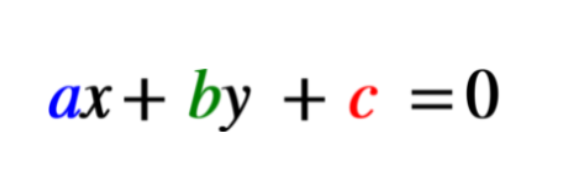
Igualdad matemática entre dos expresiones. Tiene valores conocidos y otros desconocidos representados por letras.
Ejemplo
La ecuación tiene dos incógnitas X e Y.
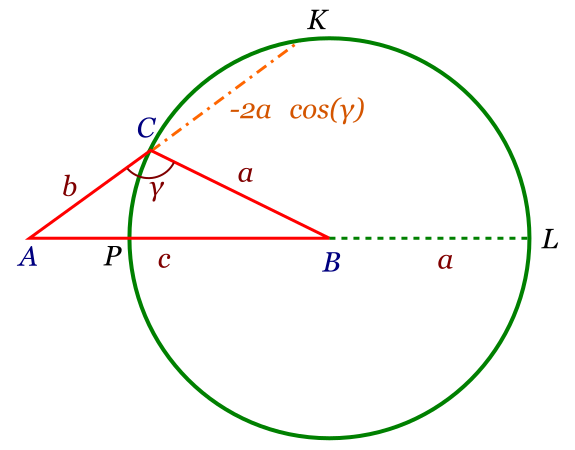
Consideremos un círculo con centro en B y radio BC, como en la figura. Si AC es tangente a la circunferencia, nuevamente se tiene el teorema de Pitágoras ya que \(\gamma\) tendría un valor de 90º. Cuando AC no es tangente, existe otro punto K de corte con el círculo. La potencia del punto A con respecto a dicho círculo es:
AP\cdot AL=AC\cdot AK=AC(AC+CK)
Por otro lado, \(AL = c+a \) y \( AP = c-a\) de modo que:
AP\cdot AL=(c+a)(c-a)=c^{2}-a^{2}
Además, \(CK= -2a cos(\gamma)\) por lo que:
AC(AC+CK)=b(b-2a\,cos(\gamma ))
Igualando las expresiones obtenidas se llega finalmente a:
c^{2}=a^{2}+b^{2}-2a\;b\,\cos(\gamma ) \text{ CQD}
Demostración de por qué $CK= -2a \cdot cos(\gamma)$
Prolongamos el segmento CB hasta cortar nuevamente la circunferencia en un punto D, de modo que CD es un diámetro del círculo, puesto que pasa por el centro del mismo.
Al ser un diámetro, el ángulo inscrito CKD es necesariamente recto puesto que abren el diámetro de la circunferencia, por lo que el triángulo CKD es rectángulo. El ángulo DCK mide $\theta=180°-\gamma$ ya que $ACD+DCK=180º$ y por definición:
\[{\cos(\theta )={\frac {CK}{CD}}={\frac {CK}{2a}}}\]
y por tanto:
\[{CK=2a\cos(\theta )=2a\cos(180^{\circ }-\gamma )=-2a\cos(\gamma )}\]
ya que $cos(180º-x)=-cos(x)$ para cualquier valor de $x$.
Esta teoría ha sido muy interesante.
Seguro que alguna vez te has preguntado: ¿Cómo sabemos cuánto mide una montaña? Aquí has tenido la respuesta. Utilizando el teorema del seno y el teorema del coseno.
Todo lo que aprendes es aplicable a tu vida diaria.
¡Tus poderes se hacen más fuertes!
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0