Diccionario
Análogos

Irracionales
![]()

![]()
Como has podido comprobar, la mayoría de las razones son números irracionales.
De todos los ángulos posibles, hay tres que son especialmente importantes: los ángulos de 30º, 45º y 60º, además de los de 0º y 90º.
Para estos ángulos, se utiliza la expresión exacta, evitando su aproximación decimal. En la siguiente tabla se recoge el valor de las razones trigonométricas para estos ángulos.
| \(sen \) | \(cos \) | \(tg \) | |
| 0º | 0 | 1 | 0 |
| 30º | \( \frac{1}{2} \) | \( \frac{\sqrt{3}}{2} \) | \(\frac{\sqrt{3}}{3} \) |
| 45º | \(\frac {\sqrt{2}}{2} \) | \(\frac {\sqrt{2}}{2} \) | 1 |
| 60º | \(\frac {\sqrt{3}}{2} \) | \(\frac {1}{2} \) | \(\sqrt{3}\) |
| 90º | 1 | 0 | No existe |

Definición
Número con infinitos decimales. No puede expresarse en forma de fracción.
Ejemplo
El número \( \pi\) se clasifica dentro de los números irracionales.
Como has comprobado, la mayoría de las razones trigonométricas
son números irracionales.
Un número irracional es un número que no se puede escribir en fracción.
El número irracional tiene un decimal con cifras infinitas.
Es un número no exacto.
Por ejemplo 3,84673498761238560978… este número es un número irracional.
En las razones trigonométricas se utilizan valores exactos
para evitar el uso de números decimales infinitos.
En la siguiente tabla se recogen los ángulos más importantes
y su valor exacto para las razones de seno, coseno y tangente.
| \(sen \) | \(cos \) | \(tg \) | |
| 0º | 0 | 1 | 0 |
| 30º | \( \frac{1}{2} \) | \( \frac{\sqrt{3}}{2} \) | \(\frac{\sqrt{3}}{3} \) |
| 45º | \(\frac {\sqrt{2}}{2} \) | \(\frac {\sqrt{2}}{2} \) | 1 |
| 60º | \(\frac {\sqrt{3}}{2} \) | \(\frac {1}{2} \) | \(\sqrt{3}\) |
| 90º | 1 | 0 | No existe |
Los ángulos más importantes son:
Ángulos de 0º
Ángulos de 30º
Ángulos de 45º
Ángulos de 60º
Ángulos de 90º
Cuando el ángulo es 0º:
El seno tiene un valor de 0.
El coseno tiene un valor de 1.
La tangente tiene un valor de 0.
Cuando el ángulo es 30º:
El seno tiene un valor de \( \large 1\over 2 \).
El coseno tiene un valor de \( \sqrt {3} \over 2\).
La tangente tiene un valor de \( \sqrt {3} \over 3\).
Cuando el ángulo es 45º:
El seno tiene un valor de \( \sqrt {2} \over 2\).
El coseno tiene un valor de \( \sqrt {2} \over 2\).
La tangente tiene un valor de 1.
Cuando el ángulo es 60º:
El seno tiene un valor de \( \sqrt {3} \over 2\).
El coseno tiene un valor de \( 1\over 2 \).
La tangente tiene un valor de \( \sqrt {3} \).
Cuando el ángulo es 90º:
El seno tiene un valor de 1.
El coseno tiene un valor de 0.
La tangente no existe.
Hasta ahora hemos visto razones trigonométricas entre 0º y 90º (primer cuadrante), pero tomamos ángulos alrededor de toda la circunferencia.
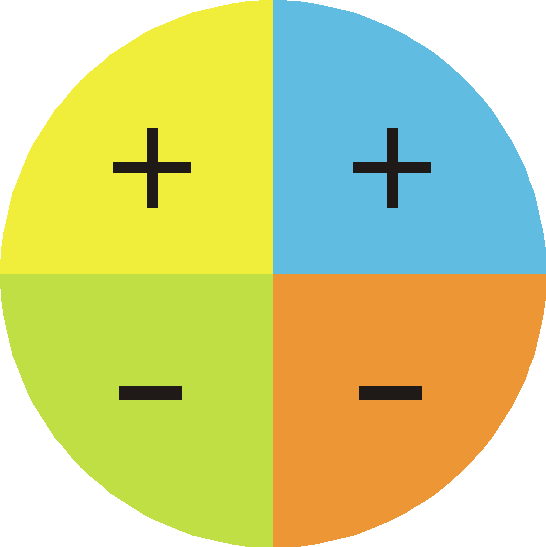
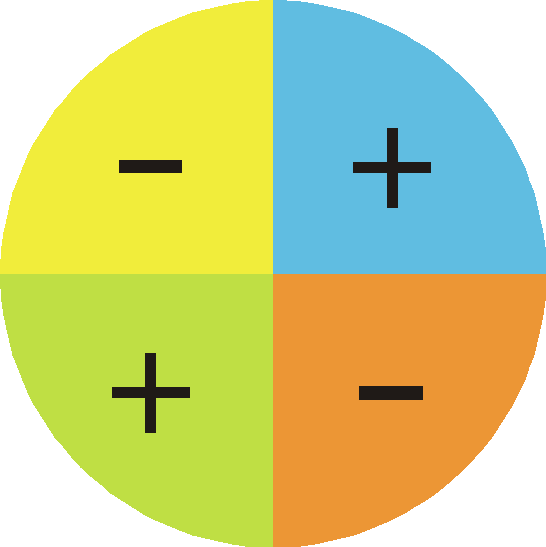
En cada uno de estos cuadrantes, las razones trigonométricas toman valores análogos, pero de signo diferente, en función del segmento que definen sobre los ejes. En la siguiente imagen tienes los signos de cada razón trigonométrica en función del cuadrante:
 |
 |
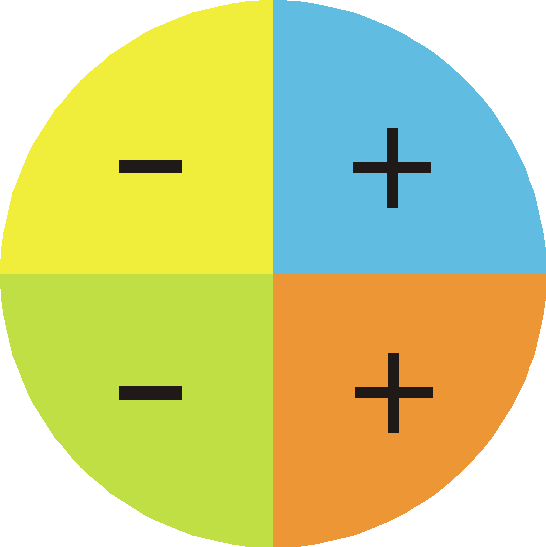 |
| seno | coseno | tangente |

Definición
Tiene la misma función o parecida.
Ejemplo
Los dos círculos son análogos.
Puedes calcular el seno, el coseno y la tangente de cualquier ángulo.
Los ángulos están alrededor de toda la circunferencia.
Divide la circunferencia en cuatro cuadrantes.
En cada uno de los cuadrantes, el seno, el coseno y la tangente
tienen valores parecidos pero de signo diferente.
En esta imagen tienes los signos
para calcular el seno, el coseno y la tangente.
 |
 |
 |
| seno | coseno | tangente |
Las razones trigonométricas de cualquier ángulo pueden relacionarse con otro ángulo del primer cuadrante.
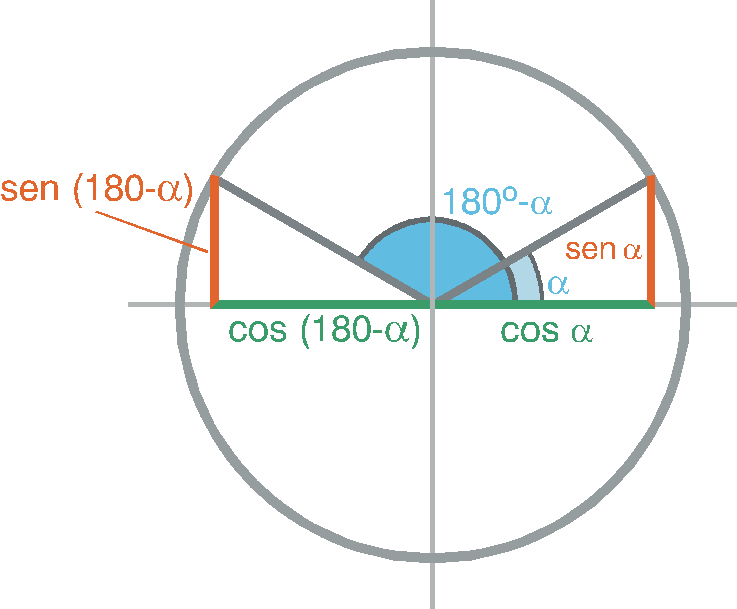
\(sen\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{sen\ \alpha } \)
\(cos\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{-cos\ \alpha } \)
\(tg\ \left ( \ 180 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 180 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{sen\ \alpha }}{\color{red}{-cos\ \alpha }}\ = \ \color{red}{-tg\ \alpha} \)
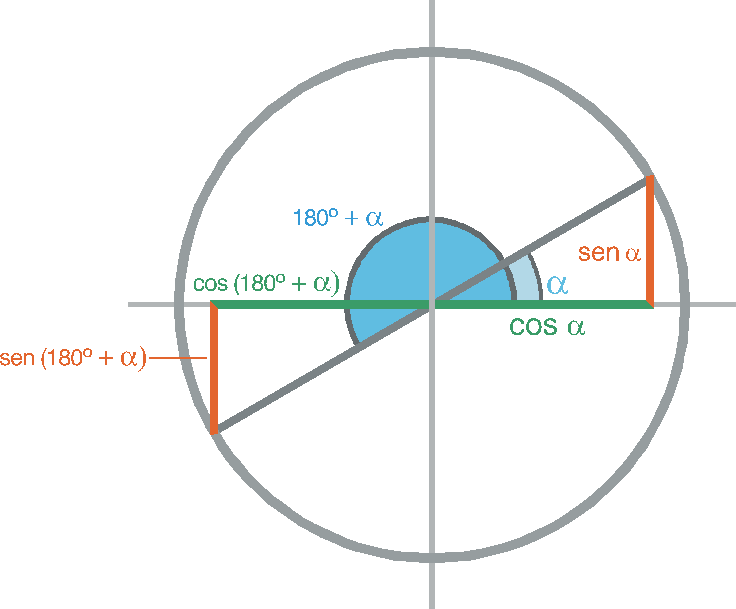
\(sen\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{- sen\ \alpha } \)
\(cos\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{-cos\ \alpha } \)
\(tg\ \left ( \ 180 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 180 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{-sen\ \alpha }}{\color{red}{-cos\ \alpha }}\ = \ \color{red}{tg\ \alpha} \)
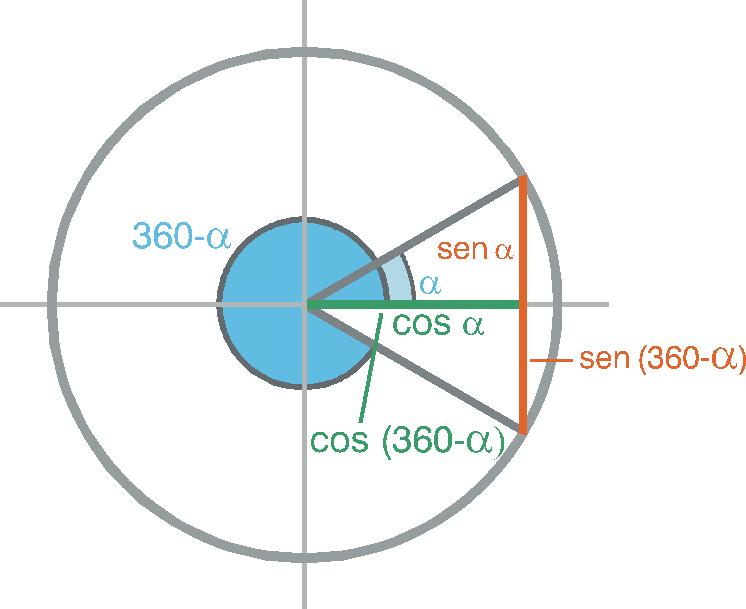
\(sen\ \left( \ 360\ - \ \alpha\ \right) \ = \ \color{red}{- sen\ \alpha } \)
\(cos\ \left( \ 360 \ - \ \alpha\ \right) \ = \ \color{red}{cos\ \alpha } \)
\(tg\ \left ( \ 360 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 360 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{- sen\ \alpha }}{\color{red}{cos\ \alpha }}\ = \ \color{red}{-tg\ \alpha} \)
En el segundo cuadrante de la circunferencia:

\(sen\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{sen\ \alpha } \)
\(cos\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{-cos\ \alpha } \)
\(tg\ \left ( \ 180 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 180 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{sen\ \alpha }}{\color{red}{-cos\ \alpha }}\ = \ \color{red}{-tg\ \alpha} \)
En el tercer cuadrante de la circunferencia:

\(sen\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{- sen\ \alpha } \)
\(cos\ \left( \ 180 \ - \ \alpha\ \right) \ = \ \color{red}{-cos\ \alpha } \)
\(tg\ \left ( \ 180 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 180 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{-sen\ \alpha }}{\color{red}{-cos\ \alpha }}\ = \ \color{red}{tg\ \alpha} \)
En el cuarto cuadrante de la circunferencia:

\(sen\ \left( \ 360\ - \ \alpha\ \right) \ = \ \color{red}{- sen\ \alpha } \)
\(cos\ \left( \ 360 \ - \ \alpha\ \right) \ = \ \color{red}{cos\ \alpha } \)
\(tg\ \left ( \ 360 \ - \ \ alpha\ \right) \ = \frac{sen\ \left( \ 360 \ - \ \alpha\ \right)}{cos\ \left( \ 180 \ - \ \alpha\ \right)} \ = \ \frac{\color{red}{- sen\ \alpha }}{\color{red}{cos\ \alpha }}\ = \ \color{red}{-tg\ \alpha} \)
Resumiendo:
El seno de un ángulo del primer y segundo cuadrante es positivo.
El seno de un ángulo del tercer y cuarto cuadrante es negativo.
El coseno de un ángulo del primer y cuarto cuadrante es positivo.
El coseno de un ángulo del segundo y tercer cuadrante es negativo.
La tangente de un ángulo del primer y tercer cuadrante es positiva.
La tangente de un ángulo del segundo y cuarto cuadrante es negativa.
Cuando representamos el valor de cada razón trigonométrica en función del ángulo, obtenemos una función, periódica que se repite cada 2\(\pi\) radianes o 360º.
Cuando representas el valor del seno, del coseno y de la tangente
en función del ángulo,
obtienes una función periódica que se repite cada 2π radianes o 360º.
La función seno es una función continua y periódica entre 0 y 2 \(\pi\).
Una función continua significa que puede dibujarse de un solo trazo.
Una función periódica significa que se repite el intervalo.
Alcanza un valor de 0 para 0 radianes, comienza a crecer, tomando un valor máximo de 1 para \(\pi\)/2.
La función empieza a disminuir tomando de nuevo un valor de 0 para \(\pi\)
Continúa disminuyendo, alcanzando un valor mínimo de -1 para 3\(\pi\)/2
y comienza a crecer, hasta volver a valer 0 en 2\(\pi\).
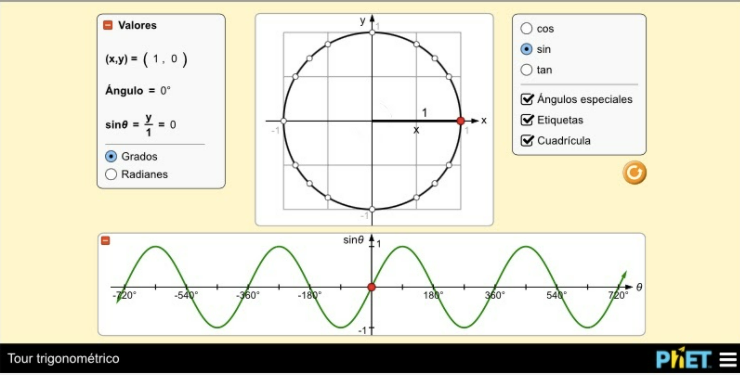
Valores de los ángulos en grados.
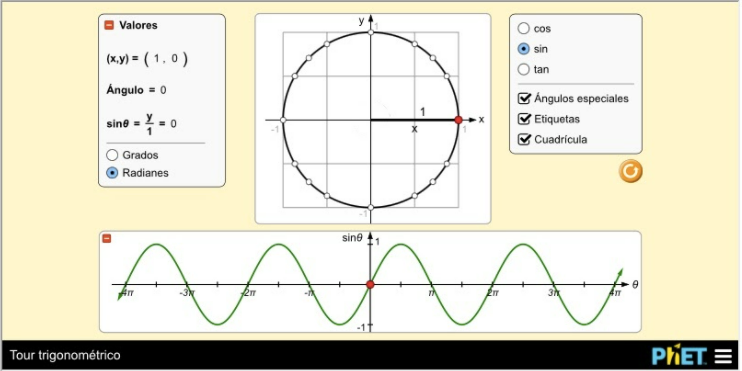
Valores de los ángulos en radianes.
La función coseno es una función continua y periódica entre 0 y 2\(\pi\).
Una función continua significa que puede dibujarse de un solo trazo.
Una función periódica significa que se repite el intervalo.
Alcanza un máximo en 0 radianes, cuyo valor es 1,
disminuye tomando para \(\pi\)/2 un valor de 0.
La función continúa disminuye hasta \(\pi\), que toma un valor de -1,
A partir de \(\pi\) vuelve a crecer, tomando de nuevo el valor 0 para 3\(\pi\)/2
y volver a tomar el valor máximo en 2\(\pi\).
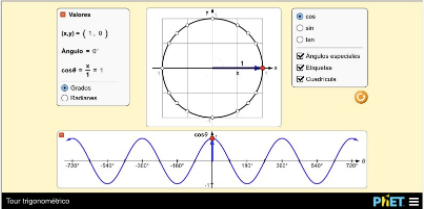
Valores de los ángulos en grados.
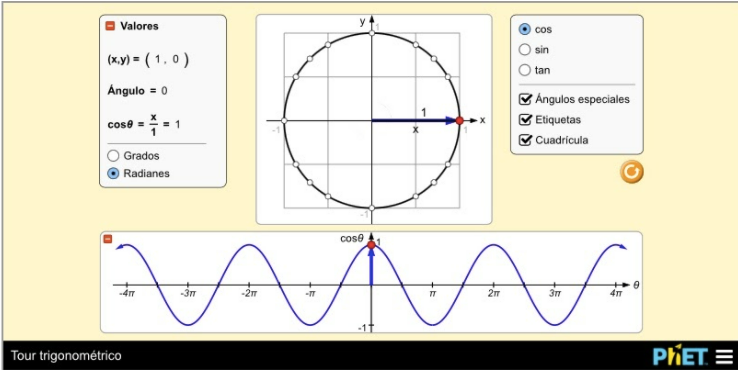
Valores de los ángulos en radianes.
La función tangente es una función discontinua entre -\(\pi\) y \(\pi\).
La función vale 0 en -\(\pi\) radianes, en 0 radianes y en \(\pi\) radianes.
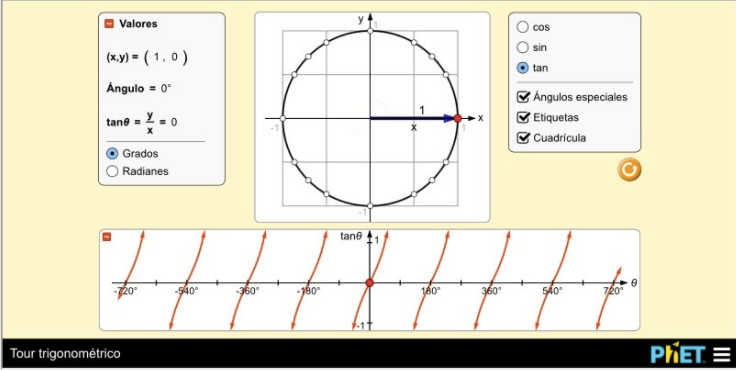
Valores de los ángulos en grados.
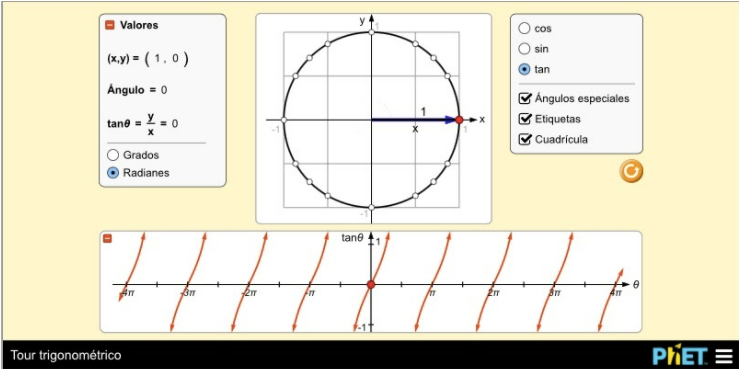
Valores de los ángulos en radianes.
Como hemos visto, el valor de las razones trigonométricas de ángulos del 2º al 4º cuadrante se relacionan con el valor de un ángulo del primer cuadrante.
En esta actividad vas a calcular las razones de ángulos relacionándolos con el valor de un ángulo conocido del primer cuadrante.
Conocidas las razones trigonométricas del ángulo de 30º, calcula las razones de los ángulos de 150º, 210º y 330º.
Usa la simulación anterior para obtener los ángulos anteriores.
Relaciona las razones trigonométricas de los II-IV cuadrantes con los del primero.
Relaciona en tu cuaderno las razones trigonométricas de 150º, 210º y 330º con las del ángulo de 30º.
Tomamos los valores de las razones de este ángulo (ángulo conocido) y calculamos su valor.
El siguiente geogebra te puede ayudar con este ejercicio:
Observa las funciones trigonométricas, obtenidas al representar el valor de cada razón en función del ángulo.
Contesta a estas cuestiones en tu cuaderno para cada una de las razones trigonométricas (seno, coseno, tangente):
Anota en tu cuaderno la relación de las relaciones trigonométricas de cualquier ángulo en relación con las razones del ángulo correspondiente del primer cuadrante.
Elabora una infografía con tus resultados.
Hasta ahora has aprendido nuevas armas y poderes para lograr el reto final.
¡Ánimo! TODAS las personas podemos aprender de TODO.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0