Diccionario

Equivalencias

Circunferencia en la que aparecen la equivalencia entre grados sexagesimales y radianes.

Definición: Igualdad en el valor.
Ejemplo: La equivalencia entre grados sexagesimales y radianes es \( \pi\ =180º\).

1. Convirtiendo ángulos

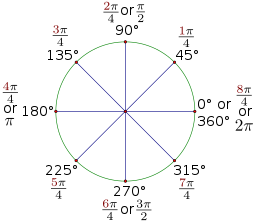
No siempre nos enfrentaremos con ángulos como los anteriores (0º, 90º, 30º, 180º…) de los cuales, de tanto usarlos, nos sabemos sus equivalencias en radianes. En esta actividad debes calcular las equivalencias de ciertos ángulos en grados sexagesimales y viceversa.

Pasar de un tipo de grados a otros lo llamamos también conversión.

Pero antes de empezar debes saber algunas cosas. Te las explicaré con ejemplos:

Si queremos, por ejemplo, pasar un ángulo de 25º a radianes el resultado lo daremos siempre en función de \(\pi\). ¿Qué quiere decir? Pues muy fácil. Observa:

\frac{2\pi}{360} = \frac{x}{25} \quad \to \quad x = \frac{25 \cdot2 \pi}{360}=\frac{50\pi}{360}=\frac{5\pi}{36} rad

Es decir, diremos que 25º son \(\frac{5\pi}{36} rad \). Eso es dejar el resultado en función de \(\pi\).

Y la otra cosa que debes saber es la siguiente.

Cuando pasamos de radianes a grados sexagesimales puede ser que el resultado sea exacto. Por ejemplo: nos piden calcular cuántos grados son 3\(\pi\)/4 radianes.

\frac{2\pi}{360}=\frac{3\pi/4} {x} \quad \to \quad x=\frac {360 \times 3\pi / 4 }{2\pi} = \frac {1080\pi / 4}{2\pi} = \frac{1080\pi}{2\pi \times 4} = 135\ grados

Perfecto. Nos da un número exacto de grados. Pero… ¿y si salen decimales? Haremos lo siguiente. Observa el ejemplo:

\frac{2\pi}{360}\ =\ \frac{1,5\ rad}{x} \quad \to \quad x\ = \frac{360 \times 1,5}{2\pi}\ = \ \frac{540}{2\pi}\ = \ 85,943669\ grados

¿A que queda feo poner tantos decimales? Bueno, pues tu calculadora te dará la solución directamente en grados, minutos y segundos, de manera que des una respuesta más adecuada. Observa cómo hacerlo:

Calculadora pasada a grados, minutos y segundos

O sea, pasarás de ver:

La imagen muestra una calculadora en grados

a ver...

la imagen muestra una calculadora en grados minutos y segundos

Lectura facilitada

Has utilizado muchas veces los ángulos 0º, 90º, 30º, 180º…

Conoces el valor de estos ángulos en radianes.

Calcula los valores de los ángulos en grados sexagesimales.

Calcula los grados sexagesimales en radianes.

Pasar de grados sexagesimales a radianes se llama conversión.

Pasar de radianes a grados sexagesimales se llama conversión.

Por ejemplo, al pasar de grados sexagesimales a radianes,

el resultado se expresa con la unidad π.

Por ejemplo, pasa un ángulo de 25º a radianes.

El resultado se expresa utilizando π.

Observa:

\frac{2\pi}{360} = \frac{x}{25} \quad \to \quad x = \frac{25 \cdot2 \pi}{360}=\frac{50\pi}{360}=\frac{5\pi}{36} rad

El resultado de pasar un ángulo de 25 grados (25º) a radianes

es \(\large\frac{5\pi}{36}\) radianes.

\(\large\frac{5\pi}{36}\) es el resultado expresado en π.

Y la otra cosa que debes saber es la siguiente.

Cuando pasas de radianes a grados sexagesimales

el resultado puede ser exacto.

Exacto significa que es un número que no tiene decimales.

Por ejemplo, calcula cuántos grados son 3\(\pi\)/4 radianes.

\frac{2\pi}{360}=\frac{3\pi/4} {x} \quad \to \quad x=\frac {360 \times 3\pi / 4 }{2\pi} = \frac {1080\pi / 4}{2\pi} = \frac{1080\pi}{2\pi \times 4} = 135\ grados

El resultado de pasar 3\(\pi\)/4 radianes a grados es 135 grados.

135 grados es un número exacto.

Si el resultado fuese un número decimal,

este número decimal puedes transformarlo

a grados, minutos y segundos utilizando la calculadora.

Mira el ejemplo:

\frac{2\pi}{360}\ =\ \frac{1,5\ rad}{x} \quad \to \quad x\ = \frac{360 \times 1,5}{2\pi}\ = \ \frac{540}{2\pi}\ = \ 85,943669\ grados

El resultado es 85, 943669 grados.

85, 943669 es un número decimal.

Cuando el número tiene muchos decimales

utiliza tu calculadora para pasar el numero decimal

a grados, minutos y segundos.

Pulsa en la calculadora la tecla que se indica en la imagen.

Observa cómo hacerlo:

Calculadora pasada a grados, minutos y segundos

Al pulsar la tecla, el número decimal se transformará

en grados, minutos y segundos.

El número que tienes en la calculadora es 85, 943669.

Si pulsas en la tecla que se indica,

este número se transforma en 85º 56´ 37´´.

85 grados, 56 minutos y 37 segundos.

¿Has sentido más seguridad al utilizar la calculadora?

Podrás utilizar la calculadora para convertir los números decimales a grados, minutos y segundos.

¡Ánimo! Al final de este reto encontrarás una calculadora que te puede ayudar.