Diccionario
Cociente
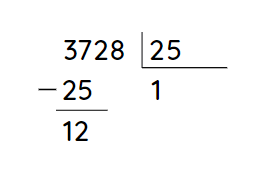
- Definición
-
Resultado de dividir dos números.
- Ejemplo
-
Calcula el cociente de dividir 3728 entre 25.
Constantes

- Definición
-
Elemento que permanece siempre igual.
- Ejemplo
-
La recta es constante.
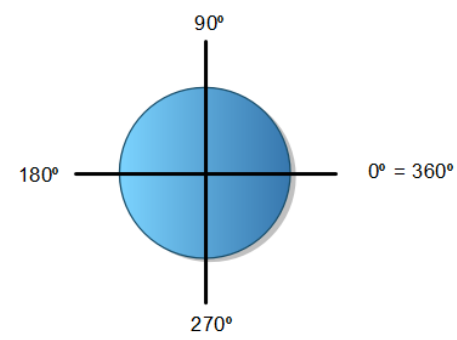
Coordenadas
- Definición
-
Sistema de referencia que utiliza números para saber la posición exacta de un punto.
- Ejemplo
-
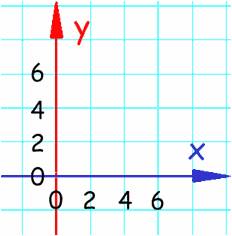
Los ejes de coordenadas con X e Y.
Segmento
- Definición
-
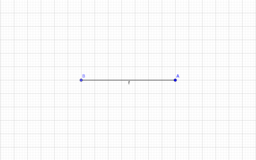
Fragmento de la recta que está comprendido entre dos puntos.
- Ejemplo
-
Dibuja un segmento con la regla.


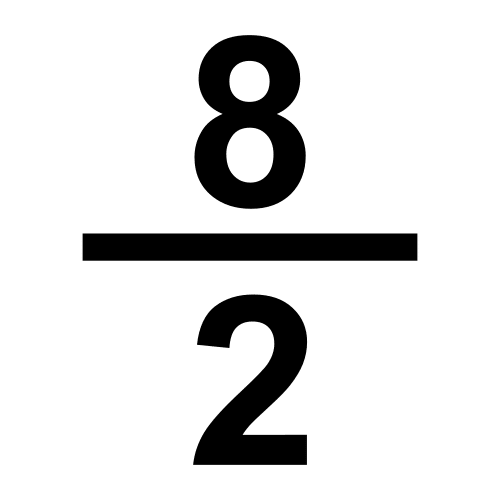

.png)
.png)
.png)
.png)