Paso 1
Descomponemos la inecuación \(x\ -\ 5\ ≤\ 3\ +\ \Large{\frac{x}{3}}\) en dos ecuaciones de rectas.
\(y\ =\ x\ -\ 5 \)
\(y\ =\ 3\ +\ \Large{\frac{x}{3}}\)
Paso 2
Representamos gráficamente las ecuaciones.
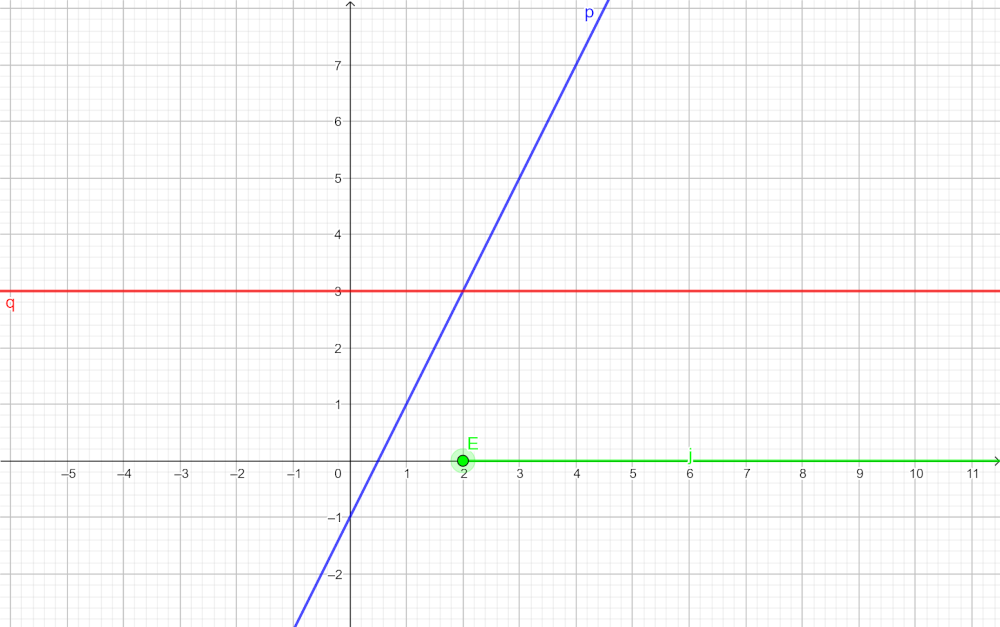
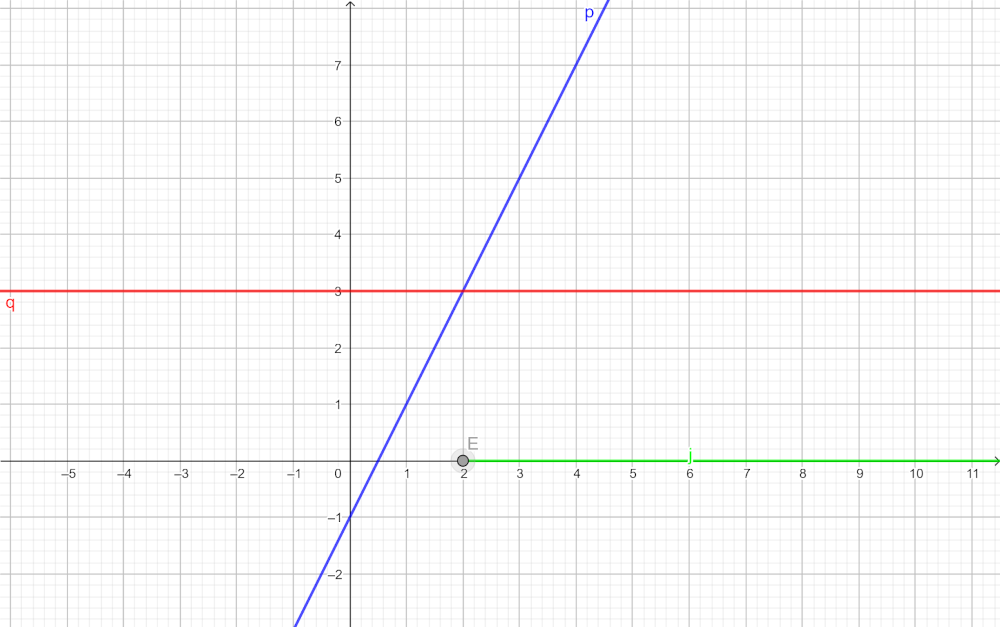
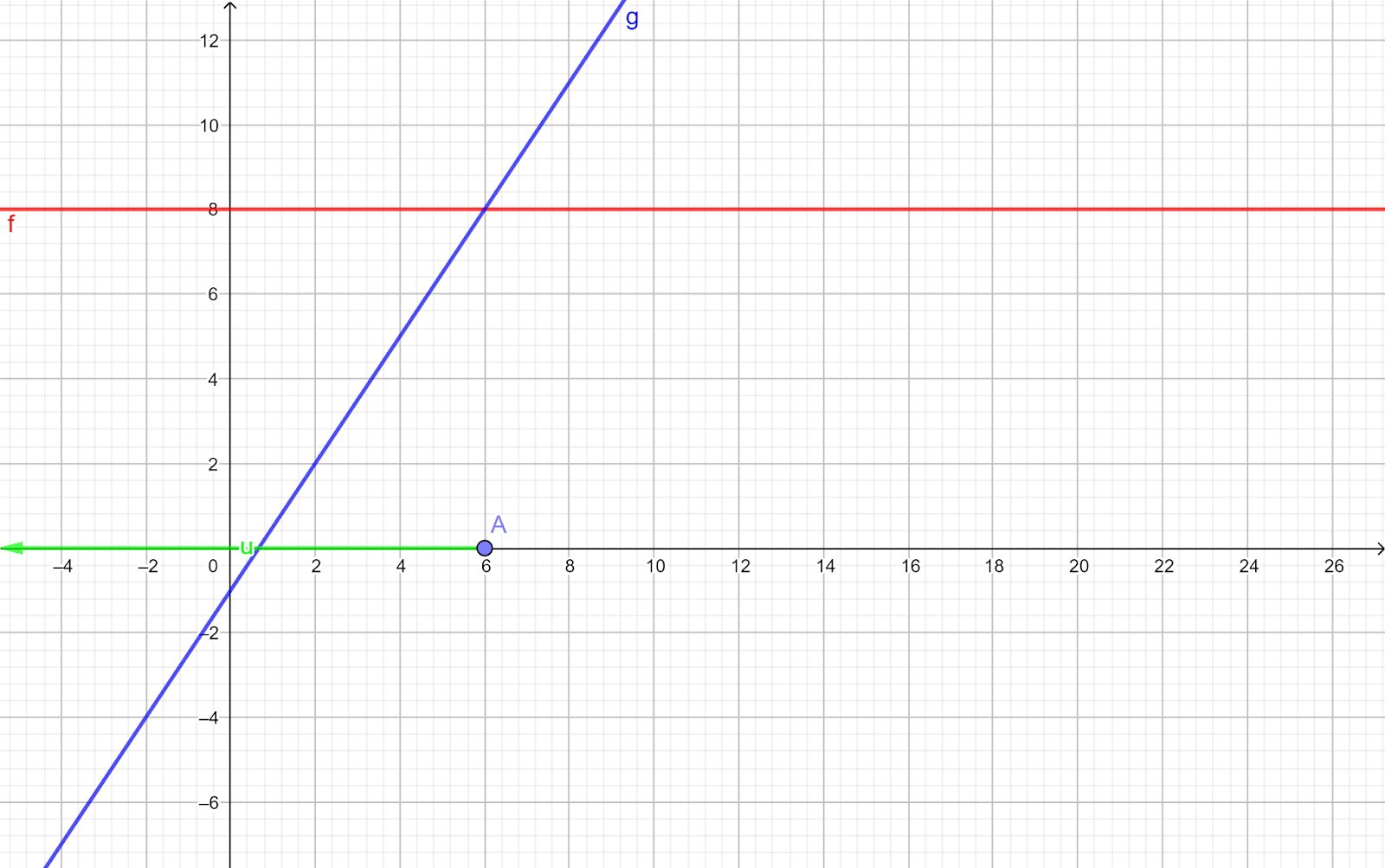
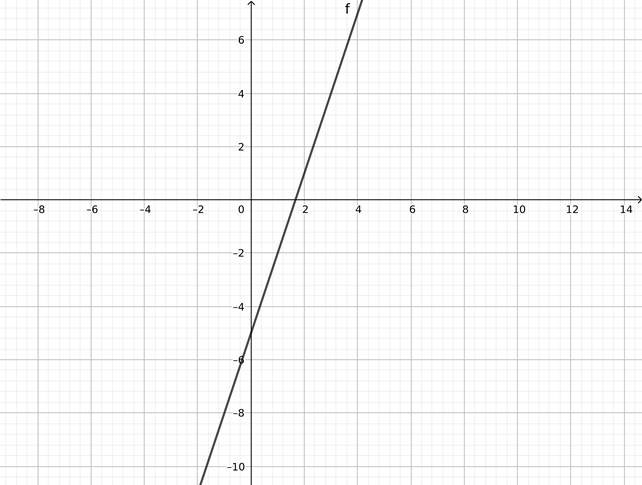
Esta es la representación de \( y\ =\ x\ -\ 5 \).
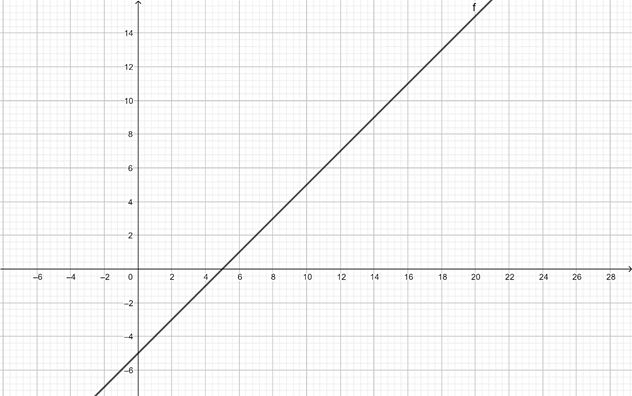
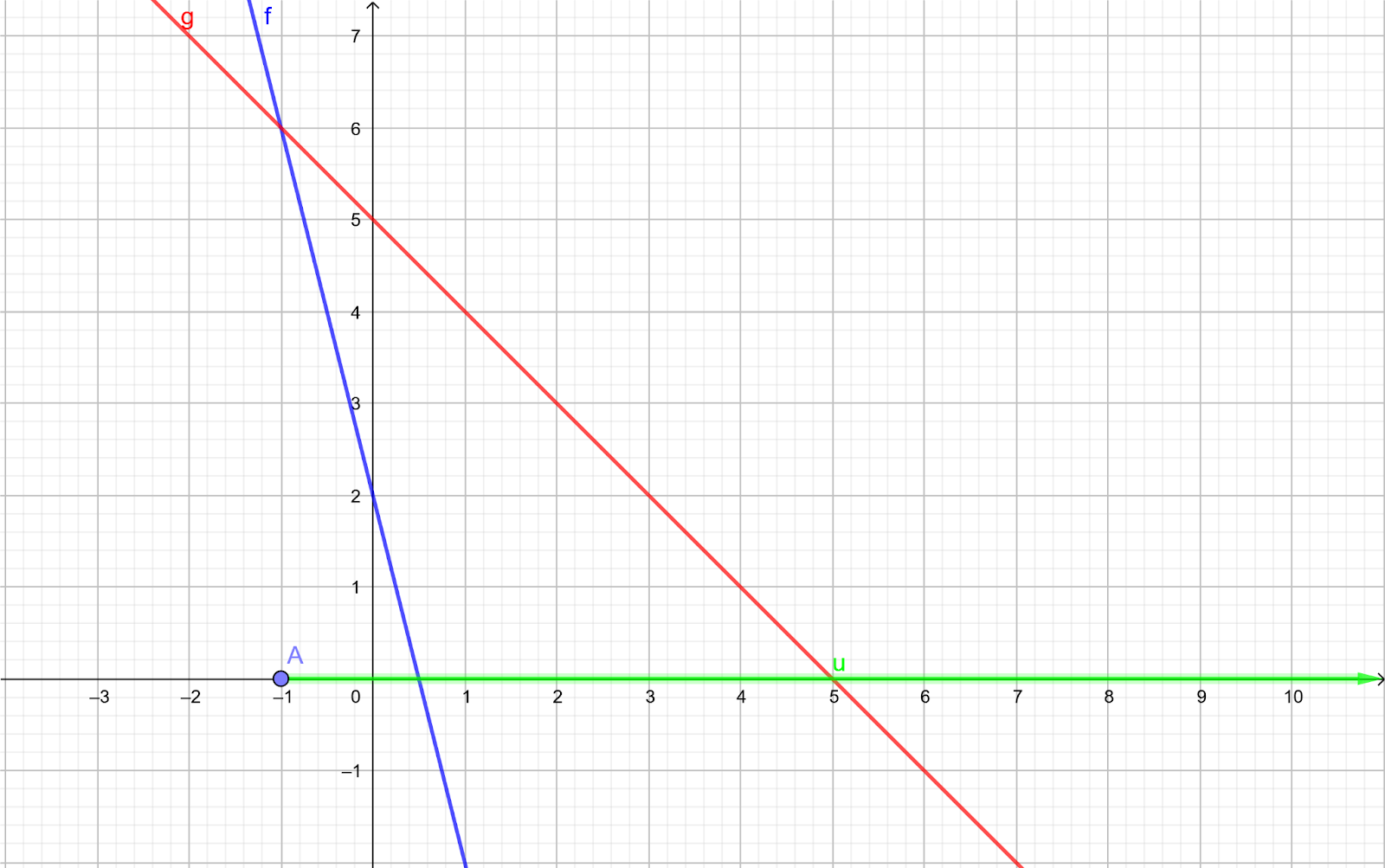
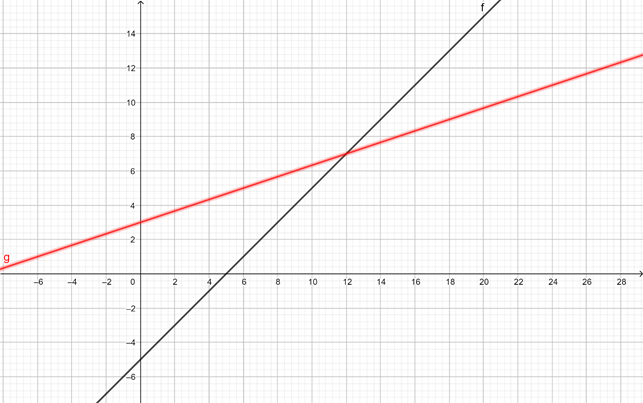
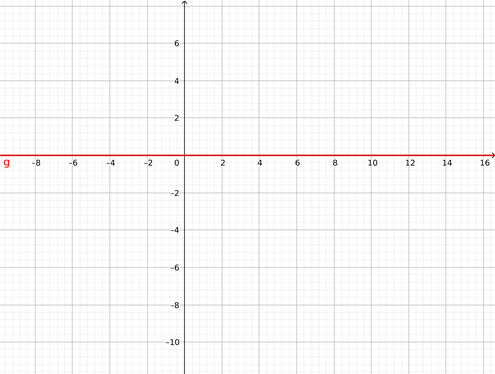
Y esta es la de \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\).
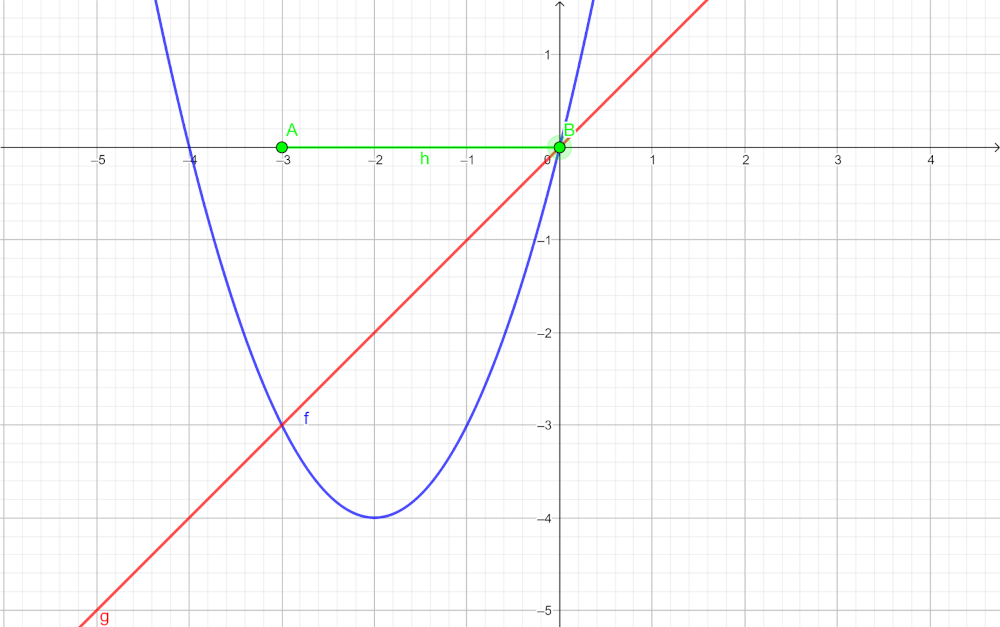
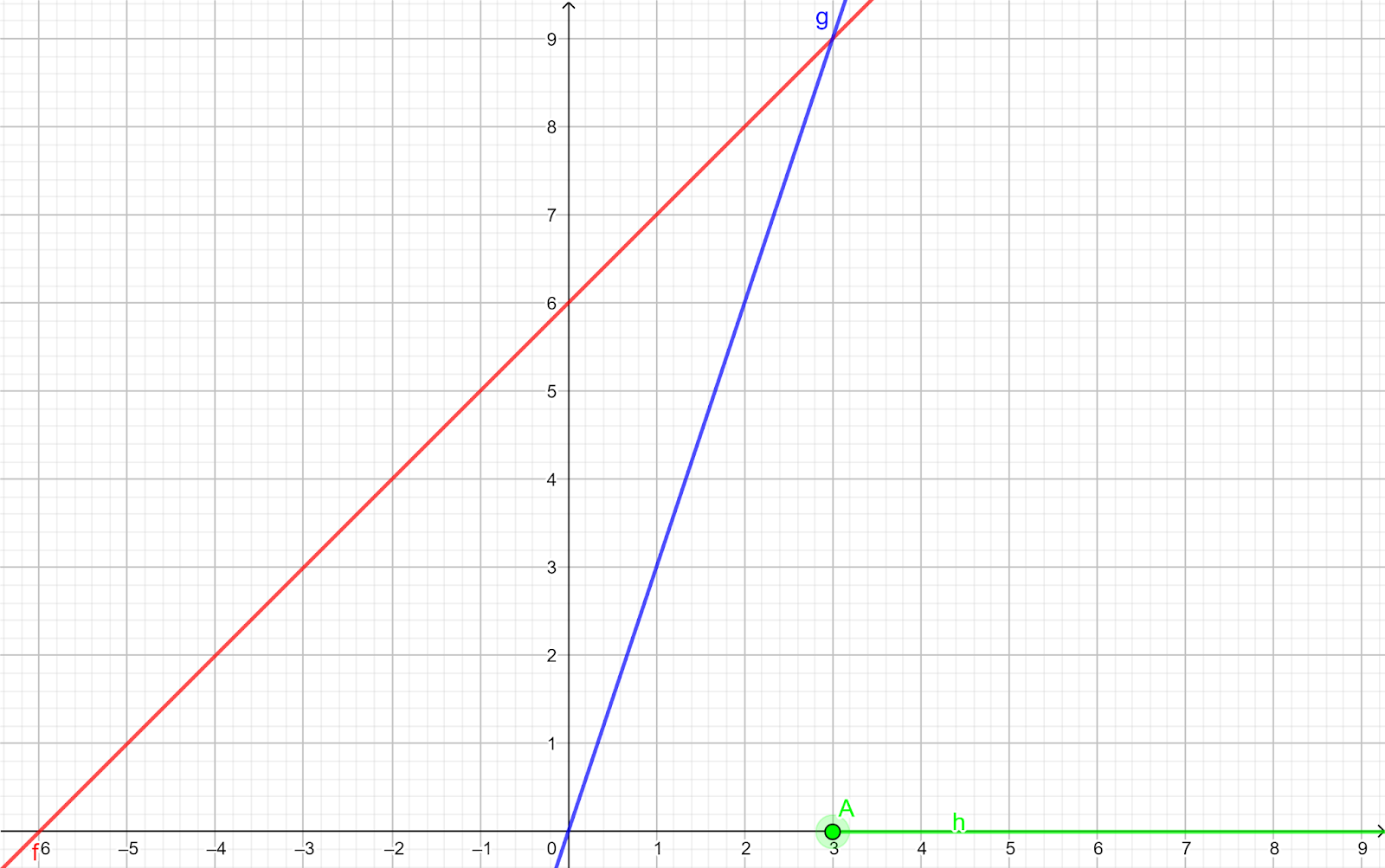
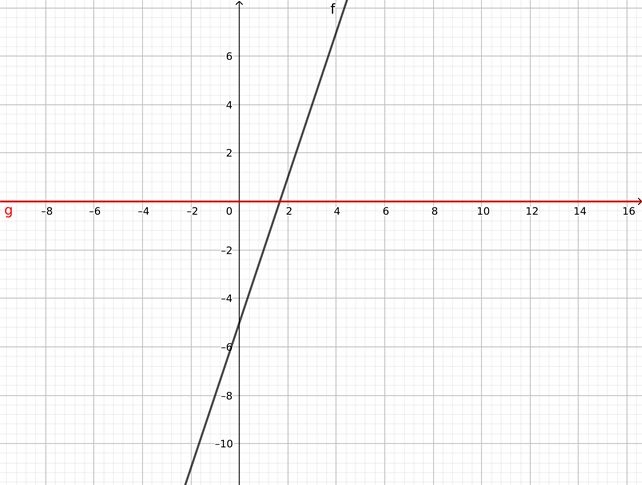
Y aquí tienes las 2 juntas:
Paso 3
Ahora se trata de interpretar lo que nos dicen con la inecuación \(x\ -\ 5\ ≤\ 3\ +\ \Large{\frac{x}{3}}\).
¿No podríamos leerla así?
Buscamos valores de \(x\) para los que \(y\ = \ x\ -\ 5\) esté por debajo de (\(\le\)) \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\).
¿Qué tal si lo leemos ahora de derecha a izquierda?
Buscamos valores de \(x\) para los que \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\) esté por encima de \(y\ =\ x\ -\ 5\).
(\(\le\), ¡Recuerda que estás leyendo de derecha a izquierda!)
Si lo piensas detenidamente, verás que estamos diciendo lo mismo.
Paso 4
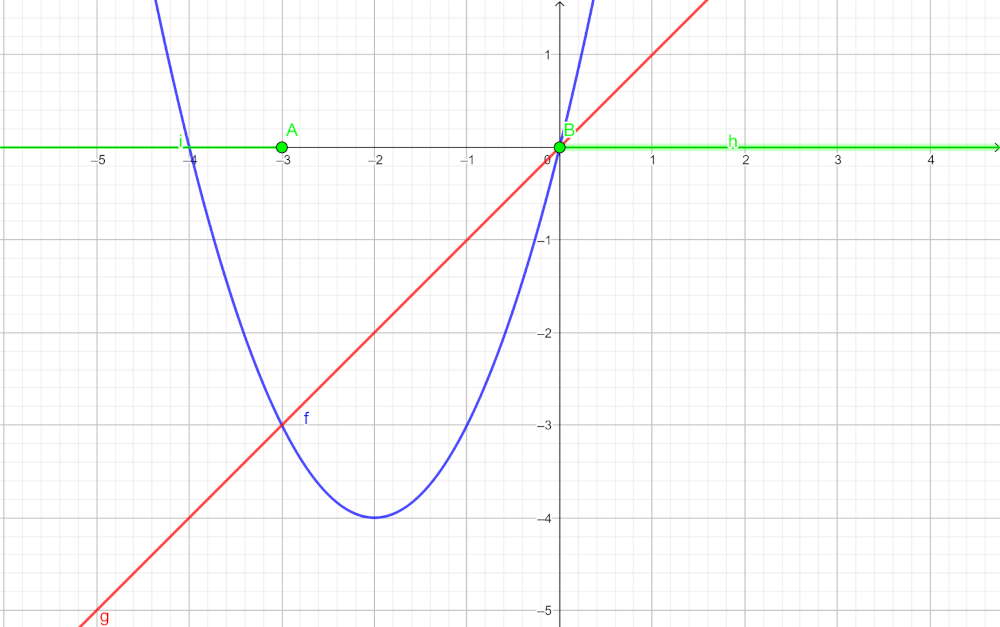
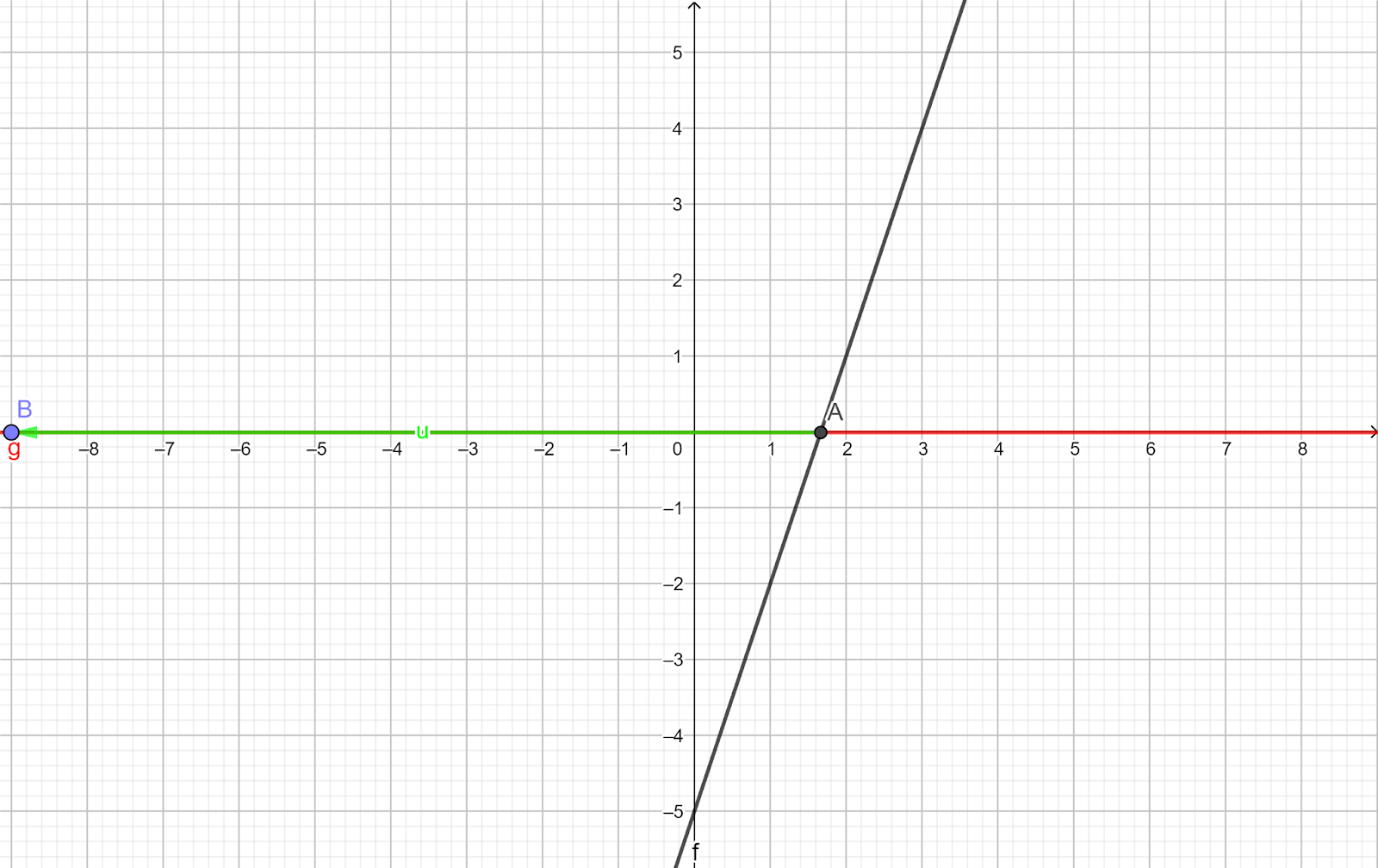
Marcamos los puntos que cumplen con la condición vista en el paso anterior.
¡Ahí van!
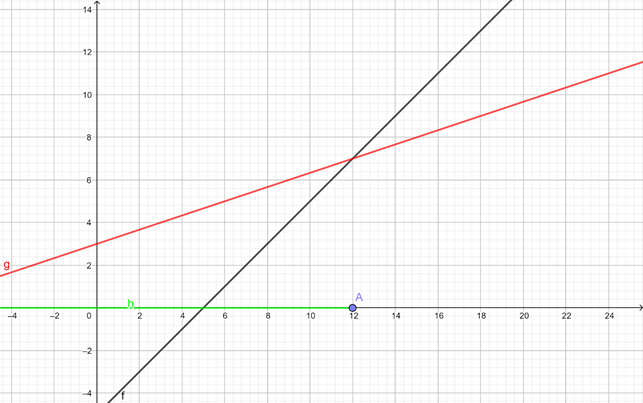
Así es, espero que sea lo que habías pensado. A partir del punto \( A\) hasta el \(-\infty\) la recta \(y\ =\ x\ -\ 5\) está por debajo de \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\).
O lo que es lo mismo, a partir del punto \(A\) hasta el \(-\infty\) la recta \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\) está por encima de \(y\ =\ x\ -\ 5\).
Importante observación: ¿será el punto \(A\) parte de la solución?
Pues claro que sí porque nuestra inecuación es \( x\ -\ 5\ ≤\ 3\ +\ \Large{\frac{x}{3}}\).
Fíjate en que el símbolo \(\le\) contiene el signo igual, por lo que también nos vale el punto en el que \(y\ =\ x\ -\ 5\) es igual que \(y\ =\ 3\ +\ \Large{\frac{x}{3}}\).
Finalmente escribamos la solución en forma de intervalo.
Las soluciones válidas son todos los valores de \( x\) que están en el intervalo \((-\infty\ ,\ 12\ ]\).
O expresado matemáticamente: \( x\ \in (- \infty\ ,\ 12\ ]\).


 Definición
Definición
 Definición
Definición