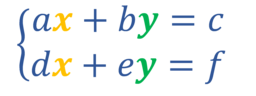Algunas de las cosas que podemos hacer para obtener sistemas equivalentes son:
- Multiplicar o dividir una de las ecuaciones por un número (distinto de cero, claro).
- Sumar o restar las ecuaciones y sustituir el resultado por una de ellas.
- Sumar o restar una expresión algebraica a una de las ecuaciones.
- Cambiar el orden de las ecuaciones.
Esta es la base de la resolución de los sistemas, trabajar con sistemas equivalentes, aunque a la hora de sistematizarlos le ponemos diferentes nombres.
Método de reducción
Como hemos visto, Numeria le ha estado enseñando a Piñonate, que "jugar" con las ecuaciones de un sistema es muy interesante ya que así generamos nuevos sistemas (sistemas equivalentes) y podemos resolver el sistema que más nos convenga, la cuestión es: ¿cuál nos conviene? Nos convendrá siempre el que una de las ecuaciones pierda una incógnita. Vamos a ver en qué consiste el método de reducción.
Recuerda entonces que aunque veamos diferentes métodos, lo importante es que utilizamos sistemas equivalentes para resolver el sistema. Pasos a seguir:
- Multiplicar las ecuaciones por los números adecuados para que los coeficientes de una de las incógnitas sean iguales u opuestos.
-
$\left \{ \begin{array}{rcl} 2x-y&=&-3\\ 3x+2y&=&-4 \end{array} \right. \Longrightarrow$ Multiplicamos la 1º ecuación por 2 $ \Longrightarrow \left \{ \begin{array}{rcl} 4x-2y&=&-6\\ 3x+2y&=&-4 \end{array} \right.$
- Sumar o restar las ecuaciones obtenidas para eliminar la incógnita con coeficientes iguales u opuestos.
-
Sumamos en el anterior sistema para que se nos vayan las y me quedaría, por ejemplo, $\Longrightarrow \left \{ \begin{array}{rcl} 7x&=&-10\\ 3x+2y&=&-4 \end{array} \right.$
- Obtener el valor de una incógnita.
-
En el caso anterior, obtenemos el valor de la incógnita x $\Longrightarrow \left \{ \begin{array}{rcl} x&=&\frac{-10}{7}\\ 3x+2y&=&-4 \end{array} \right.$
- Se sustituye el valor de la incógnita que sabemos en una de las ecuaciones iniciales para obtener el valor de la incógnita que desconocemos.
-
$\left \{ \begin{array}{rcl} x&=&\frac{-10}{7}\\ 3 \cdot \frac{-10}{7} +2y&=&-4 \end{array} \right. \Longrightarrow \left \{ \begin{array}{rcl} x&=&\frac{-10}{7}\\ y&=&\frac{1}{7} \end{array} \right.$ OJO, recuerda de nuevo que la solución de un sistema son dos valores, una para la x y otro para la y.
Practicar el método de reducción...
Método de sustitución
Numeria sigue contándole a Piñonate que entonces, todos los métodos que a continuación se exponen, no son más que otras formas de conseguir los mismo, reducir incógnitas hasta conseguir quedarse con una sola ecuación y una sola incógnita. Vamos a ver cómo sería el método de sustitución.
- Despejamos una incógnita en una de las dos ecuaciones.
-
$\left \{ \begin{array}{rcl} 2x-y&=&-3\\ 3x+2y&=&-4 \end{array} \right. \Longrightarrow$ Por ejemplo, me llevo la y de la 1º ecuación al 2º miembro. $\Longrightarrow \left \{ \begin{array}{rcl} 2x+3&=&y\\ 3x+2y&=&-4 \end{array} \right.$
- Sustituimos ahora la incógnita despejada en la otra ecuación.
-
$\left \{ \begin{array}{rcl} 2x+3&=&y\\ 3x+2(2x+3)&=&-4 \end{array} \right.$
- Resolvemos la ecuación obtenida.
-
$\left \{ \begin{array}{rcl} 2x+3&=&y\\ 7x&=&-10 \end{array} \right. \Longrightarrow \left \{ \begin{array}{rcl} 2x+3&=&y\\ x&=&\frac{-10}{7} \end{array} \right. $
- Sustituimos el valor de la incógnita conocida en una ecuación inicial para calcular la otra incógnita.
-
$\left \{ \begin{array}{rcl} 2\cdot(\frac{-10}{7})+3&=&y\\ x&=&\frac{-10}{7} \end{array} \right. \Longrightarrow \left \{ \begin{array}{rcl} x&=&\frac{-10}{7}\\ y&=&\frac{1}{7} \end{array} \right. $
Como has podido comprobar, Piñonate, esencialmente es igual que antes, queremos usar un sistema equivalente al primero pero que nos interese más trabajar con él. En este método, lo que hacemos es despejar de una de las ecuaciones una de las incógnitas y sustituirla en otra ecuación.
Practicar el método interactivamente...
Método de igualación
Último de los métodos que podemos llamar "algebraicos" para resolver los sistemas lineales de dos incógnitas. El método de igualación, que consiste en despejar de ambas ecuaciones la misma incógnita e igualar para así quedarnos de nuevo con una ecuación con una sólo incógnita, pero que hace que el sistema creado sea equivalente de nuevo. Vamos a verlo en un ejemplo, Piñonate:
- Se elige una de las incógnitas y se despeja de ambas ecuaciones.
-
$\left \{ \begin{array}{rcl} 2x-y&=&-3\\ 3x+2y&=&-4 \end{array} \right. \Longrightarrow$ Escojo por ejemplo la y. $\Longrightarrow \left \{ \begin{array}{ccc} 2x+3&=&y\\ y&=& \large \frac{-4-3x}{2} \end{array} \right.$
- Se igualan los miembros que no tienen la incógnita despejada.
-
$\left \{ \begin{array}{ccc} 2x+3&=&y\\ y&=&\large \frac{-4-3x}{2} \end{array} \right. \Longrightarrow$ Me quedo por ejemplo con la 1ª ecuación. $\Longrightarrow \left \{ \begin{array}{ccc} y&=&2x+3\\ 2x+3&=&\large \frac{-4-3x}{2} \end{array} \right.$
- Resuelvo el valor de la ecuación para obtener el valor de la incógnita.
-
$\left \{ \begin{array}{ccc} y&=&2x+3\\ 2x+3&=&\large \frac{-4-3x}{2} \end{array} \right. \Longrightarrow \left \{ \begin{array}{ccc} y&=&2x+3\\ 4x+6&=&-4-3x \end{array} \right. \Longrightarrow \left \{ \begin{array}{ccc} y&=&2x+3\\ 7x&=&-10 \end{array} \right. \Longrightarrow \left \{ \begin{array}{ccc} y&=&2x+3\\ x&=&\large \frac{-10}{7} \end{array} \right.$
- Sustituyo el valor de la incógnita hallada en la ecuación inicial para obtener el valor de la que no conocemos.
-
$\left \{ \begin{array}{ccc} y&=&2x+3\\ x&=&\large \frac{-10}{7} \end{array} \right. \Longrightarrow \left \{ \begin{array}{ccc} y&=&2 \cdot \large \frac{-10}{7}+3\\ x&=&\large \frac{-10}{7} \end{array} \right. \Longrightarrow \left \{ \begin{array}{rcl} y&=&\large \frac{1}{7}\\ x&=&\large \frac{-10}{7} \end{array} \right. $
Practicar el método de igualación...
Método gráfico
El método más visual para resolver los sistemas de ecuaciones lineales con dos incógnitas, desde luego que es el método gráfico. Vamos a representar gráficamente cada una de las ecuaciones que me dan en un sistema. Recuerda, Piñonate, que son dos líneas rectas. Teniendo en cuenta el último método visto, llamado de igualación, ¿cómo podremos averiguar la solución? Efectivamente, será el punto que cumpla que está en la dos rectas (si es que existe claro). Vamos a seguir con nuestro ejemplo pero ahora lo resolvemos gráficamente.
$\left \{ \begin{array}{rcl} 2x-y&=&-3\\ 3x+2y&=&-4 \end{array} \right.$
|
Representamos gráficamente la 1ª ecuación:
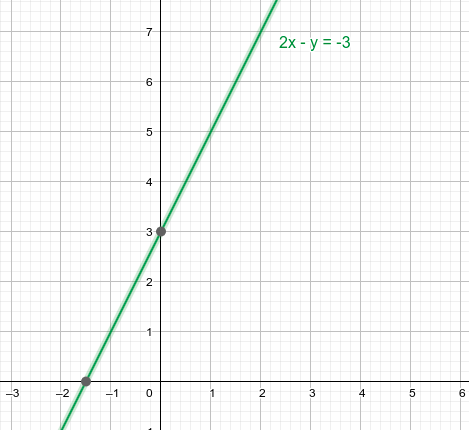
|
Representamos gráficamente la 2ª ecuación:
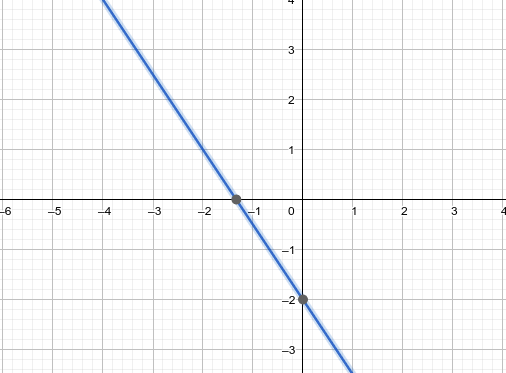
|
Representación de las dos ecuaciones a la vez:
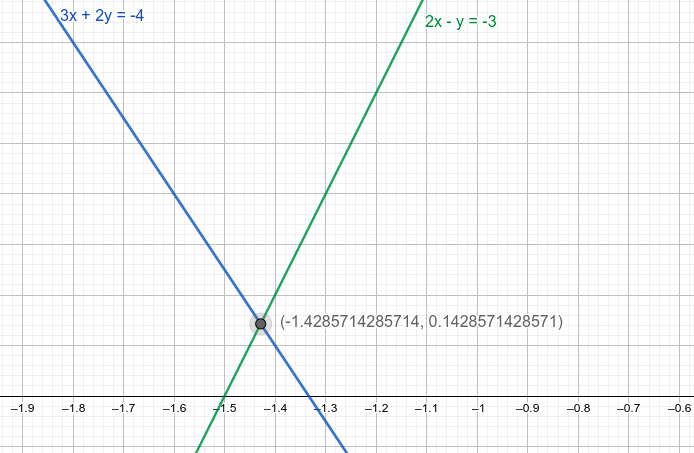
|
La solución del sistema es el punto de corte de las dos rectas. Puedes comprobarlo con las soluciones que hemos ido obteniendo con los otros métodos. También es fácil representarlas y viendo lo que da con la aplicación web Geogebra.org.
Método numérico
Es lo que usualmente podemos llamar por tanteo, Piñonate. No es un método muy usual, quizás por el sentimiento generalizado de que los problemas que se resuelven en matemáticas tienen que tener una solución exacta, sin embargo puede ser útil. (Guía didáctica RECORDAR poner aproximación a las funciones)
Fíjate, Piñonate, en el problema que tenemos con la factura del teléfono. Tenemos que elegir una de los dos compañías y no sabemos cuál de ellas nos conviene más. La compañía Telefinka nos cobra una cantidad fija de 25€ al mes aunque no realicemos llamadas y luego cada llamada a 0,01€ el minuto. La compañía Asustel, nos cobra a 0,05€ el minuto sin ninguna cantidad fija al mes. ¿Nos conviene más Telefinka o Asustel? Vamos a hacer una tabla para verlo:
| Asustel |
| Número de minutos |
€ que tenemos que pagar |
| 1 |
0,3 |
| 5 |
0,25 |
| 10 |
0,5 |
| Vemos que tardan mucho en acercarse. Aumentamos |
| 100 |
5 |
| Seguimos |
| 300 |
15 |
| 400 |
20 |
| 600 |
30 |
| 650 |
32,5 |
| Asustel está por encima de Telefinka |
| 630 |
31,5 |
| Telefinka |
| Número de minutos |
€ que tenemos que pagar |
| 1 |
25,01 |
| 5 |
25,05 |
| 10 |
25,1 |
| Vemos que tardan mucho en acercarse. Aumentamos |
| 100 |
26 |
| Seguimos |
| 300 |
28 |
| 400 |
29 |
| 600 |
31 |
| 650 |
31,5 |
| Asustel está por encima de Telefinka |
| 630 |
31,3 |
Podríamos haber multiplicado la primera ecuación por 3 y la segundo por 2 por ejemplo. Las posibilidades son infinitas, pero buscamos lo más "sencillo"
En este caso he quitado la primera ecuación y la he sustituido por la nueva manteniendo la 2ª ecuación. Podría haberme quedado con la 1ª ecuación y sustituir la 2ª.
Le cambio el orden a los miembros, no pasa nada. Eso lo puedo hacer siempre.
Podríamos seguir afinando, pero a partir de aquí ya podríamos saber a qué compañía nos conviene más apuntarnos realizando un número determinado de minutos en llamadas.


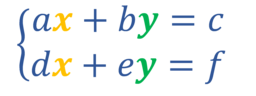


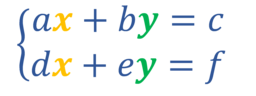 Definición
Definición