Gráfica
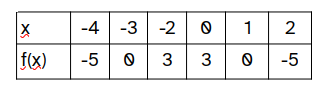
Vamos a ver cómo es la gráfica de una función cuadrática, consideremos la función $f(x)=x²$
Creamos una tabla de valores para que nos oriente sobre cómo será la representación gráfica de la función, en esa tabla pondremos algunos valores que nos orientarán
sobre el comportamiento de la función.
| $x$ |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
| $f(x)=x²$ |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
16 |
Una vez que representamos los puntos de la tabla, los unimos para conocer el comportamiento de la gráfica.
Los puntos que se han tomado se han elegido arbitrariamente, si se toman otros puntos se obtiene la misma gráfica.
A la gráfica de una función cuadrática se le llama parábola.
Pero ¿todas la gráficas de la funciones cuadráticas son así?
Consideremos otra función $f(x)=x²-6x+5$ y procedamos igual
| $x$ |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
| $f(x)=x²-2x-3$ |
21 |
12 |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
Como se pude observar los dos gráficas tienen una forma "similar".
Curvatura
Cabría preguntarse si la gráfica de la función cuadrática, la parábola, tiene siempre la misma forma o depende de alguna característica.
Observa las siguientes parábolas junto a su expresión analítica
Observa como en la primera y en la tercera gráfica el coeficiente de $x^2$ es positivo, mientras que en la tercera es negativo. La forma de la gráfica de la función cuadrática, la parábola, está condicionada por el coeficiente del término de segundo grado.
Se puede conocer la forma que tendrá la gráfica de una función cuadrática observando el coeficiente del término de segundo grado:
- $f(x)=3x²-12$ como el coeficiente del término de segundo grado es 3 que es positivo la gráfica será convexa
- $f(x)=-2x²+x+6$, en este caso el coeficiente es -2, al ser negativo, la gráfica será cóncava
Corte con los ejes
Cuando se representa gráficamente una función cuadrática es importante conocer en qué momento la gráfica corta a los ejes coordenados. Recordemos que la expresión analítica es $f(x)=ax²+bx+c$ y que los puntos de la gráfica tienen por coordenadas $(x,f(x))$
Corte con el eje de ordenadas (eje Y)
En el punto de corte con el eje de ordenadas, $x=0$ y por tanto el punto de corte será $(0,f(0))$. Veamos cuanto vale $f(0)$.
$f(0)=a·0²+b·0+c \Rightarrow f(0)=c$. Luego el punto de corte con el eje de ordenadas es $(0,c)$.
Corte con el eje de abscisas (eje X)
Cuando la función corta al eje de abscisas $f(x)=0$. Por tanto $ax²+bx+c=0$, se plantea una ecuación de segundo grado, las soluciones de esa ecuación serán la primera coordenada de los puntos de corte. Recordemos que las ecuaciones de segundo grado pueden tener dos, una o ninguna solución, luego la gráfica de la función cuadrática puede tener dos puntos de corte con el eje de abscisas, uno o ninguno.
Ejemplo:
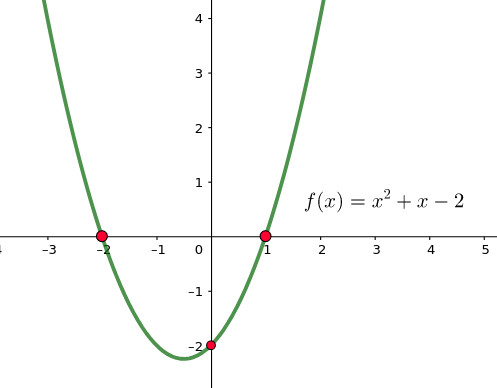
Determina los puntos de corte de $f(x)=x²+x-2$ con los ejes coordenados.
Corte con el eje de ordenadas ($x=0$).
$f(0)=0²+0-2=-2$ luego el punto de corte con el eje de ordenadas es $(0,-2)$.
Corte con el eje de abscisas ($f(x)=0$).
$f(x)=0 \Rightarrow x²+x-2=0$. Resolvemos la ecuación de segundo grado para determinar los puntos de corte \(x=\dfrac{-b\pm \sqrt{b²-4ac}}{2a} \).
En nuestra ecuación $a=1$, $b=1$, $c=-2$
\(x=\dfrac{-b\pm \sqrt{b²-4ac}}{2a} \Rightarrow x=\dfrac{-1 \pm \sqrt{1²-4·1·(-2)}}{2·1} \Rightarrow x=\dfrac{-1 \pm 3}{2}\) $x_1=\dfrac{-1+3}{2}=1$ y $x_2=\dfrac{-1-3}{2}=-2$. La gráfica de la función corta al eje de abscisas en los puntos $(-2,0)$ y $(1,0)$
Vértice
Hay un punto singular en toda representación de una parábola y es su vértice.
- Si la gráfica es convexa, el vértice coincide con el mínimo.
- Si la gráfica es cóncava,, el vértice coincide con el máximo.
Cálculo del vértice
$V=\left( \dfrac{-b}{2a},f \left(\dfrac{-b}{2a} \right) \right)$
Ejemplo:
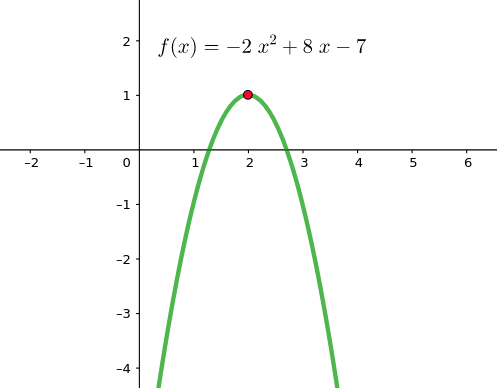
Determina el vértice de $f(x)=-2x²+8x-7$
$V=\left( \dfrac{-b}{2a},f \left(\dfrac{-b}{2a} \right) \right)=\left(\dfrac{-8}{2·(-2)},f \left(\dfrac{-8}{2·(-2)} \right) \right)=(2,f(2))$
$f(2)=-2·2²+8·2-7=1$. Luego el vértice tiene coordinadas (2,1).
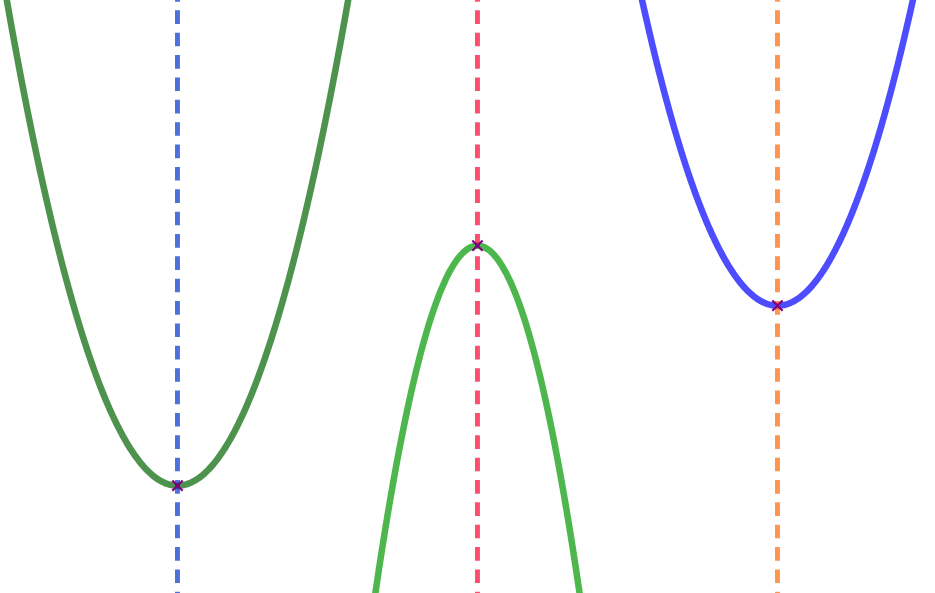
Simetría
Observa las gráficas, en ellas se muestran tres parábolas. ¿Serías capaz de trazar una recta que dividiese cada parábola en dos partes iguales?
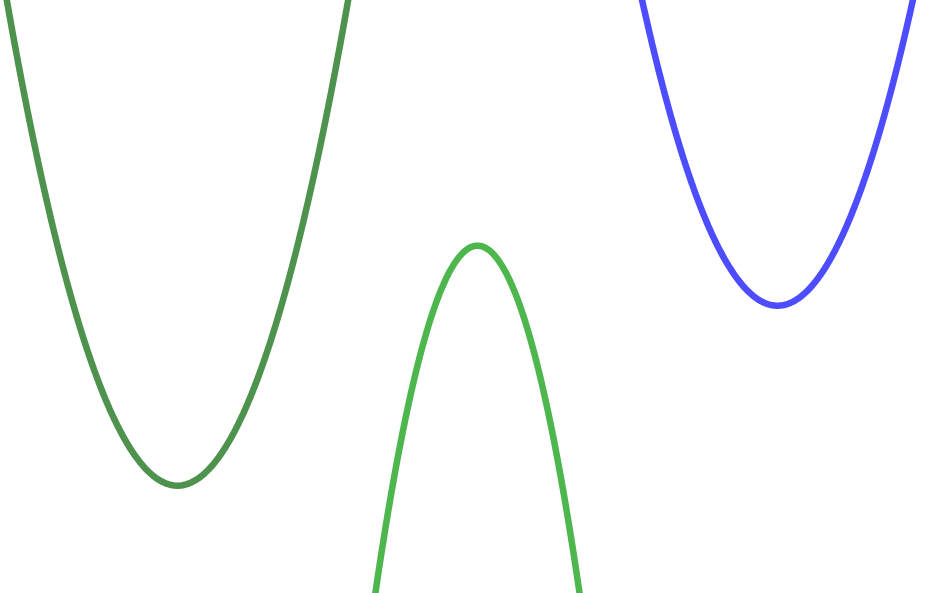
Si has conseguido hacerlo esa recta es el eje de simetría de la parábola. Todas las parábolas tienen un eje de simetría y coincide con la recta vertical $x=\dfrac{-b}{2a}$
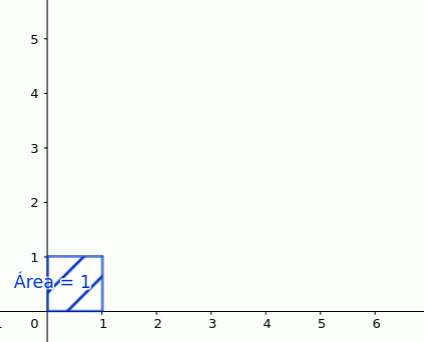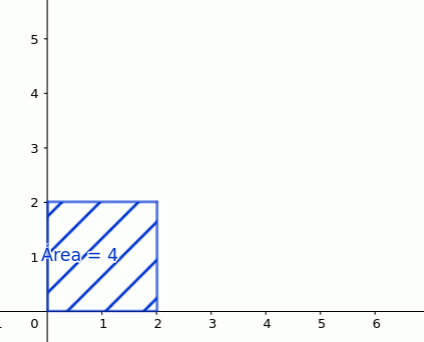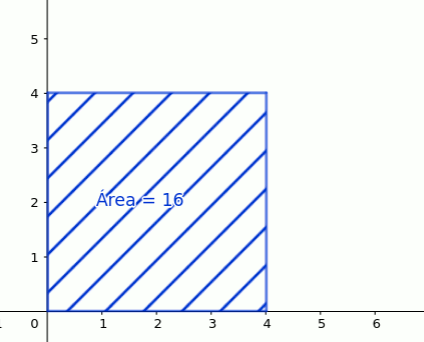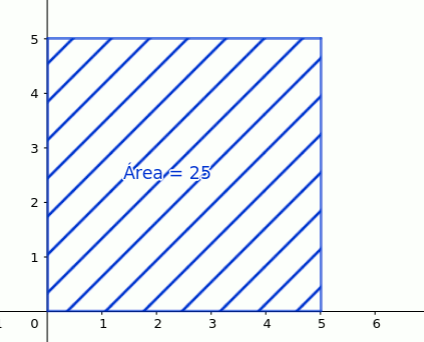Queremos conocer la relación entre el lado de un cuadrado y su área.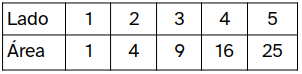 
Hemos hablado de la energía solar fotovoltaica en los apartados anteriores pero cabe preguntarse ¿hay alguna otra forma de obtener electricidad del sol?.