Autoría


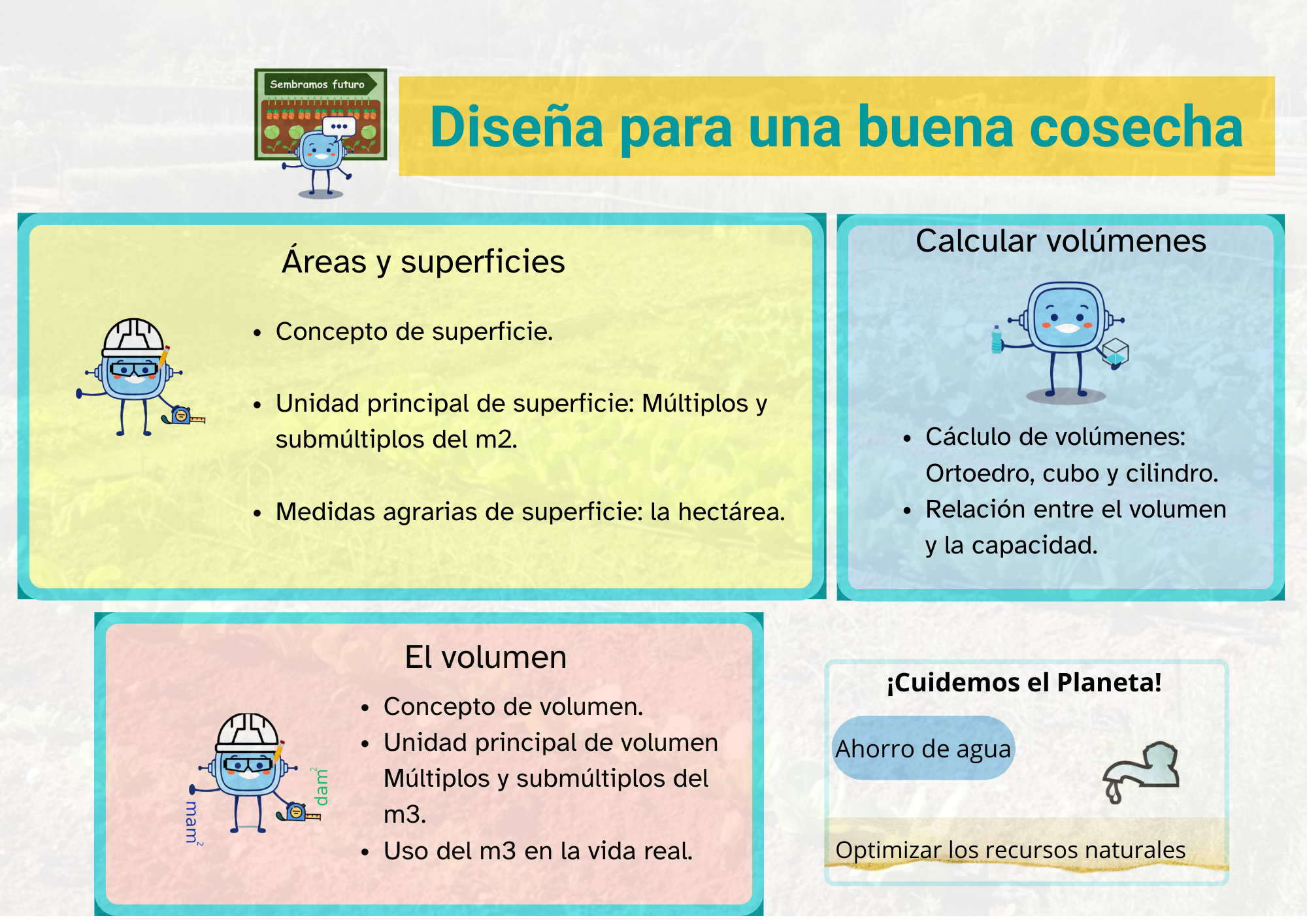
Título	Diseña para una buena cosecha
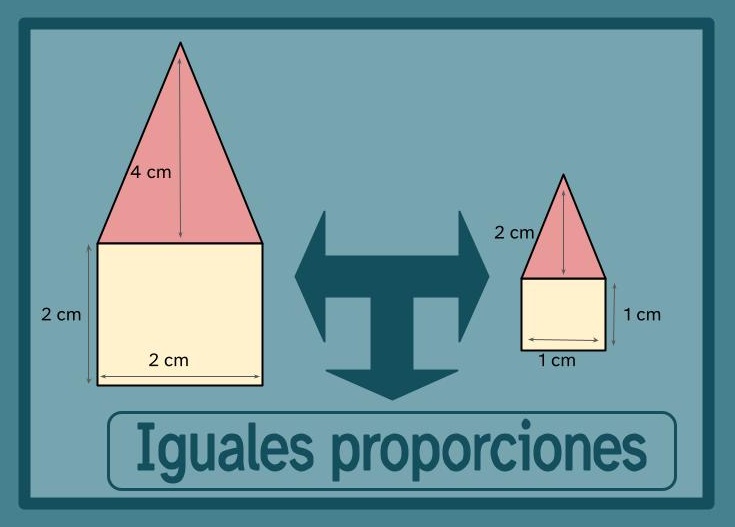
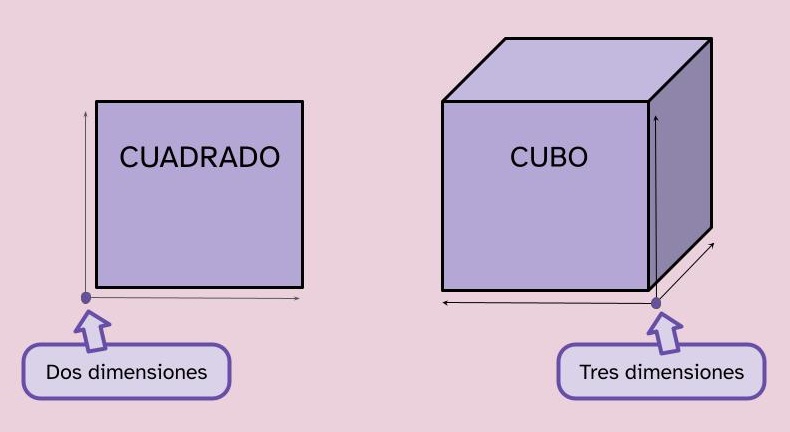
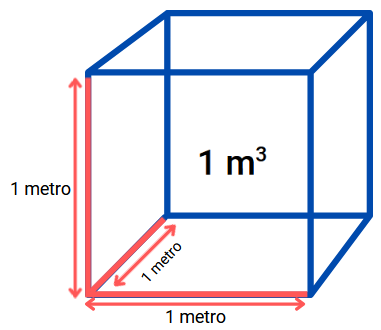
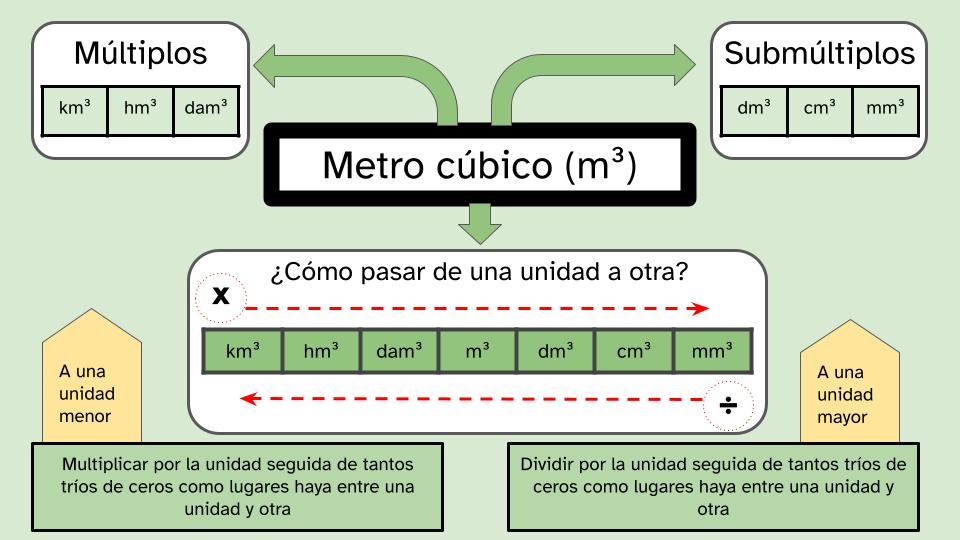
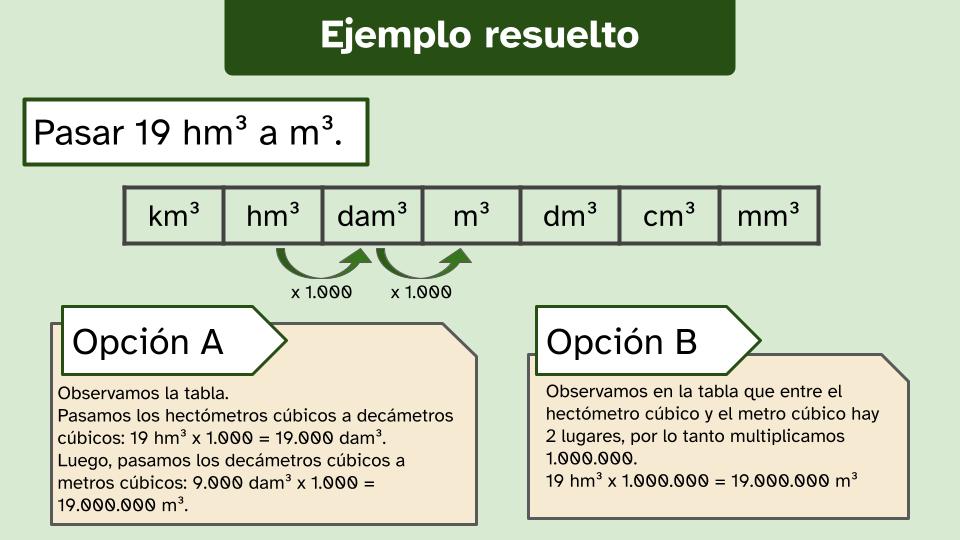
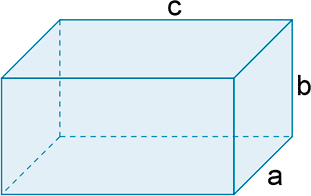
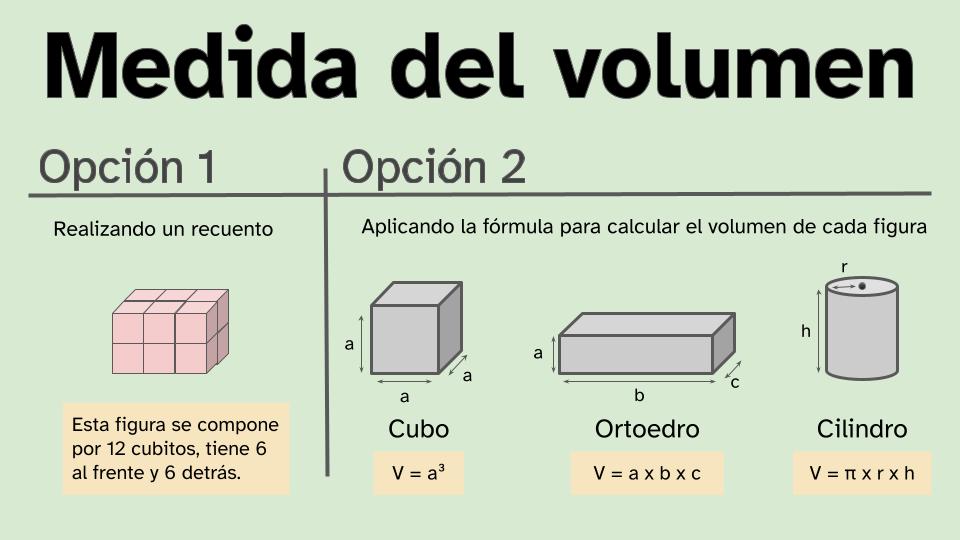
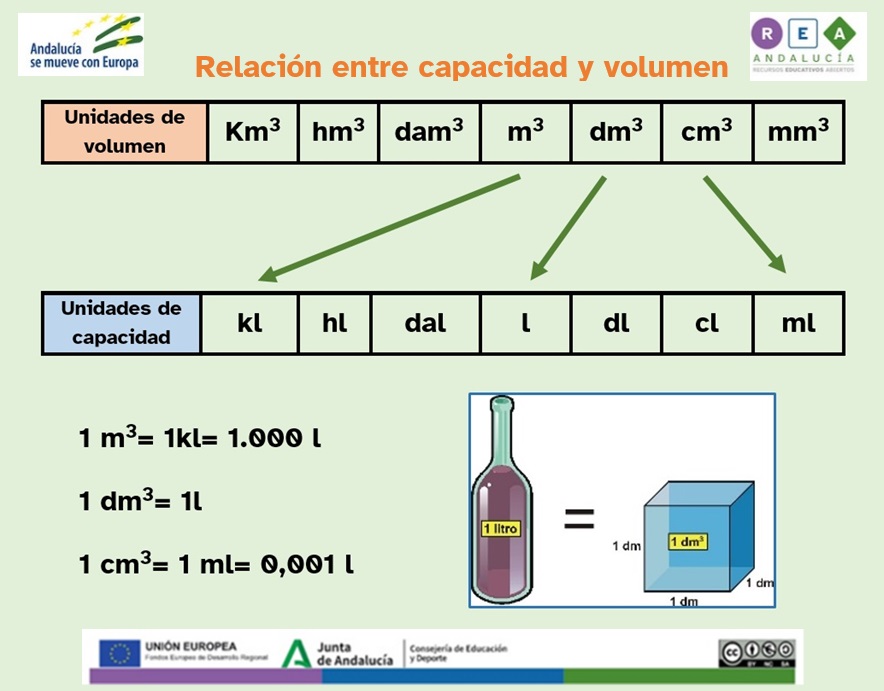
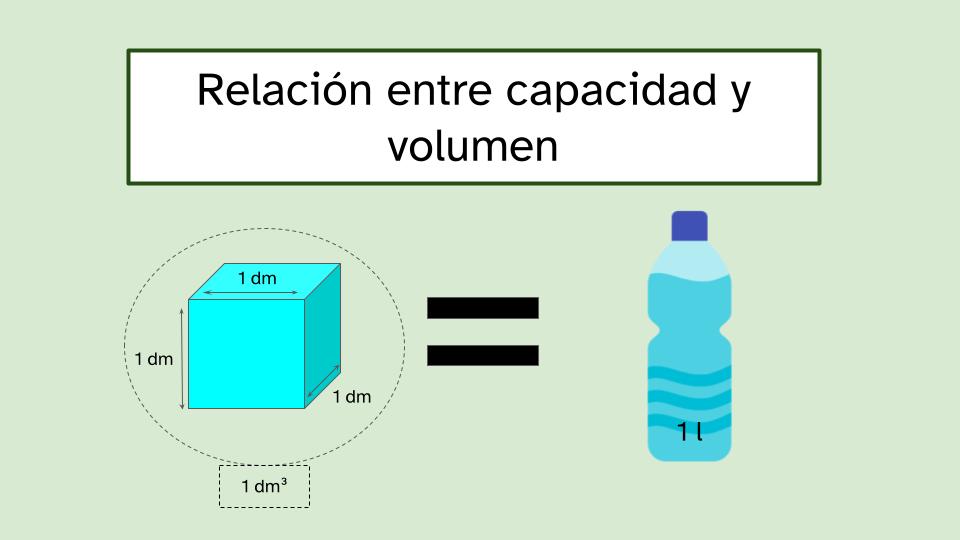
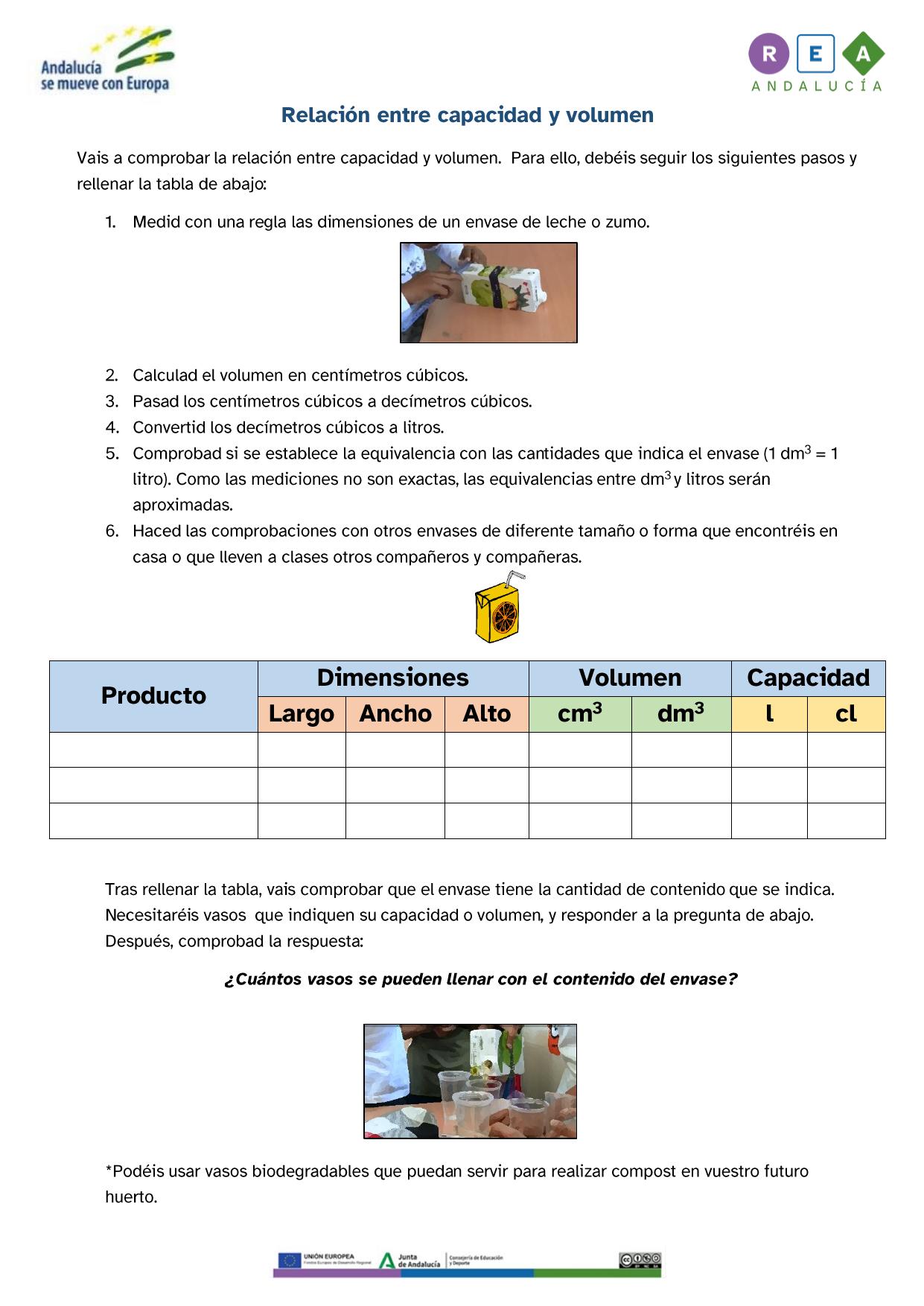
Descripción	REA para tercer ciclo de Educación Primaria sobre uso y cálculo de áreas y volúmenes
Persona de pedagogía terapéutica	Pilar Cuevas Castell
Persona elaboradora de contenido	Manuel Ángel Fernández Astorga
Persona elaboradora de contenido	Daniel González Luque
Persona elaboradora de contenido	Andrés Egea Martínez
Persona de soporte técnico	Alejandro Leal Cruz
Persona coordinadora del ciclo	Miguel Ángel González Lozano
Persona coordinadora de la materia	Juan Francisco Romero del Castillo
Organización	Dirección General de Formación del Profesorado e Innovación Educativa. Consejería de Educación y Deporte. Junta de Andalucía.
Licencia	Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0

Este contenido fue creado con eXeLearning, el editor libre y de fuente abierta diseñado para crear recursos educativos.

Logo Andalucía se mueve con Europa

Créditos de los recursos externos

Página 1

Imagen de la portada del REA 1 del tercer ciclo de primaria de matemáticas — Elaboración propia. *Portada para los REA del tercer ciclo de Matemáticas de Educación Primaria*(CC BY-NC-SA)

Página 2

dibujo de una brújula — Imagen procedente de *ARASAAC*. *Posición* (CC BY-NC-SA)

Ilustración de una balanza que está midiendo la masa una sandía. — Elaboración propia empleando iconos de icon-icons (1 y 2). *Magnitud masa* (CC BY-NC-SA)

Ilustración del planeta Tierra rodeado de distintas especies de seres vivos. — Elaboración propia empleando iconos de icon-icons (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 y 16). *Especies* (CC BY-NC-SA)

fotografía de un pequeño huerto escolar con diferentes plantas hortícolas y con un sistema de riego automático. Además, se distinguen una niña y un niño cuidando y observando las plantas del huerto. — Elaboración propia. *Huerto de autocultivo*(CC BY-NC-SA)

dibujo de un cubo de color rojo en perspectiva de tres dimensiones — Imagen procedente de *ARASAAC*. *Arista en cubo* (CC BY-NC-SA)

Ilustración de una regla bajo un lápiz. — Elaboración propia empleando iconos de icon-icons (1, 2). *Longitud* (CC BY-NC-SA)

ilustración de una hoja que contiene muchas etiquetas para recortar — Imagen procedente de *ARASAAC*. *Etiqueta* (CC BY-NC-SA)

Ilustración de dos dibujos proporcionales de una casa. El dibujo de la izquierda tiene el doble de tamaño que el de la derecha y así lo indican sus medidas. — Elaboración propia. *Proporción geométrica*(CC BY-NC-SA)

ilustración de un mapa en el que hay señalado un punto en concreto en él — Imagen procedente de *Icon-icons*. *Ubicación en plano* (CC BY-NC-SA)

Ilustración de cuatro figuras planas de diferentes colores, entre ellas un círculo y un pentágono. — Imagen procedente de *Carolina Albalat*. *Figuras planas* (CC BY-NC-SA)

pictograma en el que aparecen figuras de niñas y niños sentadas en el suelo y formando un círculo en el aula — Imagen procedente de *ARASAAC*. *Asamblea* (CC BY-NC-SA)

ilustración de una plano esquemático de un edificio y sobre él unas manos con un lápiz y una regla simulando su realización — Imagen procedente de *PxHere*. *Croquis* (CC BY-NC-SA)

infografía bajo el título magnitudes con iconos de: un termómetro, un peso, una regla y un reloj. — Elaboración propia empleando iconos de icon-icons (1, 2, 3 y 4). *Magnitudes* (CC BY-NC-SA)

ilustración de un detective con una gran lupa en la mano a través de la cual observa un signo de interrogación — Imagen procedente de *Wikimedia*. *Curioso* (CC BY-NC-SA)

Ilustración con dos figuras: un cuadrado en el que se señalan sus dos dimensiones y un cubo en el que se señalan sus tres dimensiones. — Elaboración propia. *Dimensión física* (CC BY-NC-SA)

Ilustración con el título: unidad de medida en gran tamaño y objetos medidos con diferentes magnitudes: una botella de agua de un litro, un tablón de un metro, un peso que mide en kilogramos y los segundos en un reloj — Elaboración propia empleando iconos de icon-icons (1, 2, 3 y 4). *Unidades de medida* (CC BY-NC-SA)

Imagen procedente de *PxHere*. *Plano* (CC BY-NC-SA)

Imagen de una balanza que se inclina hacia la izquierda. En el platillo de la derecha se ve un icono de error en color rojo y en el platillo de la izquierda se distinguen varios símbolos de correcto de fiferentes tamaños todos ellos en color verde. — Elaboración propia. *Balanza que indica aquello más apropiado o beneficioso*(CC BY-NC-SA)

Ilustración de una botella de agua junto a un vaso lleno. — Elaboración propia empleando icono Icon-icons. *Capacidad* (CC BY-NC-SA)

imagen de un huerto — Imagen procedente de *Freepik*. *Hortalizas en huerto* (CC BY-NC-SA)

ilustración de una maqueta de un edificio moderno sobre una mesa — Imagen procedente de *ARASAAC*. *Maqueta* (CC BY-NC-SA)

Página 3

fotografía de una cosechadora recogiendo el cereal en una producción agraria — Imagen procedente de *PxHere*. *Agrario* (CC BY-NC-SA)

Pictograma que representa algo importante. En el pictograma aparecen dos caras observando un objeto circular y de color rojo situado en medio y encima de las cara hay signos de admiración. — Imagen procedente de *ARASAAC*. *Importante* (CC BY-NC-SA)

imagen de una serie de un huerto en el que hay sembradas diferentes hortalizas bajo un cartel en el que resaltan las palabras 'Sembramos futuro'. En la zona central inferior está el personaje Retor con un bocadillo que contiene tres puntos suspensivos — Elaboración propia. *Sembramos futuro*(CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Hoja de ruta' — Elaboración propia. *Hoja de ruta*(CC BY-NC-SA)

Página 4

imagen de tres de instrumentos de medida como son: una balanza, una cinta métrica y un matraz bajo el título: '¿Recuerdas como...?' Además, toda la base de la imagen está decorada de pequeñas plantas que salen de la tierra. En la zona central inferior está el personaje Retor con un bocadillo que contiene tres puntos suspensivos — Elaboración propia. *Recuerdas cómo...*(CC BY-NC-SA)

la imagen es una tabla resumen de las unidades de medida. Se describen las siguientes magnitudes: longitud, masa y capacidad. Para la descripción se aclaran las siguientes cuestiones para cada una de ellas: ¿Para qué sirve? ¿Cuál es su unidad de medida principal? ¿Con qué instrumento se puede medir? En la segunda fila se describe la magnitud de la longitud. Se explica que la longitud es la distancia entre dos puntos y que la unidad de medida principal es el metro. Además, aclara que la cinta métrica o la regla son instrumentos para medir la longitud y, por último, se pone como ejemplo de la vida cotidiana la longitud de una persona. En la tercera fila se describe la magnitud de la masa. Se explica que la masa es la cantidad de materia que contiene un cuerpo u objeto y que la unidad de medida principal es el gramo. Además, aclara que la báscula o la balanza son instrumentos para medir la masa y, por último, se pone como ejemplo de la vida cotidiana la cantidad de harina necesaria para hacer pan. En la cuarta fila se describe la magnitud de la capacidad. Se explica que la capacidad es el volumen o el espacio que ocupa un cuerpo u objeto y que la unidad de medida principal es el litro. Además, aclara que la probeta o la jarra medidora son instrumentos para medir la capacidad y, por último, se pone como ejemplo de la vida cotidiana la cantidad de agua que cabe en una botella — Elaboración propia. *Tabla de unidades de medida*(CC BY-NC-SA)

la imagen es una tabla donde se relacionan las diferentes unidades de medida de cada una de las siguientes magnitudes: longitud, masa y volumen. Se acompañan, en cada caso, de elementos visuales como un flexómetro y una regla en el caso de logintud, dos tipos diferentes de máquinas para registrar el peso y una botella de plástico y una jarra con indicación de cantidad en el caso de la capacidad — Elaboración propia. *Tabla de conversión entre magnitudes*(CC BY-NC-SA)

Elaboración propia. Video: unidades de medida (CC BY-NC-SA)

Página 5

Retor se sitúa a la derecha del texto y lleva en las manos una regadera que echa agua sobre una planta — Elaboración propia. *Rétor riega una planta con números y porta utensilios hortícolas*(CC BY-NC-SA)

infografía en la que aparecen árboles y encima de éstos los 4 elementos básico que necesitan las platas para vivir: aire, agua, luz y tierra. Además, junto a cada uno de los elementos aparecen los personajes: Motus, Clavis, Kardia y Lumen — Elaboración propia. *¿Qué necesitan las plantas para vivir?*(CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Plantilla para la investigación' que se trata de una plantilla para hacer una investigación en color verde sobre las cuatro necesiadades básicas de las plantas. Para comenzar se debe elegir la necesidad básica que se va a investigar, es decir, aire, agua, tierra y luz. A continuación, aparecen recuadros a completar de las tres fases más importantes en una investigación: una hipótesis, un proceso y una conclusión — Elaboración propia. *Plantilla para la investigación*(CC BY-NC-SA)

Página 6

ilustración de un lápiz trazando una línea — Elaboración propia empleando icono de Icon-icons. *Trazar con un lápiz* (CC BY-NC-SA)

imagen de una hoja con cuadrícula — Elaboración propia empleando icono de Icon-icons. *Cuadrícula* (CC BY-NC-SA)

ilustración de dos figuras con las puntas redondeadas de diferentes tamaños pero proporcionales — Elaboración propia empleando icono de Icon-icons. *Proporcional* (CC BY-NC-SA)

fotografía de un folio blanco con trazos azules hechos con un pincel — Imagen procedente de *Pexels*. *Trazo* (CC BY-NC-SA)

imagen de una carpeta de color verde en cuya etiqueta se pueden leer las palabras 'Reconociendo el terreno' y que contiene un dibujo de un huerto, unos planos de un colegio y una carpeta con folios. En el lado izquierdo se puede apreciar a retor con una lupa en una mano y un flexómetro en otra — Elaboración propia. *Reconociendo el terreno* (CC BY-NC-SA)

bocadillo de cómic con puntos en su interior simulando que contiene palabras — Elaboración propia empleando icono de Icon-icons. *Bocadillos con palabras* (CC BY-NC-SA)

silueta de un autobús escolar — Elaboración propia. *Bus escolar* (CC BY-NC-SA)

ilustración de un ojo mirando desde arriba a un colegio — Elaboración propia empleando iconos de icon-icons (1 y 2). *Vista arriba* (CC BY-NC-SA)

Página 7

imagen con diferentes símbolos y figuras matemáticas relacionadas con la superficie y el volumen sobre un fondo verde claro — Elaboración propia. *Aprender medidas de superficie y capacidad* (CC BY-NC-SA)

imagen de una pizarra en color verde donde destacan las palabras 'Descubre y aprende' y donde se distinguen la imagen de un rectángulo y de un ortoedro, además de el símbolo de metro cuadrado y de metro cúbico — Elaboración propia. *Descubre y aprende* (CC BY-NC-SA)

Página 8

imagen perteneciente a la segunda página del documento PDF 'Cálculo de areas de figuras con volumen' — Elaboración propia. *Cálculo de áreas de figuras con volumen* (CC BY-NC-SA)

ilustración de un croquis de un huerto bajo el título 'la superficie'. En el croquis están señaladas sus dimensiones (23 me de ancho y 10 metros de largo). A la izquierda del croquis se explica que el huerto tiene una extensión de 230 metros cuadrados. Y que por lo tanto, su superficie es de 230 m². Además, se aclara mediante un bocadillo que un metro cuadrado se expresa así: 1m2 — Elaboración propia. *Apoyo visual: superficie* (CC BY-NC-SA)

ilustración de una figura que mide 3 metros cuadrados y del cálculo de su área dividiéndola en 3 cuadrados de 1 metro cuadrado cada uno — Elaboración propia. *Concepto de metro cuadrado* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Cálculos de áreas de figuras planas' — Elaboración propia. *Cálculo de área de figuras planas* (CC BY-NC-SA)

imagen de Retor con un casco de obra, un lápiz entre su cabeza y la cara, unas gafas de protección ocular y un flexómetro en su mano izquierda — Elaboración propia. *Rétor con flexómetro mide distancias* (CC BY-NC-SA)

Elaboración propia. Averiguar el área de figuras como el cuadrado, el rectángulo, el romboide, triángulo, el rombo y el trapecio (CC BY-NC-SA)

Elaboración propia. Cómo hallar el área de un círculo (CC BY-NC-SA)

Elaboración propia. Cómo calcular el área de un polígono regular (CC BY-NC-SA)

Elaboración propia. Cálculo del área de la superficie de figuras con volumen como el cono, la esfera y el cilindro (CC BY-NC-SA)

Página 9

imagen donde se pueden observar 3 superficies en forma de cuadrado, que representan un milímetro cuadrado, un centímetro cuadrado que es 100 veces mayor que el milímetro cuadrado y un decímetro cuadrado que es 100 veces mayor que el centímetro cuadrado. También podemos observar en la parte superior de la imagen todas las unidades de medida de superficie y la misma relación y proporción de tamaño en la que la primera es 100 veces mas pequeña que la siguiente y así se mantiene esta prporción sucesivamente con las demás — Elaboración propia. *Relación de tamaño entre el decímetro cuadrado* (CC BY-NC-SA)

imagen de Retor con un casco de obra, un lápiz entre su cabeza y la cara, unas gafas de protección ocular y un flexómetro en su mano izquierda. Está rodeado de múltiplos del metro cuadrado como son el decámetro, hectómetro, kilómetro y miriámetro — Elaboración propia. *Rétor y medidas y múltiplos de superficie* (CC BY-NC-SA)

esquema de los múltiplos y submúltiplos del metro cuadrado y explicación de como pasar de unas unidades a otras. En cuanto a los múltiplos, el esquema habla de 3: el kilómetro cuadrado, el hectometro cuadrado y el decámetro cuadrado. En relación a los submúltiplos, la infografía indica que son tres: el decímetro cuadrado, el centímetro cuadrado y el milímetro cuadrado. Finalmente, se habla que para pasar de unas unidades a otras, habrá que multiplicar si se pasa de una unidad mayor a otra menor y por el contrario, habrá que dividir si se pasa de una unidad menor a otra mayor. Además, se aclara que se multiplicará o dividirá por la unidad seguida de tantos pares de ceros como de lugares hay entre las unidades — Elaboración propia. *Apoyo visual: múltiplos y submúltiplos de unidades de superficie* (CC BY-NC-SA)

se puede ver una tabla en la que se diferencian las distintas unidades de medida de superficie ordenadas de menor a mayor y encuadradas, en dicha tabla se coloca las cifras 8 y 9 en los metros cuadrados y la cifra 7 en decámetros cuadrados, la coma que delimita la parte entera de un número se encuentra encuadrada en los metros cuadrados. Alrededor del número a parecen unas notas que explican el proceso seguido en la colocación de las cifras y comas en dicho cuadrante, a lo que se añade unas flechas que indican el movimiento a seguir por la coma para pasar de metros cuadrados a hectómetros cuadrados, y la necesidad de añadir los ceros correspondientes para obtener la solución — Elaboración propia. *Paso 3 de cambio de unidades* (CC BY-NC-SA)

infografía con los múltiplos y submúltiplos del metro cuadrado ordenados de mayor a menor comenzando por la izquierda y que además muestra la operación necesaria para pasar de una unidad a otra y la cantidad de unidades que contiene con respecto a la siguiente — Elaboración propia. *Tabla de cambio de unidades* (CC BY-NC-SA)

se puede ver una tabla en la que se diferencian las distintas unidades de medida de superficie ordenadas de menor a mayor y encuadradas — Elaboración propia. *Paso 1 de cambio de unidades* (CC BY-NC-SA)

ilustración bajo el títlo la hectárea de un cuadrado de 100 metros de lado y en la que además aparecen dos recordatorios: 1 hectárea es igual a 1ha y una hectárea es 10.000 metros cuadrados — Elaboración propia. *La hectárea* (CC BY-NC-SA)

en la imagen se visualiza un huerto en el cual se sitúan unos carteles informativos con algunos consejos a tener en cuenta para buscar el lugar más adecuado para situar o acomodar un nuevo huerto. Se obserba un árbol que simboliza la necesidad de disponer de la opción de tener algo de sombra; un grifo que representa la importancia de tener agua cerca del huerto; una valla alrededor del huerto para aconsejar una mayor protección, un camión que representa la necesidad del acceso de vehículos, el Sol representa la necesidad muy frecuente de el mismo para el huerto, la abundante tierra alrededor representa la necesidad de disponer de una gran cantidad de tierra y hueco en el huerto para tener una buena profundidad y calidad del mismo — Elaboración propia. *Construir un huerto* (CC BY-NC-SA)

Elaboración propia. Relación de tamaño entre el decímetro cuadrado, el centímetro cuadrado y el milímetro cuadrado (CC BY-NC-SA)

Elaboración propia. Cambios de unidades (superficie) (CC BY-NC-SA)

Página 10

pictograma con tres recipientes distintos: una bolsa, una botella y una fiambrera — Imagen procedente de *ARASAAC*. *Recipiente* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF '¿Qué es el volumen?' — Elaboración propia. *Captura de pantalla de página 2 del documento '¿Qué es el volumen?'* (CC BY-NC-SA)

imagen que muestra tres figuras sobre un plano de color azul. Una figura amarilla y otra azul de igual forma: como un dado alargado y más bajo que ancho (ortoedros), Una tercera figura de color rojo que tiene forma de dado. (un cubo) — Elaboración propia. *Disposición 1 de figuras con volumen en el plano* (CC BY-NC-SA)

tiene forma de dado (cubo) transparente con los bordes de color azul excepto el borde lateral, el borde de la base y el borde del fondo de la parte izquierda que están coloreados de rojo. Cada uno de estos bordes tienen rotulada la palabra 1 metro (indicado con una flecha roja) y dentro del cubo el rótulo un metro cúbico escrito con el número 1, una eme y un tres sobre la eme que indica que se lee 'cúbico' — Elaboración propia. *Disposición 3 de figura con volumen en el plano* (CC BY-NC-SA)

imagen donde se ve una pequeña piscina de superficie en el patio trasero de hierba de una finca, dentro de la cual hay 3 personas jóvenes tomando un baño — Elaboración propia. *Piscina en jardín de hierba cerca de la playa* (CC BY-NC-SA)

imagen que muestra dos figuras a modo de dado alargado. Las figuras son iguales, de color rojo pero colocadas de forma diferente sobre un plano azul que hacen pensar que son figuras diferentes — Elaboración propia. *Disposición 2 de figuras con volumen en el plano* (CC BY-NC-SA)

imagen de una caja de cartón que mide un metro de alto, un metro de ancho y un metro de largo. En la imagen hay un texto que dice: Esta caja ocupa un espacio de un metro cúbico, es su volumen. También aparece una nota que recuerda que un metro cúbico es igual a 1m3. Todo lo descrito aparece bajo el título: 'El volumnen' — Elaboración propia. *Apoyo visual: volumen* (CC BY-NC-SA)

imagen de Retor que sostiene un cubo en la mano — Elaboración propia. *Retor sostiene un cubo en la mano* (CC BY-NC-SA)

Página 11

imagen de Retor que sostiene un cubo de Rubik en la mano — Elaboración propia. *Retor que sostiene un cubo de Rubik en la mano* (CC BY-NC-SA)

la infografía tiene el título 'Unidades de Volumen', y dos subtítulos. Subtítulo 1: 'Múltiplos y submúltiplos del metro cúbico'. Debajo aparece una tabla en la que se indica la unidad, el símbolo y la equivalencia con los metros cúbicos de cada unidad. Múltiplos: Kilómetro cúbico =1.000.000.000 metros cúbicos. Hectómetro cúbico = 1.000.000 metros cúbicos. Decámetro cúbico = 1.000 metros cúbicos. Unidad principal: Metro cúbico = 1 metro cúbico. Submúltiplos: Decímetro cúbico = 0,001 metros cúbicos. Centímetro cúbico = 0,000001 metros cúbicos. Milímetro cúbico = 0,000000001 metros cúbicos. Subtítulo 2: 'Conversión de unidades de volumen'. Debajo aparece una ilustración en la ser ven las unidades en forma de escalera. A la derecha se indica con flechas amarillas que para pasar de una unidad superior a otra inferior se multiplica por mil. A la izquierda se indica con flechas rojas que para pasar de una unidad inferior a otra superior se divide entre mil — Elaboración propia. *Unidades de volumen: múltiplos, submúltiplos y conversión* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Problemas con el agua' — Elaboración propia. *Captura de pantalla de la página 2 del documento 'Problemas con el agua'* (CC BY-NC-SA)

imagen donde se observa un camión con un cajón amarillo — Elaboración propia. *Camión de obra* (CC BY-NC-SA)

imagen de un esquema de los múltiplos y submúltiplos del metro cúbico y explicación de como pasar de unas unidades a otras. En cuanto a los múltiplos, el esquema habla de 3: el kilómetro cúbico, el hectometro cúbico y el decámetro cúbico. En relación a los submúltiplos, la infografía indica que son tres: el decímetro cúbico, el centímetro cúbico y el milímetro cúbico. Finalmente, se habla que para pasar de unas unidades a otras, habrá que multiplicar si se pasa de una unidad mayor a otra menor y por el contrario, habrá que dividir si se pasa de una unidad menor a otra mayor. Además, se aclara que se multiplicará o dividirá por la unidad seguida de tantos tríos de ceros como de lugares hay entre las unidades — Elaboración propia. *Apoyo visual: múltiplos y submúltiplos* (CC BY-NC-SA)

imagen de una infografía sobre cómo resolver un ejerciccio de pasar 19 hm3 a m3. En primer lugar se muestra una tabla con los múltiplos y submúltiplos del metro cúbico. En dicha tabla aparecen dos flechas, una que va desde hm3 al dam3 y otra que va desde dam3 al m3. Bajo cada una de las flechas se aprecia la expresión: por mil.Luego se ofrecen las dos opciones para resilver el ejercicio. La opción A, dice que multipliquemos 19 por 1.000 para pasar de hm3 a dam3 y lugo lo volvamos a multiplicar por 1.000 para pasar la cantidad de dam3 a m3. La opción B, muestra la posibilidad de multiplicar 19hm3 por 1.000.000 para pasarlos a metros directamente, aclarando que se multiplica por 1.000.000 porque hay dos lugares entre los hm3 a los m3 — Elaboración propia. *Apoyo visual: ejemplo* (CC BY-NC-SA)

Página 12

imagen de un ortoedro (como un cubo más largo que alto) donde se ha rotulado la base y se han nombrado con las letras a, b y c una arista lateral, una superior y una oblícua respectivamente — Elaboración propia. *Medida del volumen 3* (CC BY-NC-SA)

imagen de un cubo de color violeta donde están rotuladas las partes del mismo: arista, vértice (con un punto rojo) y cara — Elaboración propia. *Medida del volumen 2* (CC BY-NC-SA)

fotografía de un edificio con forma de cilindro — Elaboración propia. *Medida del volumen 7* (CC BY-NC-SA)

ilustración del planeta Tierra redeada de multitud de cajas de cartón de diferentes tamaños — Elaboración propia. *Medida del volumen 6* (CC BY-NC-SA)

imagen de una figura compuesta por dos cilindros -uno amarillo y otro rosa- y un cubo rojo seguidos que se apoyan sobre un ortoedro de color verde en un plano azul — Elaboración propia. *Medida del volumen 5* (CC BY-NC-SA)

imagen de un cilindro violeta, una figura parecida a un rotulador sin punta y mucho más ancho. En esta figura se ha puesto la palaba arista a los lados curvos de la misma — Elaboración propia. *Medida del volumen 4* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Calcula el volumen' — Elaboración propia. *Calcula el volumen* (CC BY-NC-SA)

ilustración con una imagen de los tres cuerpos estudiados: cubo, ortoedro y cilindro. Bajo cada una de las imagénes se aprecian las fórmulas para calcular el volumen y sobre ellas el nombre — Elaboración propia. *Cálculo del volumen de diferentes figuras geométricas* (CC BY-NC-SA)

ilustración compuesta por dos partes: la parte de la izquierda trata una opción para medir el volumen de una figura. En concreto habla del recuento de cubitos para medir el volumen. Muestra una figura compuesta por 12 cubos, 6 al frente y 6 detrás y en dos alturas. La parte de la derecha trata sobre la opción para medir el volumen aplicando las fórmulas de las distintas figuras. Muestra la fórmula para medir el volumen de un cubo bajo uma imagen del mismo; la fórmula para el cálculo de un ortoedro bajo una imagen del mismo; y finalmente la fórmula para calcular el volumen de un ciclindro bajo una imagen del mismo. Fórmula del cubo: 'V = a3'.Fórmula del ortoedro: 'V = a x b x c'.Fórmula del cilindro: 'V = π x r x h' — Elaboración propia. *Apoyo visual: cálculo del volumen* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'La medida del volumen' — Elaboración propia. *Medida del volumen 1* (CC BY-NC-SA)

ilustración de un brick de leche — Elaboración propia. *Medida del volumen 8* (CC BY-NC-SA)

imagen de una figura compuesta de 24 dados rojos dispuestos en dos filas de 12 dados cada una una. Los doce dados de la fila superiror tienen rotulado su número, del 1 al 12 — Elaboración propia. *Medida del volumen con 12 cuadraditos* (CC BY-NC-SA)

Página 13

el título de la imagen es 'Relación entre capacidad y volumen'. Aparece una tabla horizontal con las unidades de volumen y otra debajo con las unidades de capacidad. Hay tres flechas que unen tres equivalencias. Son: UN m3= 1kl= 1.000 l. Un dm3= 1l. Un cm3= 1 ml= 0,001 l. A la derecha aperece una botella llena de líquido que indica que contiene 1 litro con el signo igual a un cubo que tiene un volumen de un decímetro cúbico — Elaboración propia. *Relación entre masa y volumen* (CC BY-NC-SA)

imagen en la que se comprueba que un cubo de un 1 dm3 tiene la misma capacidad que 1 litro de agua. De forma que apararece un signo de igual entre el cubo de 1 dm3 y una botella de agua de un litro — Elaboración propia. *Apoyo visual: relación entre masa y volumen* (CC BY-NC-SA)

imagen en la cual aparecen tres objetos: a la izquierda un cubo de basura de color verde. En el centro un dado de color blanco con las caras de 1, 3 y 5. A la derecha un tetra-brik de leche de color gris — Elaboración propia. *Actividad sobre capacidad* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Relación entre volumen y capacidad' — Elaboración propia. *Actividad sobre volumen y capacidad* (CC BY-NC-SA)

imagen perteneciente a la segunda página del documento PDF 'Retos huertomáticos' — Elaboración propia. *Huertomáticos* (CC BY-NC-SA)

Página 14

imagen de la maqueta del huerto finalizada siguiendo las indicaciones del boceto. Se observa que está situado entre dos paredes blancas. La de la izquierda con una ventana y la de la derecha con 2 ventanas. El suelo es blanco también. En el suelo, a la izquierda hay un cajón de huerto con forma cuadrada realizado con un envase, y a la derecha, más arriba, un cajón de huerto con forma rectangular realizado con el lateral de otro envase. Ambos cajones están pintados de marrón, están llenos de tierra y tienen unos cables que simular las mangueras del riego por goteo. A su derecha hay un grifo conectado con un depósito de agua realizado con un bote de especias — Elaboración propia. *Maqueta huertos* (CC BY-NC-SA)

imagen donde se aprecia una tabla con las siguientes indicaciones: el cajón de huerto 1 tiene una superficie de 1,44 metros cuadrados. Un volumen de 0,432 metros cúbicos. Se necesitan 432 litros de tierra. El Cajón de huerto 2 tiene una superficie de 3 m2. Un volumen de 0,9 metros cúbicos. Se necesitan 900 litros de tierra. El Bidón tiene un volumen de 1 metro cúbico y puede almacenar 1.000 litros de agua — Elaboración propia. *Diseño de huerto* (CC BY-NC-SA)

imagen de una mesa de color marrón en la que hay un diseño de un huerto. Junto a la mesa hay un taburete y encima destacan las palabras 'Diseños que dan vida', también se puede ver sobre la mesa una escuadra. Retor aparece en el lado derecho inferior de la imagen con un lápiz sobre uno de los lados de su cara — Elaboración propia. *Diseños que dan vida* (CC BY-NC-SA)

ilustración en la que aparece una silueta humana realizando una presentación de un huerto a un grupo de personas empleando una pizarra — Elaboración propia. *Exposición oral* (CC BY-NC-SA)

fotografía de un grupo de personas trabajando conjuntamente y que juntan sus puños como símbolo de cooperación — Imagen procedente de *PxHere*. *Trabajo colaborativo* (CC BY-NC-SA)

imagen de un esquema que recoge las cuatro fases o pasos para realizar el diseño de un huerto.Cada una de las fases se describe en un recuadro. La primera fase, titulada 'el boceto' anima a realizar un boceto con las principales características que va a tener el huerto que quieres diseñas y se acompaña de la imagen de un boceto. La segunda fase, titulada 'la maqueta' explica que se debe trasladar el boceto a una maqueta y para ello se ofrecen las siguientes recomendaciones: usar materiales reciclados, dar color a la maqueta, usar un fondo similar al real y decorarla. Se acompaña el texto con la forografía de una maqueta de un huerto. La tercera fase, titulada 'datos numéricos' habla de la necesidad de reflejar los datos de la superficie y el volumen de los elementos de un huerto, también se acompaña de la imagen de una tabla para recoger datos numéricos sobre volumen y superficie. Finalmente, la última fase, titulada 'ampliación' ofrece la posibilidad de realizar una maqueta empleando una impresora 3D y se acompaña de la imagen de una imoresora 3d — Elaboración propia. *Apoyo visual: pasos del diseño* (CC BY-NC-SA)

imagen de un boceto a lápiz en papel blanco con los elementos del huerto escolar. Se observa que está situado entre dos paredes. La de la izquierda con una ventana y la de la derecha con 2 ventanas. En el suelo, a la izquierda hay un cajón de huerto con forma cuadrada de 1,2 m de lado, y a la derecha, más arriba, un cajón de huerto con forma rectangular de 1 metro de ancho y 3 metros de largo. A su derecha hay un grifo y un depósito de agua de 1 metro cúbico. Los cajones de huerto indican que tienen 0,3 metros de altura en la realidad — Elaboración propia. *Boceto* (CC BY-NC-SA)

imagen donde se aprecia el ejemplo de una impresora 3d imprimiendo una ficha de ajedrez — Imagen procedente de *Pixabay*. *Impresora 3D* (CC BY-NC-SA)

imagen de retor con un bocadillo de texto que pretende hacer referencia al texto que se muestra a la derecha de ésta — Elaboración propia. *Rétor dice...* (CC BY-NC-SA)

Página 15

imagen de una tabla que contiene una rúbrica. La primera fila en amarillo corresponde a los diferentes niveles de consecución y la primera columna en naranja corresponde a los diferentes contenidos trabajados — Elaboración propia. *Rúbrica de autoevaluación* (CC BY-NC-SA)

imagen de una diana de cuatro discos y dividida en 4 partes iguales en forma de cuña. El disco más pequeño y central es de color rojo y tiene el marcador 1; el siguiente de color azul y con el marcador 2; el tercero de color negro con el marcador 3; y el disco más externo de color blanco y con el marcador 4 — Imagen procedente de *Rosalía Esther Reyes Lechuga*. *Diana de autoevaluación* (CC BY-NC-SA)

imagen de una rúbrica formada por una tabla de 5 columnas y 4 filas. La primera columna de color naranja contiene 3 de los contenidos a evaluar: trabajo individual, trabajo en equipo y ayuda o atención al resto del equipo; la primera fila en color amarillo contiene los diferentes niveles de adquisición de los contenidos: iniciado, suficiente, bueno y excelente. El resto de celdas aparecen en color blanco y contienen la descripción del nivel de adquisición de los diferentes contenidos — Elaboración propia. *Rúbrica de autoevaluación* (CC BY-NC-SA)

imagen de un camino en el que se distinguen pasos recorriéndolo. Al final del camino se encuentra la meta marcada con la palabra fin y con globos de distintos colores rodeándola. Todo se encuentra sobre un fondo verde con pequeñas plantas y en el que resaltan las palabras 'Explica cómo lo lograste'. Retor aparece en la zona inferior, en el centro, con unas gafas de color negro — Elaboración propia. *Rétor: explica cómo lo lograste* (CC BY-NC-SA)

imagen que muestra un resumen con el fondo de un huerto donde predomina el color verde. En la parte superior aparece el título 'diseña para una buena cosecha' enmarcado en un retángulo con fondo mostaza. En su parte izquierda a parece el personaje retor sobre un huerto. Bajo el título hay dos carteles: uno a la derecha con fondo celeste con el texto: cáclulo de volúmenes: ortoedro, cubo y cilindro. Relación entre el volumen y la capacidad y otro a la izquierda con el texto en fodo amarillo: concepto de superficie.Unidad principal de superficie: múltiplos y submúltiplos del metro cuadrado. Medidas agrarias de superficie: la hectárea. Bajo estos cuadros tenemos uno a la izquierda con fondo rosa y con el texto: Concepto de volumen. Unidad principal de volumen Múltiplos y submúltiplos del metro cúbico. Uso del metro cúbico en la vida real. A su derecha hay otro cuadro con fondo blanco en el que podemos leer: ahorro de agua y optimizar los rcursos natuales; dentro de este cuadro, a la derecha hay una imagen de un grifo con dos gotas de agua saliendo de él — Elaboración propia. *Resumen: diseña para una buena cosecha* (CC BY-NC-SA)

Página 16

Algunos símbolos pictográficos utilizados son propiedad del Gobierno de Aragón y han sido creados por Sergio Palao para ARASAAC (http://www.arasaac.org) , que los distribuye bajo Licencia Creative Commons BY-NC-SA

Página 17

Las fichas ofrecidas al alumnado a lo largo del REA han sido realizadas por todas las personas elaboradoras de contenidos de la presente obra y tienen licencia CC BY-SA.

Página 18

Los documentos PDF de transcripción de texto de los subtítulos de los vídeos así como los propios subtítulos de dichos vídeos ofrecidos al alumnado a lo largo del REA han sido realizadas por todas las personas elaboradoras de contenidos de la presente obra y tienen licencia CC BY-SA.

Página 19

Los documentos de apoyo auditivo ofrecidos al alumnado a lo largo del REA han sido realizadas por todas las personas elaboradoras de contenidos de la presente obra y tienen licencia CC BY-SA.

Historial de versiones

Elaborado por:	Servicio de Innovación Educativa de la Consejería de Educación de la Junta de Andalucía.
Versión:	01	Fecha de publicación:	10 de julio de 2022	Primera versión

Aquí tienes el archivo fuente para editar este REA

Icono proyecto REA Andalucía en el que puede verse representados los tres colores del Diseño Universal para el Aprendizaje

Este REA se ha publicado bajo Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0

Esto significa que tienes la posibilidad de poder usarlo, descargarlo, redistribuirlo y modificarlo para adaptarlo a tus necesidades.

Sigue estos pasos para usar/redistribuir/modificar este REA:

1. Descarga el archivo fuente. Con esto tienes el recurso original en formato editable.

2. Modifícalo usando eXeLearning.

3. Si aun no lo tienes, descarga e instala el estilo EducaAnd.

4. Si lo modificas, has de reconocer la autoría y publicarlo con la misma licencia (CC BY-SA-NC).

Puedes usar esta cita para referenciarlo:

Este REA es una adaptación del recurso original "Diseña para una buena cosecha" del Proyecto REA Andalucía de la Consejería de Educación y Deporte de la Junta de Andalucía, que lo distribuye bajo licencia de CC BY-SA-NC.

Descargar el fichero .elp