Diccionario
Abalorios
Remunerar




Hay multitud de situaciones en las que la relación entre dos magnitudes se puede expresar a través de una función lineal, aquí vamos a ver cómo se puede expresar esta relación y las ventajas que se pueden obtener.
Dependencia funcional mediante tablas
 Una forma de recaudar dinero es elaborar figuras artesanalmente que luego se pueden vender en un mercadillo. Un grupo de alumnos decide ponerse manos a la obra y crear abalorios con esta finalidad. Irene va a hacer collares que venderá a 2 euros la unidad y quiere realizar una estimación de de lo que va a ingresar, para ello crea una tabla que relaciona el número de collares que fabrica con los ingresos que tiene.
Una forma de recaudar dinero es elaborar figuras artesanalmente que luego se pueden vender en un mercadillo. Un grupo de alumnos decide ponerse manos a la obra y crear abalorios con esta finalidad. Irene va a hacer collares que venderá a 2 euros la unidad y quiere realizar una estimación de de lo que va a ingresar, para ello crea una tabla que relaciona el número de collares que fabrica con los ingresos que tiene.
| Collares | 1 | 4 | 8 | 12 | 15 | 20 |
| Ingresos (€) | 2 | 8 | 16 | 24 | 30 | 40 |
Como se puede observar hay una relación entre las dos magnitudes de modo que si se conoce una de ellas se puede conocer el valor de la otra, así si Irene ingresa 30€ es porque ha vendido 15 collares y si vende 25 collares ingresará 50€. Hay una dependencia funcional entre los collares y los ingresos. Esta dependencia se puede expresar en formato de tabla.
Juan decide fabricar anillos de latón, al igual que Irene crea una tabla para conocer sus ingresos.
| Anillos | 2 | 6 | 10 | 15 | 25 | 40 |
| Ingresos (€) | 3 | 9 | 15 | 22,5 | 37,5 | 60 |
A partir de la tabla se puede determinar que hay una relación directa entre los anillos fabricados y los ingresos obtenidos, se tiene una dependencia funcional entre ambas magnitudes.
Creación de la expresión analítica a partir de una tabla de valores
Tomando como referencia las tablas anteriores cabe preguntarse si se puede encontrar una expresión que permite relacionar las dos magnitudes.
| Collares | 1 | 4 | 8 | 12 | 15 | 20 |
| Ingresos (€) | 2 | 8 | 16 | 24 | 30 | 40 |
Como con la venta de cada collar se ingresan 2€, si llamamos \(x\) al número de collares que se venden e \(y\) a los ingresos que Irene obtiene se puede observar que \(y=2x\), esta expresión permite relacionar las dos magnitudes (variables).
De este modo se pueden conocer los ingresos para cualquier cantidad que se venda y saber lo que se ha vendido si se conocen los ingresos.
Si Irene vende 35 collares, los ingresos serán \(y=2\cdot 35=70\), análogamente si no ha ido controlando los collares que ha vendido pero al final de la jornada tiene 98€, entonces \(98=2\cdot x \rightarrow x=\dfrac{98}{2}=49\), luego ha vendido 49 collares.
Si nos fijamos en la tabla con los datos de la venta de anillos de Juan.
| Anillos | 2 | 6 | 10 | 15 | 25 | 40 |
| Ingresos (€) | 3 | 9 | 15 | 22,5 | 37,5 | 60 |
Si se venden dos anillos por 3€, cada anillo costará 1,5€, podemos observar que esta misma relación se mantiene con el resto de valores de la tabla. Llamando \(x\) al número de anillos e \(y\) a los ingresos, se tiene que \(y=1,5x\), al igual que anteriormente se pueden inferir ingresos a partir del número de anillos y se puede conocer el número de anillos que se han vendido si se cuenta con los ingresos.
Las expresiones analíticas permiten expresar de forma sencilla la relación existente entre dos variables.
Función de proporcionalidad
Las funciones obtenidas anteriormente a partir de tablas muestran una proporcionalidad entre las dos variables, a esta función se le llama función de proporcionalidad y su expresión analítica es \(y=mx\) donde m es la constante de proporcionalidad, también se puede expresar de la forma \( f(x)=mx\).
A \(m\) se le llama pendiente de la función y puede tomar valores positivos en el caso en que la proporcionalidad sea directa o negativos si es inversa.
Función lineal
La madre de Irene propone otra forma de colaborar, ella posee un comercio de electrónica, cada vez que realice una venta con valor superior a 50€ aportará 1€ que guardará en una hucha, cuesta 50 céntimos y que se compra con la primera aportación.
Tras la primera venta habrá en la hucha 50 céntimos pues los otros 50 se han dedicado a la compra de la hucha, tras 2 ventas habrá 1,5€, después de 3 ventas 2,5€ y así se puede ir llenando la hucha. ¿Habrá una expresión que relaciona el número de ventas con valor superior a 50€ con la recaudación para colaborar?
Se puede esperar que en la hucha habrá un euro por cada venta a lo que hay que restar 50 céntimos que se han dedicado a la compra de la hucha. Esto se puede expresar de la forma \(y=x-0,5\), siendo \(y\) la recaudación (en euros) y \(x\) el número de ventas. Esta sería la expresión que relaciona la aportación de la tienda en función de sus ventas.
A una expresión de la forma \(y=mx+n\) se la conoce como función lineal. Al igual que en el caso de la función de proporcionalidad \(m\) es la pendiente y \(n\) se conoce como ordenada en el origen.
La función de proporcionalidad es un caso particular de función lineal en el que la ordenada en el origen (\(n\)) es nula.

Objetos de adornos.
EjemploMe encantan estos abalorios para nuestras pulseras.
Las ecuaciones de la recta son distintas formas de expresar la relación que hay entre las variables dependiente e independiente
Las expresiones que hemos visto anteriormente muestran la función lineal dada en forma explícita, la variable dependiente (y) está despejada en un miembro \(y=mx+n\)
De esta forma se obtiene el valor de la variable dependiente de forma inmediata a partir de cualquier valor de la variable independiente.
Ecuación explícita conocidos un punto y la pendiente
Si se conoce un punto de la función y su pendiente se puede hallar la ecuación explícita.
Ejemplo:
Determina la la ecuación explícita de la recta que pasa por \((1,2)\) y tiene pendiente \(m=-1\).
La forma de la ecuación explícita es \(y=mx+n\), como \(m=-1\) entonces \(y=-x+n\), al pasar por el punto \((1,2)\) cuando \(x=1 \; y=2\). Sustituimos en la ecuación \(2=-1+n \rightarrow 3=n\) luego la ecuación explícita es \(y=-x+3\).
Ecuación explícita conocidos dos puntos
Ejemplo:
Halla la ecuación explícita de la recta que pasa por los puntos \(A(1,2)\) y \(B(0,3)\)
Como la recta pasa por los dos puntos, estos tienen que verificar la ecuación \(y=mx+n\), sustituyendo se tiene:
\( \left\{ \begin{array}{l} 2=m \cdot 1 +n \\ 3=m \cdot 0 +n \end{array} \right. \) si nos fijamos en la segunda ecuación se tiene que \( n=3\), sustituyendo en la primera ecuación \(2=m+3 \rightarrow m=2-3=-1\). Luego la ecuación explícita de la recta que pasa por \(A\) y \(B\) es \(y=-x+3\).
Si se conoce un punto \(P(x_0,y_0)\) y la pendiente \(m\), la función se puede expresar como \(y-y_0=m(x-x_0)\).
Ejemplo: Halla la ecuación punto-pendiente de la recta que pasa por\( P(1,2)\) y tiene pendiente \(m=3\), entonces basta con sustituir en la fórmula anterior para obtener la ecuación solicitada \(y-2=3(x-1)\).
Si tenemos la ecuación punto-pendiente se puede pasar a la explícita despejando la variable dependiente \(y\), en el ejemplo anterior \(y-2=3(x-1) \rightarrow y=3x-3+2 \rightarrow y=3x-1\).
En ese caso todos los elementos se pasan a un miembro quedando igualado a 0, su expresión queda \(ax+by+c=0\)
Paso de ecuación explícita a implícitaPaso de ecuación implícita a explícita
 Función de proporcionalidad
Función de proporcionalidad
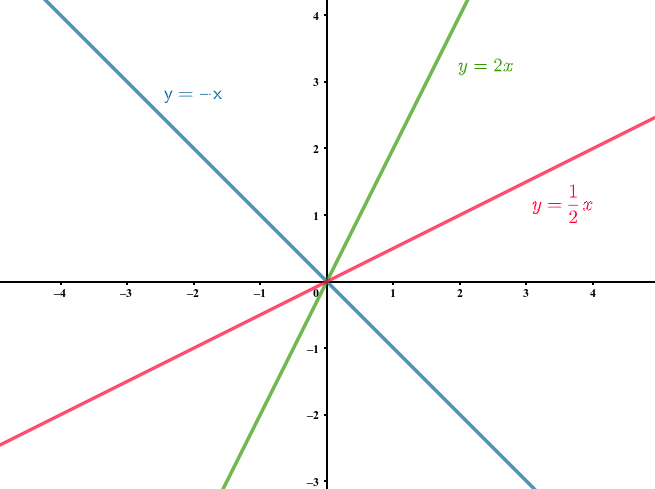
La representación gráfica de una función de proporcionalidad \(y=mx\) es una recta.
La recta siempre pasa por el origen de coordendas, como se puede observar en la gráfica.
En esta expresión \(m\) es la pendiente de la recta y muestra su inclinación, si \(m\) es positiva la función será creciente, si es negativa será decreciente. Mientras mayor sea \(m\) más inclinada estará la recta, en cambio si \(m\) es muy pequeño la inclinacición disminuye.
Función lineal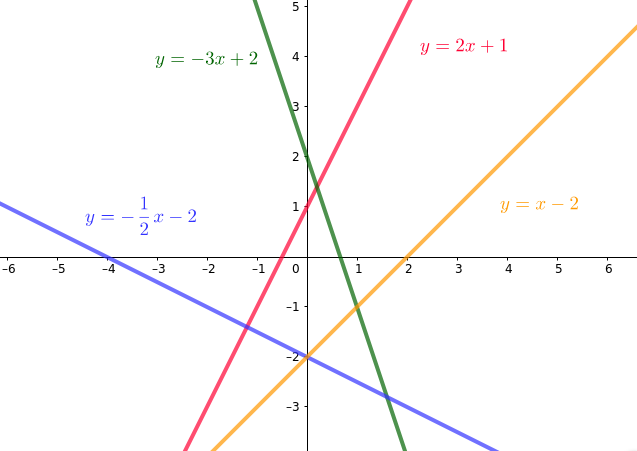 La gráfica de una función lineal \(y=mx+n\), al igual, que la función de proporcionalidad es una recta. Como se puede observar en la imagen. A diferencia de la primera la gráfica no pasa por el origen de coordenadas.
La gráfica de una función lineal \(y=mx+n\), al igual, que la función de proporcionalidad es una recta. Como se puede observar en la imagen. A diferencia de la primera la gráfica no pasa por el origen de coordenadas.
Fíjate en la expresión analítica que aparece junto a cada gráfica, ¿observas alguna relación entre el punto de corte de la gráfica con el eje de ordenadas y la expresión analítica?
Si no encuentras la relación no te preocupes en el siguiente apartado (corte con los ejes) tienes la respuesta.
Función de proporcionalidad
Como se ha visto en la gráfica la función de proporcionalidad pasará siempre por el origen de coordenadas \((0,0)\), esto se comprueba tomando la expresión analítica y sustituyendo en ella, si \(x=0\), entonces, \( y=mx \rightarrow y=m\cdot 0=0\).
Ejemplo:
Dada la función de ecuación \(y=3x\) determina los cortes con los ejes. Para \(x=0\) se tiene que \(y=3 \cdot 0 \rightarrow y=0\) luego corta los ejes en \((0,0)\).
Función lineal
Si has observado la gráfica de la función lineal, corta a los ejes en dos puntos, uno en el eje de ordenadas y otro en el eje de abscisas.
La función lineal, corta al eje de ordenadas (\(Y\)) cuando \( x=0 \rightarrow y=m\cdot 0+n=n\), lo hará en el punto (\(0,n)\) a este punto se le llama ordenada al origen. Basta con observar la gráfica para darse cuenta de que el corte coincide con el término independiente de la expresión analítica.
La función lineal cortará al eje de abscisas (\(X\)) cuando \(y=0 \rightarrow 0=mx+n \rightarrow mx=-n \rightarrow x=\dfrac{-n}{m}\). El punto de corte será \(\left(\dfrac{-n}{m},0\right)\).
Ejemplo:
Dada la función lineal \(y=2x+4\) vamos a determinar sus cortes con los ejes.
Corte con el eje de ordenadas: \(x=0\) entonces \(y=2·0+4 \rightarrow y=4\), el punto de corte será \((0,4)\).
Corte con el eje de abscisas: \(y=0 \rightarrow 0=2x+4 \rightarrow 2x=-4 \rightarrow x=\dfrac{-4}{2}=-2 \) luego el punto será \((-2,0)\).
Observa las siguientes gráficas y calcula los puntos de corte, comprueba tus cálculos con la gráfica 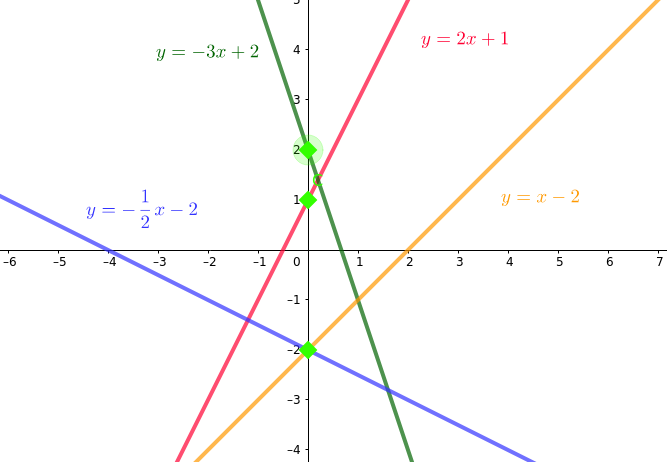
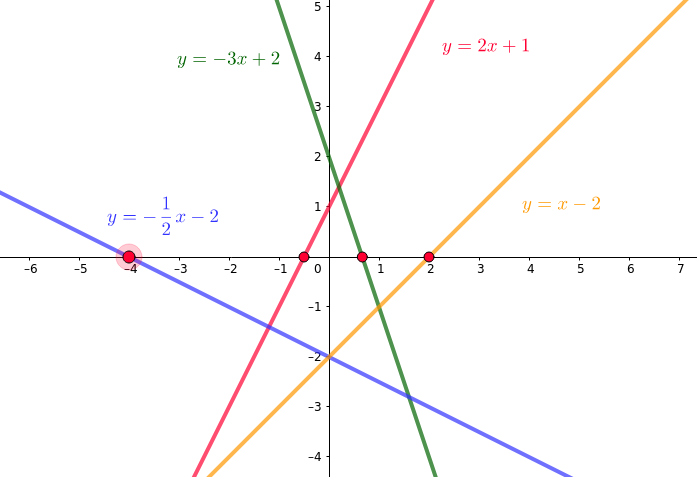
Una función de proporcionalidad o lineal será creciente cuando su pendiente sea positiva, en cambio, cuando la pendiente sea negativa será decreciente.
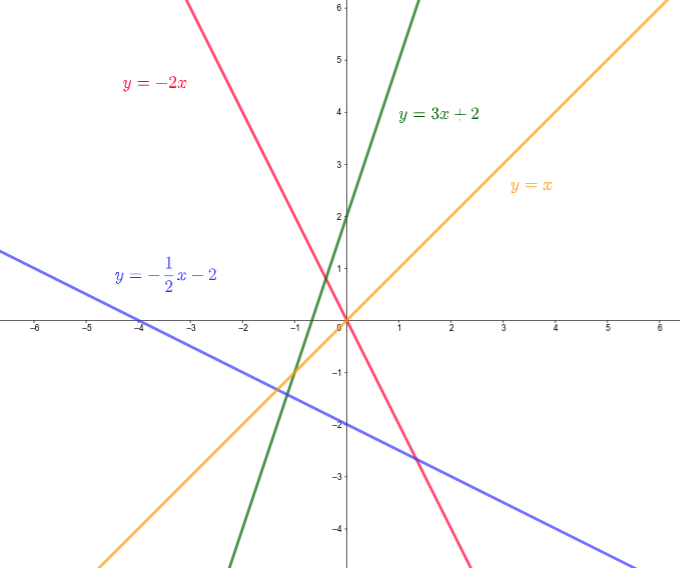
Observa las gráficas de las funciones que se muestran. Fíjate en la pendiente (es el coeficiente de la variable independiente). Cuando la pendiente es positiva, las funciones son crecientes, en cambio, cuando es negativa son decrecientes
El conocimiento del comportamiento de una función lineal y sus características es importante para comprender la relación entre dos magnitudes, con estas actividades se persigue que afiances ese conocimiento y obtengas soltura usándolas.
Responde a las siguientes preguntas.
Verdadero
Falso
Falso
Falso
Verdadero
Actividad de cuaderno
Observa a tu alrededor y encuentra dos magnitudes que se relacionen linealmente: una que siga una función de proporcionalidad y otra una función lineal.
Crea en ambos casos:
En el caso de la función de proporcionalidad
En el caso de la función lineal
¡Cuánto has aprendido hasta llegar aquí! ¿Verdad?
Todos estos aprendizajes te ayudarán, junto a otros, a resolver diferentes tareas y a desenvolverte en tu vida.
¿Qué estás aprendiendo? ¿Qué pasos has dado para llegar hasta aquí?
Reflexiona sobre ello un momento y completa el Paso 3 de tu Diario de Aprendizaje.
Cuando nos enfrentamos a una tarea nueva, podemos sentir muchas cosas:
Alegría, miedo, confusión, inseguridad, tensión, enfado, orgullo, …
Conocer qué sientes ante cualquier situación, te permitirá:
¡Oye tus emociones!
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0