.jpg)
Sucesión
Una sucesión es un conjunto de números reales que están escritos en orden, de modo que se puedan numerar sus posiciones: primero, segundo, tercero…
Ejemplos: a) 1, 3, 5, 7, 9, 11… b) 4, 8, 12, 16, 20… c) 1, 3, 9, 27, 81, 243…
Términos
Se llaman términos a los números que forman la sucesión y se suelen designar mediante una letra con subíndice. El primer término es \(a_1\), el segundo es \(a_2\), el tercero, \(a_3\)... El subíndice indica el lugar de cada término en la sucesión.
En cada caso particular, los términos de la sucesión son ciertos números reales (aunque también pueden ser letras o símbolos especiales).
En el ejemplo a) de antes, 1, 3, 5, 7, 9, 11… tenemos que \( a_1=1 ; \ a_2=3\ ,\ a_3=5... \)
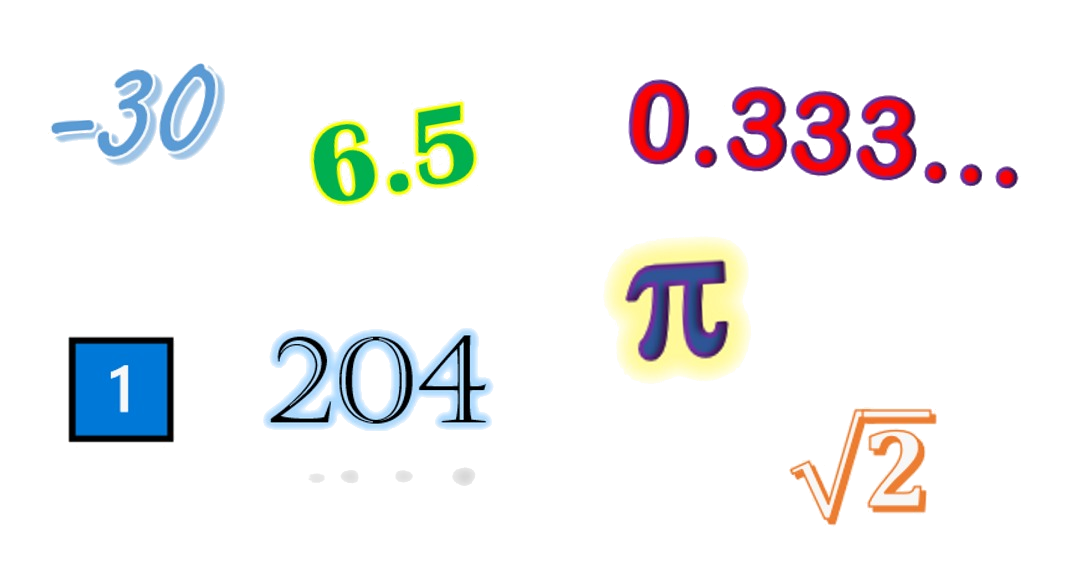
Definición
Conjunto de todos los números que conocemos. Comprende los enteros,>los que tienen decimales de cualquier clase , las fracciones, etc.
Ejemplo
1; 2; 6,5; 0,333...
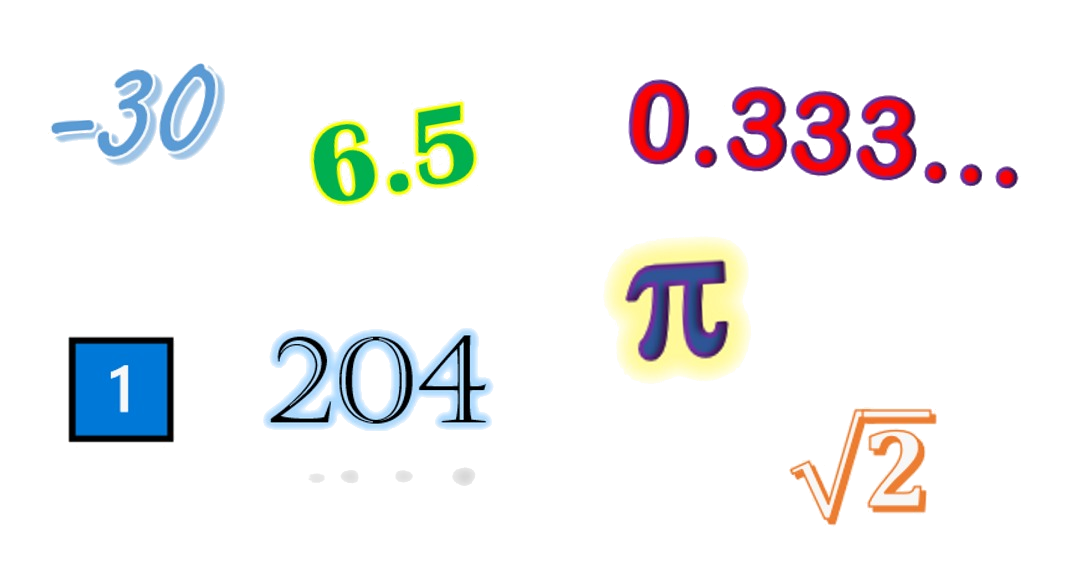

.jpg)
