Diccionario
Espesor

Paradoja histórica




Acabas de ver lo útiles que son las progresiones aritméticas en diferentes situaciones cotidianas entre las que se encuentran también acciones solidarias. Pero este no es el único tipo de sucesiones que te resultarán útiles para tu proyecto solidario. Como vas a poder comprobar en esta página, mediante las progresiones geométricas podrás describir muchas situaciones reales que podrás aplicar en tu proyecto.
Ya eres un experto en sucesiones. Así que vamos a intentar ampliar tus conocimientos. Observa la siguiente secuencia de números:
\( 3,9,27,81,243,.......\)
Ya sabes que los términos de las sucesiones los nombramos de la siguiente manera: \( a_{1}=3 \), \( a_{2}=9 \), \( a_{3}=27 \), \( a_{4}=81 \), \(a_{5}=243 \).....
¿Sabrías calcular \( a_{7}\)?
Observa que cada término se obtiene del anterior multiplicando por tres.
Esto dicho de otra manera, es: si dividimos un término concreto entre el inmediatamente anterior, obtenemos tres.
\( \dfrac{a_{2}}{a_{1}}=\dfrac{9}{3}=3 ; \dfrac{a_{3}}{a_{2}}=\dfrac{27}{9}=3 ; \dfrac{a_{4}}{a_{3}}=\dfrac{81}{27}=3 ;\dfrac{a_{5}}{a_{4}}=\dfrac{243}{81}=3 \)
Una sucesión cuyos términos se obtienen multiplicando por una cantidad fija r, se llama Progresión Geométrica de razón r.
En nuestro ejemplo, tendríamos una progresión geométrica de razón 3.
Como puedes observar, los términos de una progresión geométrica son infinitos.
Partiendo del primer término de una progresión geométrica a1, y conociendo la razón, podemos obtener los siguientes términos.
\( a_{1}= a_{1}\)
\( a_{2}= a_{1}·r\)
\( a_{3}= a_{2}·r=a_{1}·r^2\)
Si generalizamos esta secuencia, obtenemos: \( a_{n}= a_{1}·r^{n-1}\)
A esta expresión le llamamos término general de la progresión, ya que conociendo el primer término y la razón, podemos obtener cualquier otro.
Vamos a aplicar el término general que acabamos de aprender para calcular términos de la progresión.
\(\rightarrow \) Calcular el quinto término de una progresión geométrica de \( r=-2\) y \(a_{1}=5\)
El término general sería: \(a_{n}=5·(-2)^{n-1}\) , luego el quinto término: \(a_{5}=5·(-2)^{5-1}=5·(-2)^4=5·16=80\)
\(\rightarrow \) Calcular el primer término de una progresión geométrica de razón 4, cuyo cuarto término es 128.
El término general de esta progresión sería: \(a_{n}=a_{1}·4^{n-1}\) , luego el cuarto término:
\(a_{4}=a_{1}·4^{4-1}=a_{1}·4^3\)
Se indica que el cuarto término es igual a 128, luego: \(a_{4}=a_{1}·4^3=128\) \(\rightarrow \) \(a_{1}·64=128\)
expresión de la que se puede calcular el primer término: \( \dfrac{128}{64}=2\)
La progresión tendría el siguiente término general: \(a_{n}=2·4^{n-1}\)
\(\rightarrow \) La razón de una progresión geométrica también puede ser una fracción. Estudia el siguiente ejemplo:
Calcula el quinto término de una progresión geométrica de razón \( r=\dfrac{1}{2}\) y \(a_{1}=32\)
El término general de esta progresión sería: \(a_{n}=32·\left( \dfrac{1}{2} \right)^{n-1}\)
El quinto término lo podemos calcular de la siguiente manera:
\(a_{5}=32·\left( \dfrac{1}{2} \right)^{5-1}=32·\left( \dfrac{1}{2} \right)^4=32·\dfrac{1}{2^4}=32·32·\dfrac{32}{16}=2\)
En determinadas situaciones, puede resultarnos útil conocer la suma de los primeros términos de una progresión geométrica, por ejemplo los 10 primeros términos, o los 6 primeros términos. 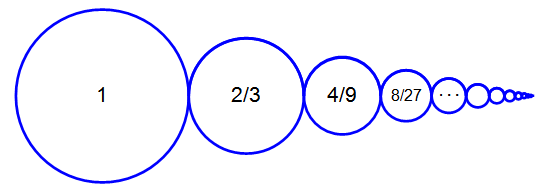
La expresión matemática para realizar este cálculo es: \(S_{n}=\dfrac{a_{1}·r^n-a_{1}}{r-1}\)
Si te ánimas y te interesa, un poco más abajo tienes la demostración detallada de esta expresión.
EJEMPLO
Calcular la suma de los 8 primeros términos de la progresión: 3,27,81,243,….
El primer término es 3, y la razón también es 3. Aplicando la expresión que acabamos de ver, nos queda:
\(S_{8}=\dfrac{3·3^8-3}{3-1}=\dfrac{3^9-3}{2}=\dfrac{59049-3}{2}=\dfrac{59049}{2}=29523\)
Como hemos visto, los términos de una progresión geométrica son infinitos.
¿Se puede realizar la suma de infinitos términos?
En general no podemos, recordemos la sucesión que estamos usando de ejemplo: 3,927,81,243,..... Si intentamos hacer la suma de “todos” los términos, el resultado sería infinito, pues cada vez se suma un término mayor al anterior.
Sin embargo, existe un tipo de progresiones geométricas, las que tienen razón entre -1 y 1. En estas sucesiones los términos son cada vez más pequeños. Observa la siguiente progresión, en la que el primer término es y la razón es \(r=\dfrac{1}{2}\).
10,5,2.5,1.25, 0.625, 0.3125, 0.15625,.......
Observa como los términos, aunque son infinitos, están cada vez más cerca de cero.
Esta circunstancia hace que sí se pueda obtener la suma de los infinitos términos.
La expresión matemática que nos da la suma de los infinitos términos de una progresión geométrica es:
\(S_{\infty}=\dfrac{a_{1}}{1-r}\)
los valores de r tienen que estar comprendidos entre -1 y 1. Es decir: \( -1\leq r \leq 1\)
EJEMPLO
Calcular la suma de todos los términos de la sucesión que tiene por término general: \(a_{n}=32·\left( \dfrac{1}{2} \right)^{n-1}\)
En está progresión el primer término es 32 y la razón, \(r=\dfrac{1}{2}\)
Por tanto, tenemos todos los elementos para calcular la suma de los infinitos términos:
\(S_{\infty}=\dfrac{32}{1-\dfrac{1}{2}}=\dfrac{32}{\dfrac{1}{2}}=64\)
_LACMA_M.73.5.586.jpg)
¿Te has preguntado alguna vez cómo surgió el ajedrez?
Cuenta una leyenda que hubo una vez un rey en la India que estaba tan triste por haber perdido a su hijo que nada lograba hacer olvidar esa pena.
Un buen día un hombre apareció en su corte y pidió audiencia. Cuando el rey lo recibió, el hombre le presentó al rey el tablero y las piezas. Además, le contó como se jugaba.
El rey, maravillado, comenzó a jugar hasta que consiguió olvidar su pena. Agradecido, mandó llamar al creador del juego, al que habló de esta forma:
- Quiero recompensarte por haber alejado de mi la pena por haber perdido a mi hijo. Soy un hombre rico, pídeme lo que quieras y te lo concederé.
- Majestad, grande es tu magnanimidad y quedo pagado con tu agradecimiento. Pero, si lo deseas...
- Pídeme lo que desees.
- Me gustaría pedirte un grano de trigo.
- ¿Sólo un grano de trigo?
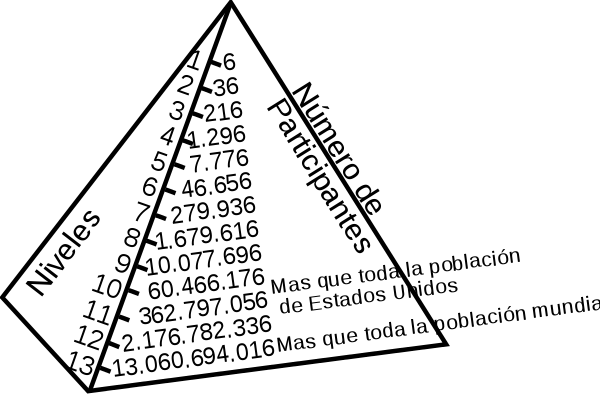
- No, un grano por la primera casilla, dos por la segunda, cuatro por la tercera, por la cuarta, ocho, y así sucesivamente.
El rey llamó a sus administradores para que calcularan la cantidad de granos de trigo que tendrían que entregarle al creador del juego. Pensaba que sería una cantidad pequeña pero quedó muy sorprendido al conocer la cantidad.
¿Le ayudamos a hacerlo?
Vamos a plantear la suma:
$ 1 + 2 + 4 + 8 + 16 + ... $
Si te das cuenta, los números anteriores pueden expresarse de la siguiente forma:
$ 2^{0}+2^{1} + 2^{2} + ... +2^{63} $
como ves, ¡se trata de una progresión geométrica!
Pero, ¿cómo podríamos calcular el total de granos que el monarca tiene que pagar? Para ello, podemos sumar todo lo anterior. O bien, pensando un poco, podemos hacer lo siguiente:
Vamos a llamar T al total de granos de trigo que tiene que pagar el rey. Fijate que T se calcula de la siguiente forma:
$ T = 2^{0}+2^{1} + 2^{2} + ... +2^{63} $ $[1]$
Si multiplicamos la expresión anterior por 2, quedaría:
$ 2T = 2^{1}+2^{2} + 2^{3} + ... +2^{64} $ $[2]$
Y, si ahora restamos a la expresión $ [2] $ la expresión $ [1] $, nos quedaría:
$ 2T - T = 2^{1}+2^{2} + 2^{3} + ... +2^{63} +2^{64} - 2^{0} - 2^{1} - 2^{2} - ... -2^{63} $
$ T = 2^{64} - 2^{0} $
$ T = 2^{64} - 1 $
Lo que hace un total de:
$ 18.446.744.073.709.551.615$
Si suponemos que en un kilo de trigo hay 25000 granos de trigo. ¿Cuántos kilos de trigo tendrá que pagar el rey al inventor del ajedrez?
Busca información de la producción mundial actual de trigo. ¿Podríamos pagar hoy la invención de dicho juego?
En los siguientes ejercicios vas a trabajar con las progresiones geométricas.
Veras como aplicarlas, las curiosidades que las rodean y como nos ayuda a resolver una paradoja histórica.

Hecho o dicho aparentemente contrario a la lógica.
Ejemplo¡Con cuántas paradojas históricas nos encontramos!
Observa el siguiente ejemplo:
El término general de una progresión geométrica es: \(a_{n}=3·4^{n-1}\)
Calcula los cinco primeros términos de la sucesión:
\(n=1 \longmapsto a_{n}=3·4^{1-1}=3·4^0=3·1=3\)
\(n=2 \longmapsto a_{n}=3·4^{2-1}=3·4^1=3·4=12\)
\(n=3 \longmapsto a_{n}=3·4^{3-1}=3·4^2=3·16=48\)
\(n=4 \longmapsto a_{n}=3·4^{4-1}=3·4^3=3·64=192\)
\(n=5 \longmapsto a_{n}=3·4^{5-1}=3·4^4=3·256=768\)
Es tu turno, utiliza la siguiente actividad interactiva para practicar.
Calcula en tu cuaderno los cinco primeros términos de las siguientes progresiones:
a) \(a_{n}=3·\left( \dfrac{2}{3} \right)^{n-1}\)
b) \(a_{n}=(-1)^{n-1}\)
c)\(a_{n}=3·6^{n-1}\)
d) \(a_{n}=0,1·\left( \dfrac{1}{10} \right)^{n-1}\)
Interactúa con la siguiente actividad para practicar el cálculo de términos de una progresión geométrica.
Calcula los términos de la progresión que faltan. Fíjate que primero debes de averiguar la razón.
Imagina que decides ayudar dos personas con algo que necesite realmente, por ejemplo a un compañero a entender un ejercicio difícil de matemáticas o a tu padre con las bolsas de la compra. La condición es que cada persona que ayudes, debe a su vez ayudar a dos más. Este proceso se podría definir como una cadena de ayudas y está muy relacionado con lo que hemos estudiado en esta unidad.
Responde a las siguientes preguntas:
Identificas alguna progresión en este enunciado.¿Cuál?
Describe sus características principales.
Calcula los 5 primeros términos.
Escribe el término general de la sucesión.
¿Cuántas células tenemos después de 10 generaciones?
Haz un dibujo que describa la situación que expresa el enunciado. A partir de él, asigna un valor de n a cada paso. ¿Identificas el patrón?
En este ejercicio vas a calcular el término general de la progresión conocidos varios términos términos.
a) Calcula el término general de una progresión geométrica en la que el primer término y cuarto término son: \( a_{1}=2, a_{4}=250\) .
b) Calcula el término general de una progresión en la que el primer término y cuarto término son: \( a_{1}=\dfrac{1}{2}, a_{4}=\dfrac{1}{16}\)
c) Calcula el término general de una progresión en la que el primer término y tercer término son: \( a_{1}=3, a_{3}=6\)
d) Calcula el término general de una progresión en la que el segundo término y cuarto término son: \( a_{2}=\dfrac{4}{9}, a_{4}=\dfrac{16}{54}\)
Prueba a seguir estos pasos:
1º Si conoces el primer término, es fácil ¿Puedes calcular la razón?
2º Si no conoces el primer término, tienes que aplicar el expresión del término general.
3º Tienes que aplicarlo dos veces, una vez por cada termino que conoces.
4º¿Puedes plantear un sistema de ecuaciones?

Aquiles, un valeroso guerrero Griego, es retado por una tortuga a una carrera. Por supuesto, Aquiles debe dejar algo de ventaja a la tortuga, pues como todo el mundo sabe, es mucho más lenta. La tortuga afirma que aunque Aquiles es más rápido, este nunca la alcanzará realmente, porque cuando llegue a dónde está la tortuga, esta ya habrá avanzado un poco de camino, por poco que sea. Cuando Aquiles recorra esa pequeña distancia, la tortuga habrá avanzado otro poquito, y así sucesivamente, por lo que nunca será alcanzada. ¿Está la tortuga en lo cierto?
Supón que Aquiles tarda en llegar a la posición inicial de la Tortuga 10 segundos y que luego tarda 1 segundo en alcanzar la 2ª posición y así sucesivamente.

¿Te has planteado alguna vez cuántas veces se puede doblar un papel?
Coge un folio y e intenta doblarlo varias veces. Antes de empezar, busca en internet el espesor que tiene un folio de tamaño A4. ¿Qué espesor tiene?
1. Al doblar una vez, ¿Qué espesor tiene el papel? ¿Y al doblarlo dos veces? ¿Y tres?
2. ¿Cuántas veces puedes doblarlo? ¿Qué espesor tiene el papel ahora?
3. Compara el espesor final con el original. ¿Crees que ha aumentado mucho o poco?
4. ¿Puedes explicar lo sucedido con alguna sucesión?. En caso afirmativo, escribe los términos
Ahora imagina que tienes un papel suficientemente muy muy grande. ¿Cuántos dobleces tendrías que hacerle para llegar a la Luna?
Ten en cuenta que la distancia de la Tierra a la Luna es de 384.400 Km

Grosor.
EjemploSu espesor no supera les 3 mm.
Piensa que conforme vas doblando, cada vez tienes más capas que doblar.
Con el primer doblez obtienes dos capas, con el segundo cuatro, y así sucesivamente.
Si ya has medido el espesor, ¿cómo va aumentando?
Escribe el número de capas que obtienes con cada doblez, seguro que identificas el tipo de progresión que se genera.
Seguro que mientras trabajabas, ha sucedido algo que te ha hecho parar.
Cuando aprendemos, estamos rodeados de cosas que nos pueden distraer.
Al volver a la actividad, nos cuesta volver a centrarnos.
Te voy algunos consejos para que te ayude a centrarte:
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0