Diccionario
Amontonar
.jpg "Amontonar")
Taller de joyas
4.2. Joyas cilíndricas
¿Recuerdas la investigación sobre el balón de fútbol? Seguro que muchas veces has tenido uno cerca y, quizás, no te habías fijado en que estaba formado por diferentes caras con forma de polígono.
Para diseñar nuestra joya podemos buscar inspiración en objetos de nuestro entorno.
¿Alguna vez has pensado qué tienen en común una lata de refresco, una vela o el rollo de papel higiénico?
Todos ellos son cilindros y tu joya podría tener esta forma.
Los cilindros son un tipo de prisma en particular, porque su base es un círculo.
¿Te gustaría aprender un poco más sobre ellos?
Lectura facilitada
Recuerda que para diseñar tu joya
has buscado la inspiración en los objetos del entorno.
¿Sabes que tiene en común una lata de refresco y una vela?
Estos dos objetos son cilindros.
Los cilindros son un tipo de prisma en particular, porque su base es un círculo.
Tu joya puede tener esta forma.
Vamos a aprender sobre los cilindros.
1. Cilindros
Cilindro
El cilindro es un caso especial de prisma en el que las bases son dos círculos.
En las siguientes pestañas veremos los elementos de un cilindro.
Bases
Los cilindros suelen estar apoyados sobre sus bases.
Las bases son los dos círculos y forman la cara superior y la cara inferior del cilindro.
Cara lateral
.gif "Caras laterales del cilindro")
La cara lateral es la que une las dos bases.
Esta cara tiene forma de rectángulo y se comprueba abriendo el cilindro y lo colocándolo plano.
Lo veremos en el apartado del área del cilindro.
Generatriz
.gif "Aristas de un prisma")
Como puedes ver, si haces girar un rectángulo alrededor de uno de sus lados, se genera un cilindro.
Llamamos generatriz a ese lado vertical del rectángulo que gira para crear el cilindro.
Altura
La altura de un cilindro es la distancia entre sus bases.
Aquí está representado el segmento que une las bases perpendicularmente.
¿Para qué sirven el área y volumen de los cilindros?
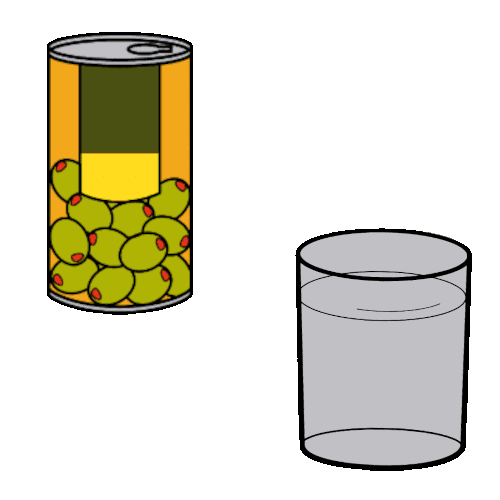
¿Reconoces estos objetos?
Todos son cilindros.
Para poder fabricar estos envases ha sido necesario calcular su área. De esta manera se obtiene la cantidad de material necesario para el envase.
¿Y qué representa el volumen del objeto? El volumen nos indica qué cantidad de producto vamos a poder guardar.
Como ves, el área y el volumen de estos cuerpos geométricos tiene aplicación en la vida real, en tu entorno.
Vamos a profundizar en ellos.
Área del cilindro
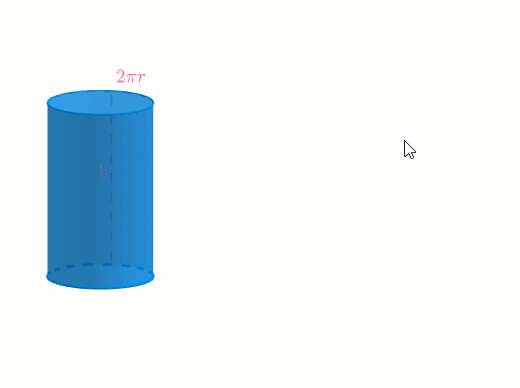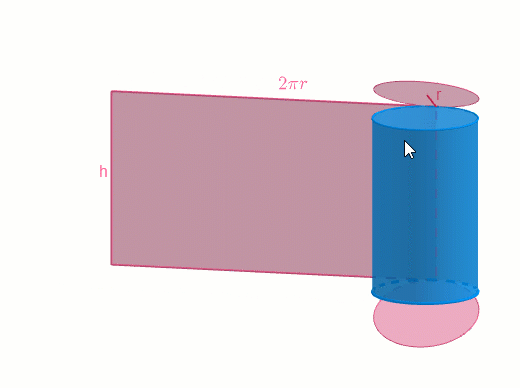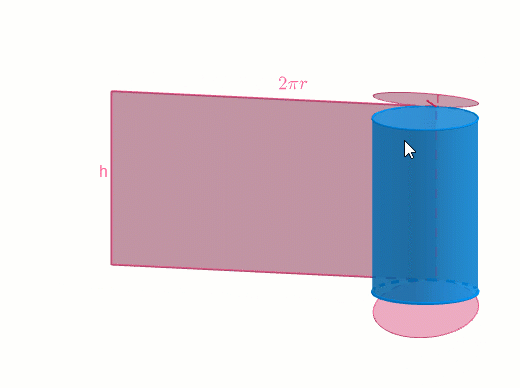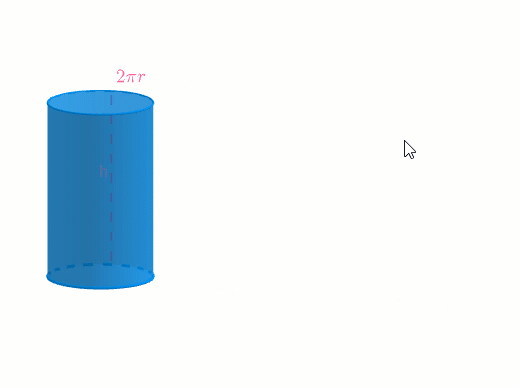
Esta imagen corresponde al desarrollo plano de un cilindro, es decir, el resultado de recortarlo y dejarlo plano. El área de un cilindro corresponde con la superficie de sus caras.
Para calcular el área total de este cilindro sumaremos las áreas de sus caras usando el desarrollo plano del cilindro. Como puedes ver, hay dos bases y una cara lateral, por tanto, podemos resumir los cálculos con la siguiente fórmula:
ÁREATOTAL= 2 · Áreabase + Árealateral
En las actividades lo trabajaremos paso a paso.
Volumen del cilindro
Como puedes ver, el cilindro se genera amontonando círculos.
El volumen de un cilindro es la cantidad de espacio que ocupa.
Por tanto, para calcular el volumen de un cilindro hay que multiplicar el área de la base por la altura, es decir, multiplicar el área de la base por el número de veces que se amontona.
El volumen se calcula de la siguiente manera.
VOLUMEN = ÁREAbase · altura
En las actividades lo trabajaremos paso a paso.
¿Qué significan estas fórmulas?
Como has podido ver, han aparecido varias fórmulas para calcular el área y el volumen de un prisma.
Para que una fórmula se más sencilla de aplicar, debe usar letras o palabras que representen los objetos implicados.
Por éso, para nombrar:
- el área de la base aparece Áreabase
- el área de la cara lateral aparece ÁREAlateral
2. Practicamos las áreas y volúmenes de los cilindros
En el proceso de diseño de tu joya tendrás que calcular su área y su volumen.
Comienza practicando con las áreas y volúmenes de los cilindros antes de diseñar una joya más compleja.
Puedes hacerlo de diferentes formas: de forma manipulativa construyendo cilindros, creándolos con GeoGebra, realizando los cálculos paso a paso, investigando en algunos objetos o, incluso, descubriendo otros nuevos con forma de cilindro.
Elige las actividades que mejor se ajusten a tí.
Lectura facilitada
Para diseñar tu joya tienes que calcular su área y su volumen.
Vas a practicar con el área y el volumen de un cilindro.
Ello te ayudará a diseñar tu joya.
Puedes hacerlo de diferentes formas:
- De forma manipulativa construyendo cilindros
- Creándolos con GeoGebra
- Realizando los cálculos paso a paso
- Investigando en algunos objetos
- Descubriendo otros nuevos con forma de cilindros.
Elige las actividades que mejor se ajusten a tí.
Opción A. Construye joya con forma de cilindro
Ha llegado el momento de diseñar tu propia joya usando cilindros.
Puedes hacerlo usando GeoGebra o a mano.
Después, usa la ficha adjunta para calcular su área y volumen.
¿Prefieres usar GeoGebra para construir la joya?
Construye en el siguiente applet el cilindro que se indica.
Pulsa en la vista gráfica que te interese para activar sus herramientas.
Puedes construirlo siguiendo las instrucciones del vídeo o con la herramienta Cilindro desde su base.
A continuación, usa la ficha adjunta para calcular su área y su volumen.
Puedes comprobar tus cálculos activando el rótulo de los objetos.
Ésta es la ficha para calcular el área y el volumen del cilindro que hayas construido.
¿No tienes acceso a internet o prefieres hacerlo a mano?
Si no tienes acceso a internet, puedes crear el tuyo propio usando cartulina.
En la siguiente ficha puedes elegir el que más te guste de los que aparecen.
Una vez que lo hayas construido, comprueba sus medidas reales con las que se indican en la ficha.
Si no tienes acceso a internet o prefieres dibujarlo a mano, aquí tienes una plantilla que te puede ayudar:
Opción B. Completa los cálculos en estos cilindros
Opción C. Investiga el área y volumen en estos cilindros
Vamos a comprobar lo que hemos aprendido con objetos de nuestro entorno.
En la siguiente actividad interactiva aparecerán ejemplos de actividades para practicar el cálculo de áreas y volúmenes de cilindros.
¿No tienes acceso a internet o prefieres hacerlo a mano?
Si no tienes acceso a internet o prefieres hacerlo a mano, puedes usar la siguiente ficha.
En ella aparecen tantas actividades como las que te saldrían en el juego anterior. Realiza las que necesites hasta que compruebes que lo dominas.
Opción D. Buscando cilindros en el entorno
Ha llegado el momento de investigar en el entorno.
Busca objetos que tengan forma de cilindro para poder estudiarlos.
Mídelos y calcula su área y su volumen.
Analiza si tus medidas y cálculos corresponden con su etiqueta.
Cuando termines, elabora un informe que recoja todo el proceso:
- qué objeto has elegido y por qué
- qué dimensiones tiene
- cómo has calculado su área y volumen
- ¿corresponden con las de su etiqueta?
Puedes elaborar el informe en el modo que más cómodo te resulte: en papel, presentación interactiva...
¿Quieres usar una plantilla para el informe?
Esta plantilla te puede servir para elaborar el informe que recoja todo el proceso.
¿Tienes dificultades para elaborar un documento?
La siguiente guía puede ayudarte a elaborar tu informe de forma digital.
Motus dice ¿Cómo se te ha dado la actividad?
¿Has tenido algún problema a la hora de realizar la actividad?
Cuando aprendemos algo nuevo es normal sentirse inseguro e incluso equivocarle, todo ello forma parte de aprender algo.
¿Recuerdas algo que te costase mucho esfuerzo, como por ejemplo montar en bicicleta?
Seguro que fue difícil pero con constancia lo conseguiste. Pues cada error que cometas te va a servir para aprender y mejorar para la siguiente vez que nos ocurra.
Para aprender de tus errores sigue estos consejos:
1. Me doy cuenta de en qué parte he fallado.
2. Busco la forma de mejorar ese error.
3. Lo intento de nuevo.
4. Entiendo que el error es importante para aprender.
No lo olvides: cuando te equivocas una vez, aprendes para el siguiente intento.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0