Diccionario
Consecutivas

Definición:
Que va en orden, se produce inmediatamente después.
Ejemplo:
Lunes y martes son días consecutivos.

Definición:
Que va en orden, se produce inmediatamente después.
Ejemplo:
Lunes y martes son días consecutivos.

¿Recuerdas cuándo nos dieron el plano del laberinto reflejado en un espejo?
Para dibujar la solución se usó una línea como referencia.
La figura inicial y la solución estaban a la misma distancia de esa línea.
Pues ahí ya estabas usando la simetría axial y no te estabas dando cuenta.
Aquí aprenderás a usarla correctamente lo que te permitirá que nuestro puzzle quede mucho más bonito.
Una simetría axial es un movimiento en el que la distancia al eje de simetría de cada uno los puntos de la figura inicial y de la simétrica es a la misma.
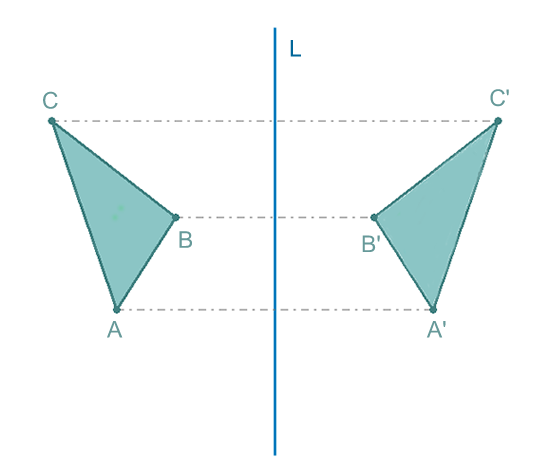
Para que sea más sencillo, primero vamos a ver la simetría entre puntos, que nos permitirá entender la simetría axial de las figuras. Como podéis observar, la distancia de los puntos iniciales con respecto al eje es la misma que la distancia de los puntos simétricos con respecto al eje.
rapido.gif)
Una vez que hemos visto la simetría axial entre puntos, para realizarla con figuras se hace de la misma manera:
rapido.gif)
Recuerdas que para solucionar el plano del laberinto
Reflejado en un espejo
Usaste una línea como referencia.
Y que la figura inicial y la solución
estaban a la misma distancia de la línea.
En ese momento estaba usando la simetría
Concretamente la simetría axial.
¡Adelante!
La simetría axial es un movimiento que se muestra en torno a un eje.
Cada uno de los puntos simétricos
de la figura inicial y de la figura simétrica
están a la misma distancia del eje.

Primero vamos a ver la simetría entre puntos
que nos permitirá entender la simetría axial de las figuras.
Como puedes ver, la distancia de los puntos iniciales
con respecto al eje es la misma
que la distancia de los puntos simétricos con respecto al eje.
.gif)
Una vez que hemos visto la simetría axial entre puntos,
para realizarla con figuras se hace de la misma manera:
.gif)
Si no manejas GeoGebra, este vídeo te servirá de ayuda:

En las siguientes actividades continuaremos explorando las simetrías axiales en figuras.
Algunas actividades son interactivas y en otras puedes elegir hacerlas en papel o con GeoGebra.
En algún apartado, incluso puedes usar otros materiales.
Elige en cada caso la que prefieras.
Vamos a practicar las simetrías axiales.
Imagina que a la primera figura se le han colocado espejos sobre las líneas naranjas.
Arrastra a los huecos las figuras que cumplan que se ha realizado la simetrías en esas líneas naranjas.
Ha llegado el momento de crear tu propio mosaico usando simetrías axiales.
Aquí tienes paso a paso la construcción del mosaico usando simetrías axiales:
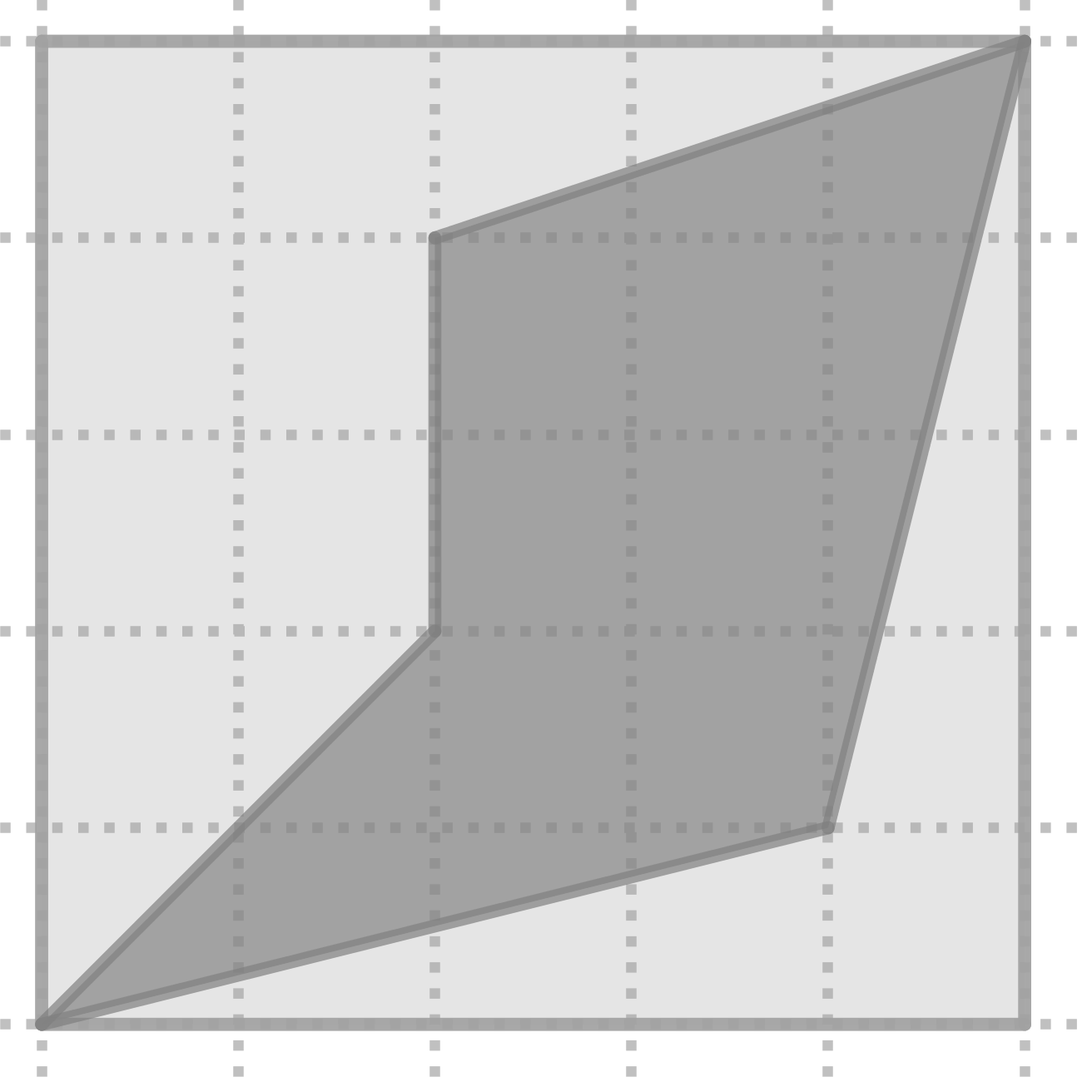
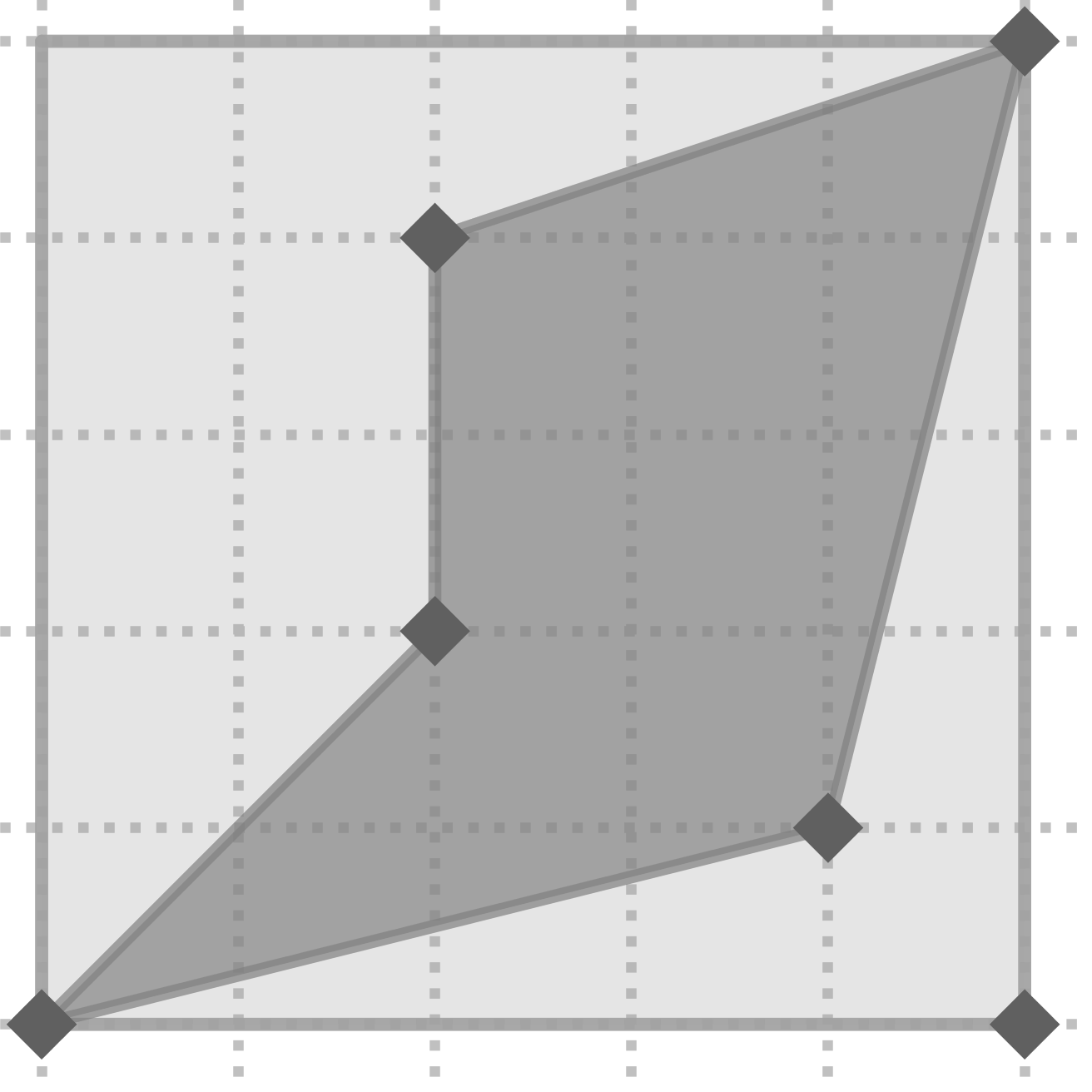
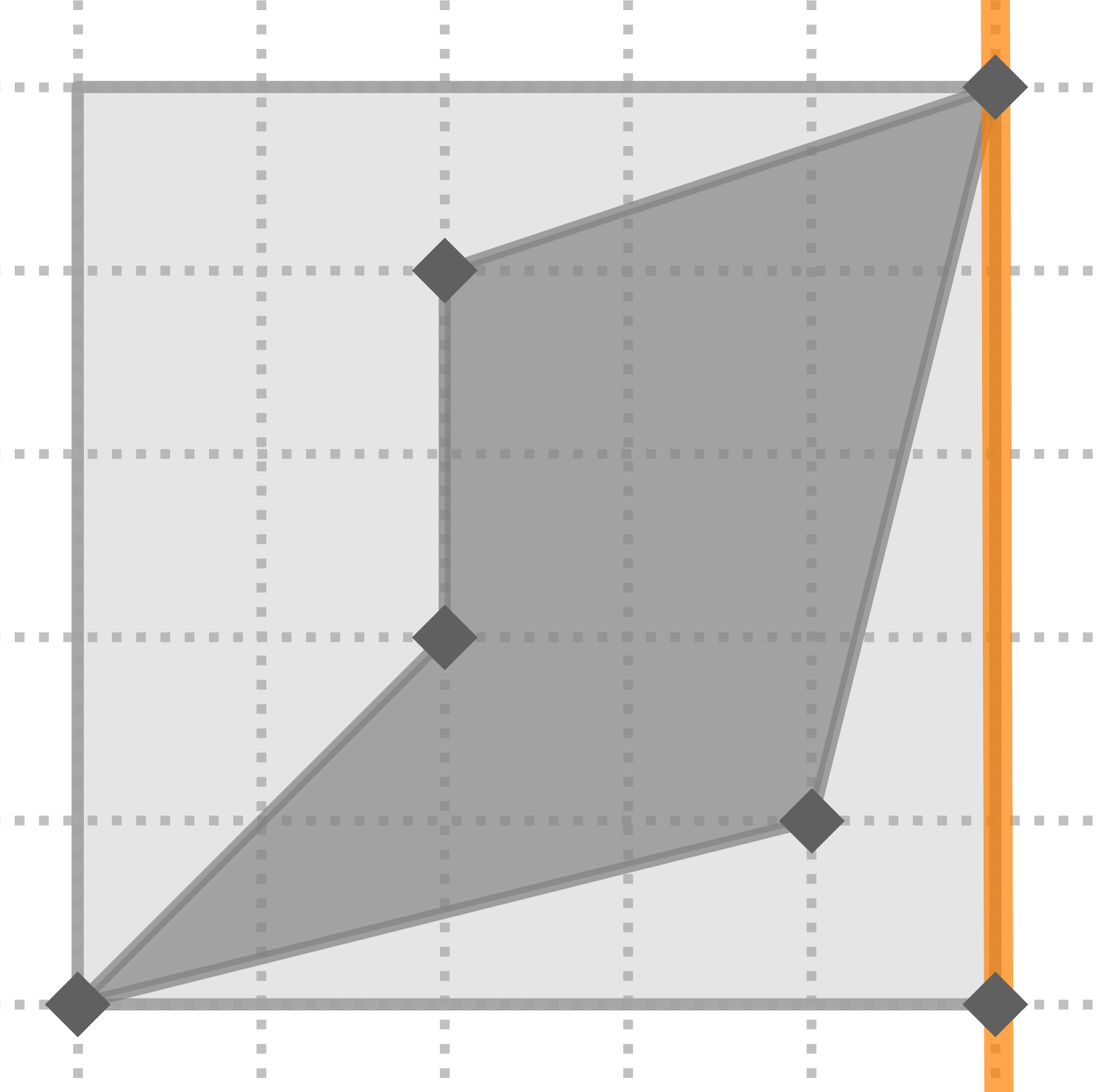
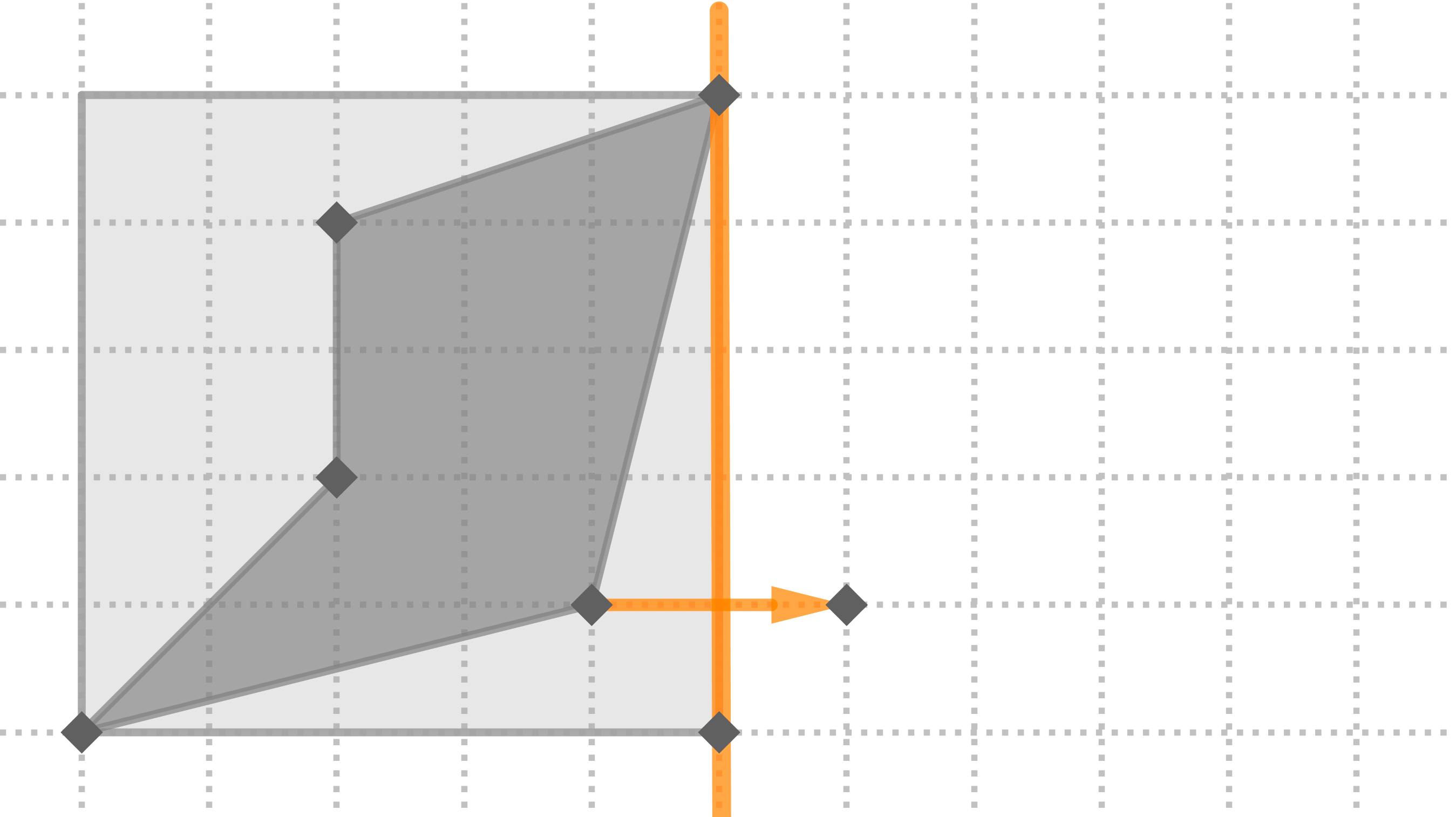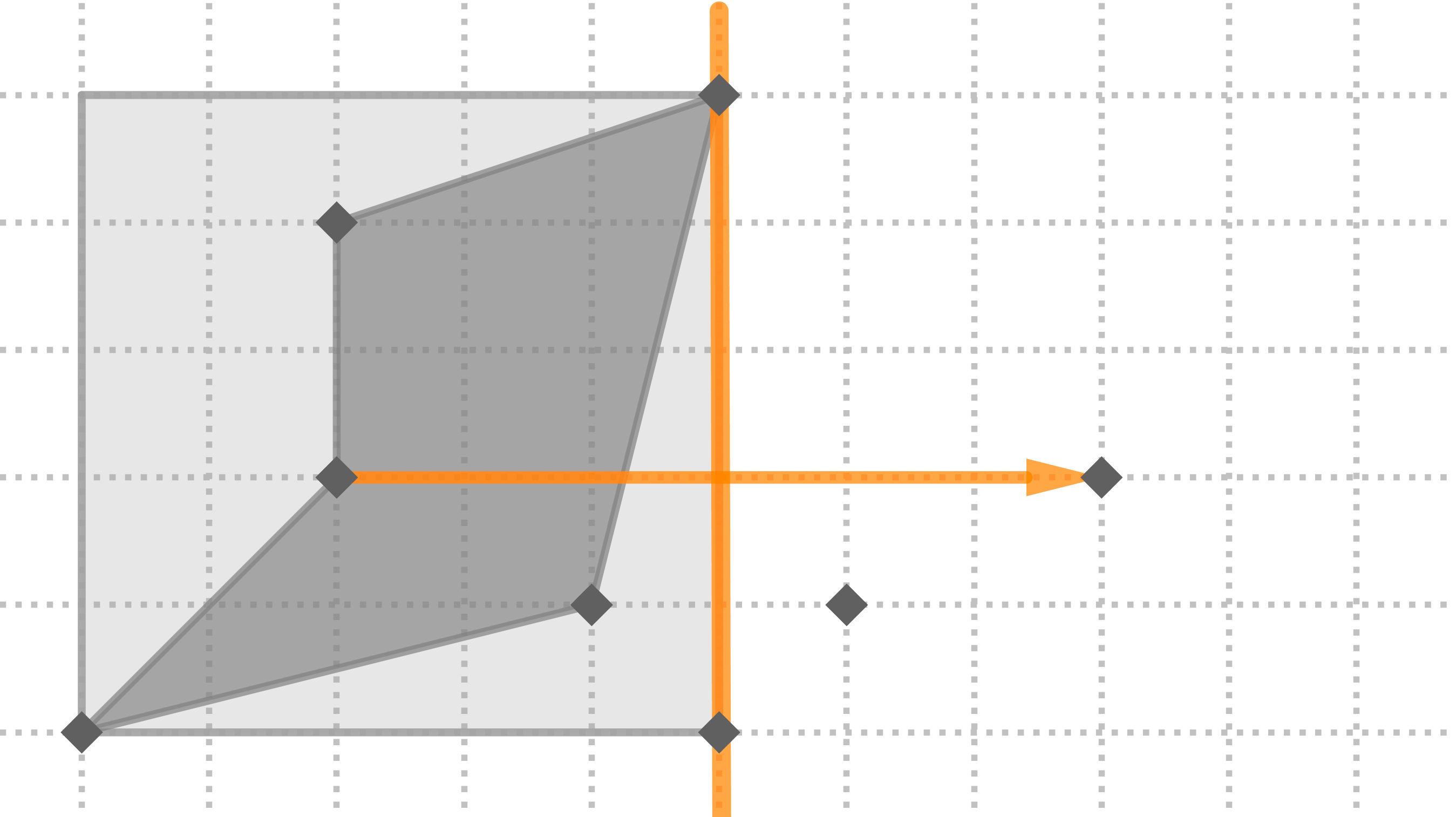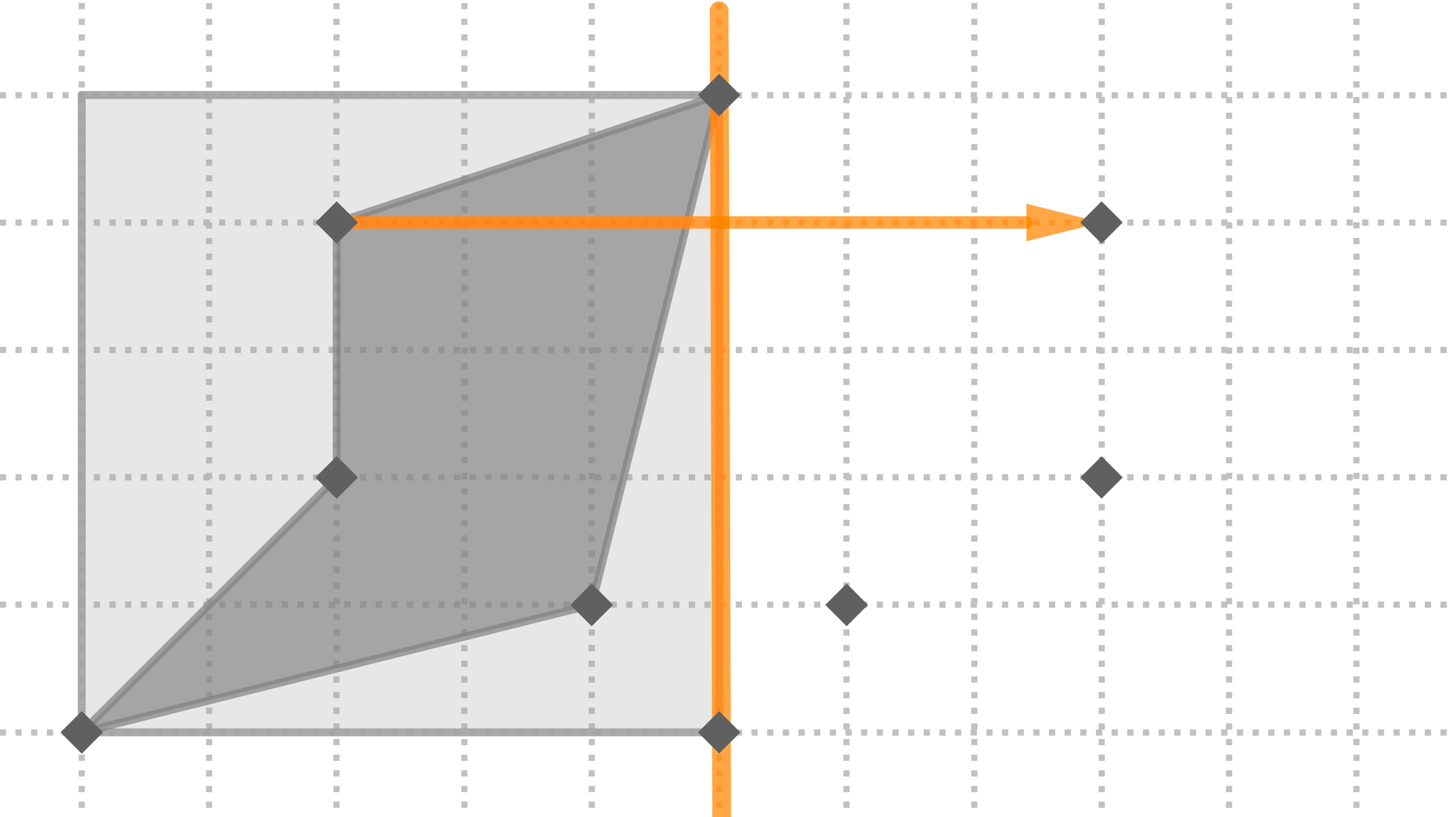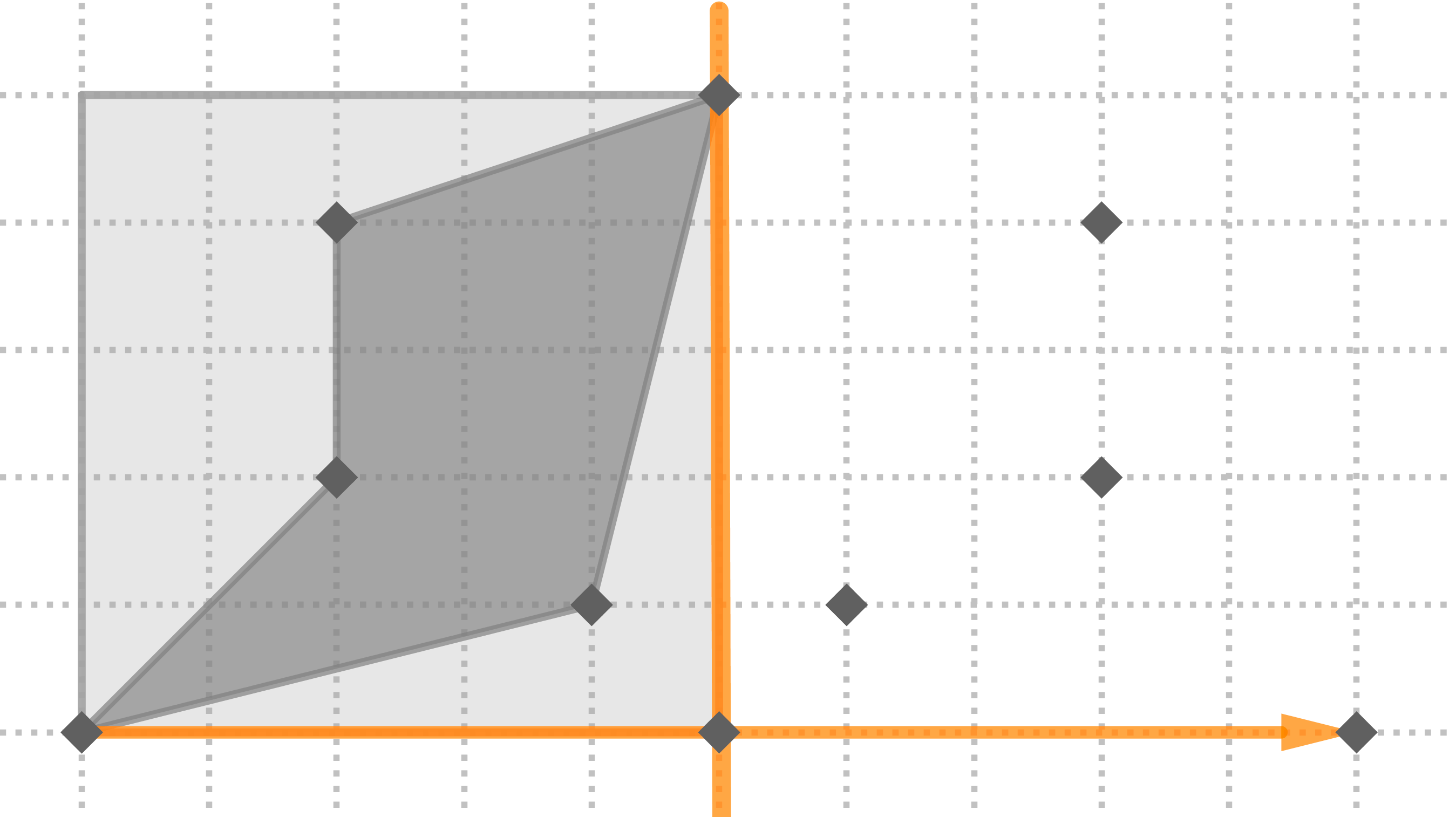
Aquí la tienes dibujada con la cuadrícula de fondo o sin ella:
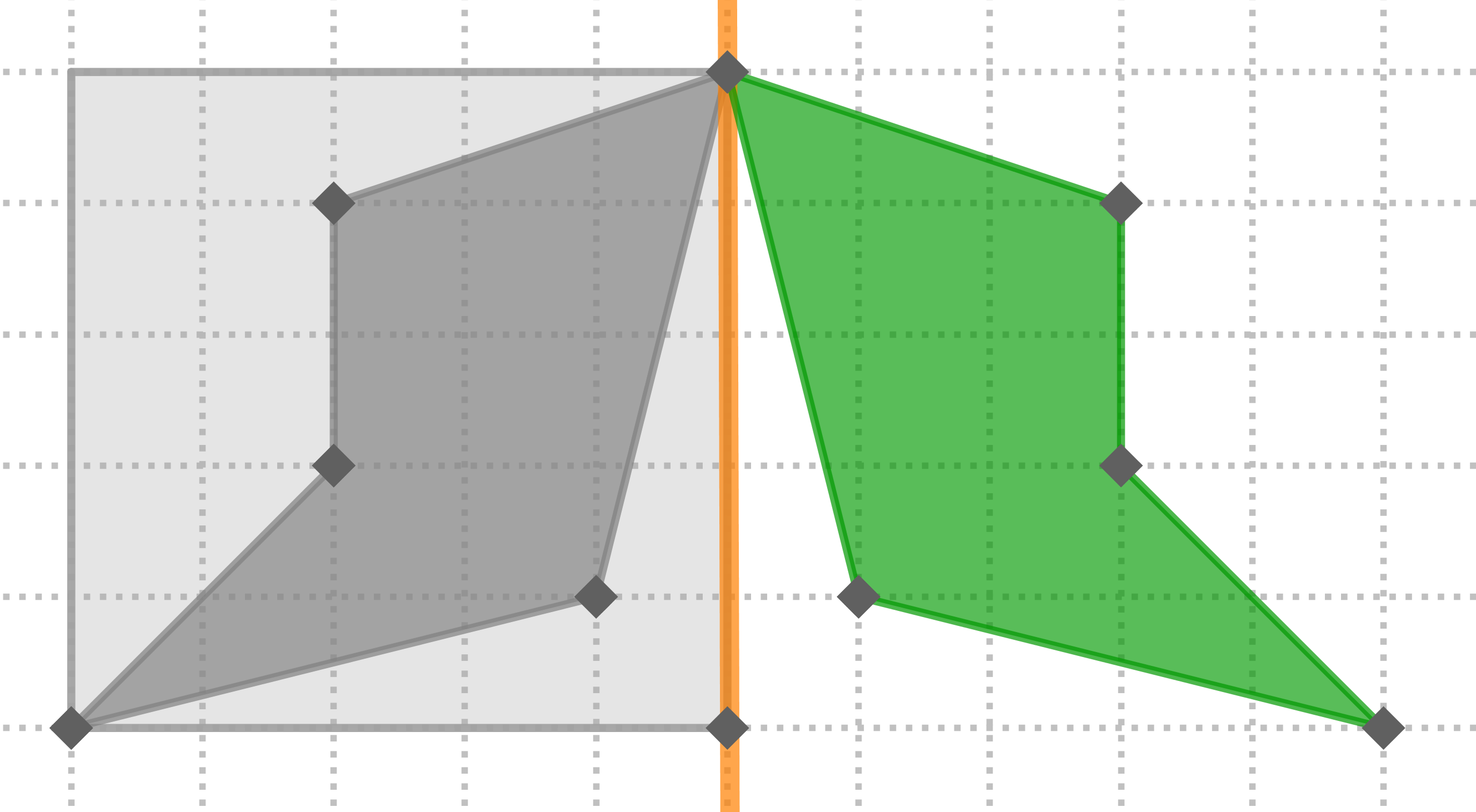


¡Es tu turno!
Puedes crear tu mosaico aplicando simetrías axiales a la siguiente figura.
Al inicio de la página aparece un vídeo explicativo de uso de GeoGebra para realizar simetrías axiales.
Usa las herramientas que aparecen en la parte superior para crear la simetría axial tal y como se explica en el vídeo.
Para que el resultado sea más atractivo, modifica los colores de las figuras que vayas creando.
Si no tienes acceso a internet o prefieres dibujarlo a mano, aquí tienes una plantilla que te puede ayudar:
¡Es tu turno!
Puedes crear tu mosaico aplicando simetrías axiales a la siguiente figura.
Al inicio de la página aparece un vídeo explicativo de uso de GeoGebra para realizar simetrías axiales.
Usa las herramientas que aparecen en la parte superior para crear la simetría axial tal y como se explica en el vídeo.
Para que el resultado sea más atractivo, modifica los colores de las figuras que vayas creando.
Si no tienes acceso a internet o prefieres dibujarlo a mano, aquí tienes una plantilla que te puede ayudar:
Ha llegado el momento de crear tu propio mosaico usando simetrías axiales.
Puedes hacerlo a mano, con GeoGebra o con otros materiales como plastilina, arcilla, madera o lo que se te ocurra.
Añade una ficha donde expliques cómo has diseñado la figura inicial y cómo has completado el mosaico.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0