Diccionario
Instruir
- Definición:
-
Proporcionar conocimientos, habilidades, ideas o experiencias a una persona para darle una determinada formación.
- Ejemplo:
-
Voy a instruirte en técnicas de ajedrez.
Crea tu emblema numerorum
4.3 Entrena el Poder de las Raíces
Diccionario
Instruir
Raíces
El poder de la Potencia es asombroso y parece incontrolable, por eso te instruiré en el arte de su control.
Recuerdas cuando queríamos reducir a la mitad el número de pasos, uniendo los núcleos que habíamos dividido. En ese caso pasábamos de 65.536 a 256. Pues lo que estábamos haciendo entonces era una raíz cuadrada.
La raíz cuadrada de un número, es otro número que al elevarlo al cuadrado nos da el primero. En nuestro caso 2562 = 65.536 , por eso la raíz cuadrada de 65.536 es 256.
El símbolo que se utiliza es √
Así que \( \sqrt{65536} \) quiere decir, la raíz cuadrada de 65536.
\( \sqrt{65536} = \) 256
Radicando
El radicando de una raíz es el número al que queremos calcular la raíz cuadrada.
Índice
La raíz cuadrada se puede ver como la operación opuesta al cuadrado.
Por eso se dice que el índice de la raíz cuadrada es 2, y debería escribirse arriba a la izquierda así: 2√
pero cómo es la raíz más usada, no se pone.
Raíz cuadrada exacta
Cuando tenemos un cuadrado perfecto, la raíz cuadrada va a salir un número entero y por eso se llama exacta.
Ejemplo:
La raiz cuadrada de 144 va a ser exacta, porque 144 es un cuadrado perfecto.
144 = 12•12
Por tanto, la raíz cuadrada exacta de 144 es 12
Raíz cuadrada entera
Si queremos obtener la raíz cuadrada de un número que no sea cuadrado perfecto, no va a ser tan fácil, pues el resultado no será un número entero.
Se llama raíz cuadrada entera al mayor número cuyo cuadrado es menor que que el radicando.
Por ejemplo:
La raiz cuadrada entera de 72 es 8, ya que \(8^2 = \) 64 < 72 < 81 = \( 9^2 \)
Aproximación de una raíz
Si queremos calcular una raíz cuadrada que no es exacta podemos hacerlo por aproximación.
Por ejemplo:
Si queremos calcular \( \sqrt{30} \), sabemos que no será un número entero, pero al menos podemos saber entre que números estará comprendida:
5 < \( \sqrt{30} \) < 6 porque \(5^2 = \) 25 < 30 < 36 = \( 6^2 \)
Raíz de una multiplicación.
Si tenéis que hacer la raíz a una multiplicación, se puede hacer de dos formas:
- Hacéis la multiplicación y luego la raíz, o
- Hacéis la raíz a cada factor y luego multiplicáis las raíces.
Ejemplo:
a) \(\sqrt{2 \cdot 8} = \sqrt{16} = 4 \)
b) \(\sqrt{4 \cdot 25} = \sqrt{4} \cdot \sqrt{25} = 2 \cdot 5 = 10 \)
Parece que la primera forma va a ser siempre más sencilla y la segunda es más complicada, pero si queréis usar la Magia de la Simplificación la segunda será la que necesitéis. Cuando estéis en el mundo de las ecuaciones no podréis usar la primera forma muchas veces.
Raíz de una división. Raíz de una fracción
Si tenéis que hacer la raíz a una división, se puede hacer de dos formas:
Hacéis la división y luego la raíz, o
Hacéis la raíz a cada factor y luego dividís las raíces.
Ejemplo:
a) \(\sqrt{27 / 3} = \sqrt{9} = 3 \)
b) \(\sqrt{16 / 25} = \sqrt{16} / \sqrt{25} = 4/5 \)
Parece que la primera forma va a ser siempre más sencilla y la segunda es más complicada, pero si queréis usar la Magia de la Simplificación la segunda será la que necesitéis. Cuando estéis en el mundo de las ecuaciones no podréis usar la primera forma muchas veces. Además este truco os permitirá hacer la raíz de una fracción:
Para realizar la raíz de una fracción:
Hacemos la raíz del numerador, y ese será el nuevo numerador.
Hacemos la raíz del denominador, y ese será el nuevo denominador.
Ejemplo:
\(\sqrt{49/25} = \sqrt{49} / \sqrt{25} = 7/5\)
Lectura facilitada
El poder de la Potencia es asombroso y parece incontrolable, por eso te enseñaré el arte de su control.
Para controlarlo usarás las raíces cuadradas.
Las raíces cuadradas son operaciones matemáticas
donde tendrás que encontrar un número multiplicado por sí mismo.
Ese número te dará el resultado.
El símbolo que se utiliza es √
Por ejemplo la raíz cuadrada de 16 es 4.
Porque 4•4 es 16.
√16= 
En las raíces cuadradas la operación opuesta es la potencia al cuadrado.
Igual que la multiplicación y la división son operaciones opuestas.
En esta raíz cuadrada √16 hay dos elementos:
Radicando
El radicando de una raíz es el número al que queremos calcular la raíz cuadrada.
En nuestro caso es el número 16.
Índice
La raíz cuadrada se puede ver como la operación opuesta al cuadrado.
Por eso el índice de la raíz cuadrada es 2.
Se debería escribir arriba a la izquierda así: 2√
pero cómo es la raíz más usada, no se pone.
Raíz cuadrada exacta
Cuando tenemos un número elevado al cuadrado
la raíz cuadrada va a ser exacta.
Esto se llama también cuadrados perfectos.
Por ejemplo la raíz cuadrada de 16 es 4 porque 4•4
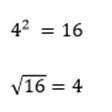
La raíz cuadrada exacta de 16 es 4.
Raíz cuadrada entera
Muchos números no tienen raíz cuadrada exacta.
Son los números que no son cuadrados perfectos.
Cuando esto ocurre calculamos la raíz cuadrada entera.
Por ejemplo 20 no tiene raíz cuadrada exacta porque no es un cuadrado perfecto.
Lo que se hace es buscar el número que más se acerque a 20 sin pasarse.
Los números que más se acercan a 20 son 4 • 4 = 16 y 5 • 5 = 25
La raíz cuadrada entera de 20 es 4.
Porque 16 es el cuadrado que más se acerca a 20 sin pasarse.
Aproximación de una raíz
Hay raíces que no son exactas.
Cuando hay una raíz que no es exacta puedes calcularla por aproximación.
Por ejemplo:
Si quieres calcular 
no te dará exacta.
Pero sabemos que estará entre dos raíces como son:
= 5
= 6
Entonces la quedará así:
5 < < 6
esto es así porque:
52 < 30 < 62
25 < 30 < 36
30 es un numero aproximado a 25 y a 36.
Raíz de una multiplicación.
Para realizar la raíz de una multiplicación hay dos formas:
Por ejemplo para la raíz de √8 • 2 =
1. Haces primero la multiplicación y luego la raíz.
√8 • 2 = √16 = 4
2. Haces la raíz de cada número (factor) y luego multiplicas las raíces.
√8 • 2
√8 • √ 2 = √16 = 4
Raíz de una división. Raíz de una fracción
Raíz de una división:
Para realizar la raíz de una división hay dos formas:
Por ejemplo para 
1. Haces la división y luego la raíz cuadrada.
2. Haces la raíz de cada número y luego resuelves la división de raíces.
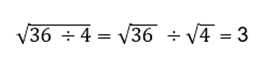
Raíz de una fracción:
Para realizar la raíz de una fracción hay dos formas.
Por ejemplo para la raíz de 
Hacemos la raíz cuadrada del numerador.
Hacemos la raíz cuadrada del denominador.
Por último resolvemos.
Entrena el Poder de las Raíces
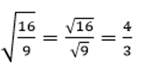
Ahora tendrás que poner en práctica tus poderes sobre operaciones con raíces, con ayuda de las siguientes actividades.
Opción A: Usa tu magia
La raíz cuadrada exacta de un número a es otro número b, cuyo cuadrado es igual al primero:
\( \sqrt{a} = b \) cuando \( b^2 = a \)
Por ejemplo:
- \( \sqrt{25} = 5 \) porque \( 5^2 = 25 \)
- \( \sqrt{36} = 6 \) porque \( 6^2 = 36 \)
- \( \sqrt{121} = 11 \) porque \( 11^2 = 121 \)
Al signo \( \sqrt{ } \) se le llama radical. Al valor que hay dentro del radical se le llama radicando.
Botón de la Insignia del Topacio
Si has superado el reto, has conseguido la Insignia del Topacio. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción B: Practica tu poder
Botón de la Insignia del Diamante
Si has superado el reto, has conseguido la Insignia del Diamante. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción C: Aplica tu poder
Observa este bonito reloj de pared, donde cada hora es marcada utilizando una raíz:
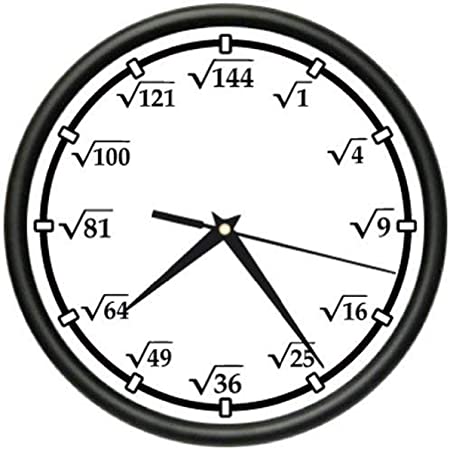
Si queremos hacer un regalo especial, más personalizado, utilizando productos y cocientes de raíces. Ya tenemos preparadas todas las cuentas. Solo nos falta que nos ayudes a ordenarlas, de forma que el primer valor marque la una, el segundo valor marque las 2,...
- \( \sqrt{25/25} \)
- \( \sqrt{16} / \sqrt{4} \)
- \( \sqrt{36} / \sqrt{4} \)
- \( \sqrt{4} * \sqrt{4} \)
- \( \sqrt{1} * \sqrt{25} \)
- \( \sqrt{36} / \sqrt{1} \)
- \( \sqrt{343} / \sqrt{49} \)
- \( \sqrt{128/2} \)
- \( \sqrt{405/5} \)
- \( \sqrt{100} / \sqrt{1} \)
- \( \sqrt{11} * \sqrt{11} \)
- \( \sqrt{12} * \sqrt{12} \)
Botón de la Insignia del Diamante
Si has superado el reto, has conseguido la Insignia del Diamante. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción D: Analiza usando tu poder
Disponemos de 89 baldosas cuadradas para hacer un mosaico cuadrado imitando al de la siguiente figura:
Botón de la Insignia del Ilustrador
Si has superado el reto, has conseguido la Insignia del Ilustrador. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción E: Crea con tu poder
Ahora toca demostrar que dominas el mundo de las raíces.
Para ello necesitarás diseñar un regalo, parecido al ejemplo del reloj, pero esta vez, en lugar de usar raíces exactas, deben ser aproximaciones.
Una vez que lo hayas terminado, explica al resto de la clase cómo lo has desarrollado y qué camino propones para resolverlo.
Recuerda que tu regalo no tiene por qué ser un reloj. ¡¡¡Cuanto más original sea, más gustará a tus amigos!!!
Botón de la Insignia del Zafiro
Si has superado el reto, has conseguido la Insignia del Zafiro. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Fin de actividad multinivelada
Ya has practicado tu Poder de la Raíz, y ahora podrás usarlo en la vida cotidiana para resolver problemas.
Con las insignias que hayas conseguido servirán para crear vuestro Emblema.
Botón de la Insignia de las Raíces
Podréis conseguir la maravillosa Insignia de las Raíces para vuestro grupo cuando acabéis vuestro adiestramiento.
¿Cuánto sabéis?
¿Cuánto saben tus compañeros o compañeras?
En esta actividad grupal vamos a intentar que observes a tu grupo y te fijes en todo lo que sabe sobre el tema que estáis viendo.
Cuando trabajamos en grupo aprendemos todos de todos.
Hay compañeros que recuerdan muchas cosas, otras que hablan muy bien, otros que son muy habilidosos con las manos o con los pies, otras dibujan estupendamente… Todos tenemos superpoderes para resolver las actividades, pero cuando los unimos, aprendemos juntos y somos capaces de resolver cualquier desafío.
Por ello es importante que en tu equipo sigáis estos consejos:
- Todo lo que una persona sabe lo comparte con los demás.
- Colaboramos en las tareas para que el equipo funcione.
- Valoramos los superpoderes de cada persona.
- Respetamos lo que cada persona ofrece al equipo.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0