Diccionario
Adiestrar
Crea tu emblema numerorum
4.1 Descubre los números poligonales
Números poligonales
El primer adiestramiento en esta Academia es el de los números poligonales.
¿Te acuerdas cuando colocamos los monopatines para poder llegar al siguiente nivel?
Estaban colocados como una pirámide, con forma de triángulo.
No es la única forma de organizarlos.
Podíamos colocarlos como un cubo, con forma de cuadrado.
Esta idea se puede extender a diferentes formas geométricas.
Los matemáticos de la Antigüedad descubrieron que los números podían disponerse con ciertas formas cuando los representaban mediante piedras o semillas.
Descubrieron los llamados números poligonales
Poligonales
Un número poligonal es un número natural que puede recomponerse en un polígono regular. Los hay de distinto nombre:
- triangulares
- cuadrados
- pentagonales
- etc...
Triangulares
Los números triangulares son aquellos números que se pueden representar con puntos que formen un triángulo regular:
Cuadrados
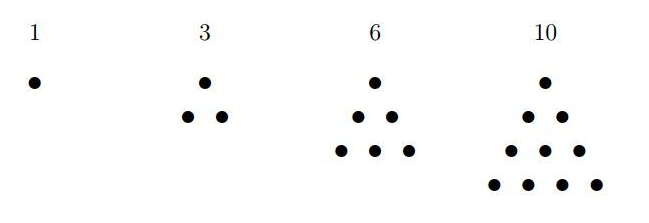
Los números cuadrangulares son aquellos números que se pueden representar con puntos que formen un cuadrado:
Pentagonales
Los números pentagonales son aquellos números que se pueden representar con puntos que formen un pentágono regular:
Lectura facilitada
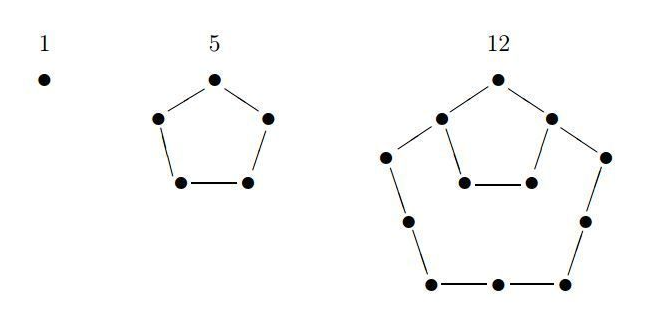
Ya estás en la Academia Numerorum.
El primer adiestramiento es el de los números poligonales.
¿Recuerdas como colocabas los monopatines para llegar al siguiente nivel?
Los monopatines estaban colocados como una pirámide o en forma de triángulo.
Hay muchas más formas de organizarlos.
Por ejemplo, como un cubo o forma de cuadrado.
Los matemáticos de la Antigüedad descubrieron los llamados números poligonales.
Números poligonales
Un número poligonal es un número natural que puede recomponerse en un polígono regular.
Los hay de distinto nombre:
- triangulares
- cuadrados
- pentagonales
- etc...
Números triangulares
Los números triangulares son aquellos números que se pueden representar con puntos que formen un triángulo regular:
https://www.geogebra.org/m/TQP3NTSF
Números cuadrados
Los números cuadrangulares son aquellos números que se pueden representar con puntos que formen un cuadrado:
https://www.geogebra.org/m/vwm5w5uf
Números pentagonales
Los números pentagonales son aquellos números que se pueden representar con puntos que formen un pentágono regular:
https://www.geogebra.org/m/hyZXm2FU
Otros números poligonales
Aquí tienes algunos números poligonales.
Se organizan según su tipo y su orden, como puedes ver en el siguiente cuadro:
Descubriendo a los números poligonales
Ahora vamos a realizar diferentes actividades, para que sepas identificar los distintos números poligonales.
Además podrás conseguir nuevas insignias para realizar tu emblema.
Opción A: Formando números poligonales
Botón de la Insignia de la Gema
Si has superado el reto, has conseguido la Insignia de la Gema. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción B: Fíjate y descubre a los números poligonales
Queremos saber si los número 26 y 18 son triangulares.
¿Cuál sería el siguiente triángulo?
¿Te acuerdas cómo construíamos los números triangulares?
Comenzábamos con un punto. El 1 es un número triangular
Luego añadíamos dos más para obtener el primer triángulo. El 3 es un número triangular.
Posteriormente hacían falta tres puntos más para formar otro triángulo más grande. El número 6 es un número triangular.
Finalmente poníamos cuatro más para obtener el último triángulo. El número 10 es un número triangular.
.
Pero este proceso no se acaba aquí, podemos seguir.
Obtenemos más número triangulares
Si queremos otro más, tendríamos que añadir cinco puntos más y el 15 sería un número triangular
Buscando la solución
Queremos saber si los números 26 y 28 eran números triangulares.
Tenemos que seguir el proceso hasta que lleguemos a ese número, en ese caso será un número triangular
o nos lo saltemos, y en ese caso no será un número triangular.
Para el siguiente triángulo tendríamos que añadir seis puntos, y tendríamos que el 21 es un número triangular:
todavía no hemos llegado ni al 26, ni al 28, por tanto hay que seguir el proceso.
Encontrando la solución
Para el siguiente triángulo tenemos que añadir siete nuevos puntos:
llegamos al número 28.
Por tanto el número 28 es un número triangular, pero el 26 no es un número triangular porque nos lo hemos saltado ya.
Ahora vas a tener que adivinar sí los números 32 y 36, son números cuadrados.
Recuerda cómo se construían los cuadrados:
y sigue la secuencia hasta que encuentres o te saltes al 32 y al 36.
Botón de la Insignia del Topacio
Si has superado el reto, has conseguido la Insignia del Topacio. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Botón de la Insignia del Zafiro
Si has superado el reto, has conseguido la Insignia del Zafiro. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción C: Identificando números poligonales
Tienes que responder si los siguientes números son poligonales
Retroalimentación
Verdadero
Si vas construyendo los números triangulares, el quinto es el 15
Retroalimentación
Falso
Retroalimentación
Verdadero
Botón de la Insignia del Diamante
Si has superado el reto, has conseguido la Insignia del Diamante. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción D: Descubre los números poligonales
Clasifica los números que aparecen en la tabla en triangulares, cuadrado y pentagonales. Ten en cuenta que pueden pertenece a varios tipos.
Contesta S o N en cada recuadro.
Botón de la Insignia de la Estrella
Si has superado el reto, has conseguido la Insignia de la Estrella. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Opción E: Crea números poligonales
Responde a las siguientes cuestiones
¿Son los números 6 y 10 triangulares?
¿Y el 16?
¿Es el 16 un número cuadrado?
¿Son los números 15 y 21 triangulares?
¿Y el 36?
¿Es el 36 un número cuadrado?
¿Puedes formular alguna hipótesis entre los números triangulares y los cuadrados?
Botón de la Insignia de la Estrella
Si has superado el reto, has conseguido la Insignia de la Estrella. Con ella en tu poder podrás usarla para construir vuestro Emblema Numerorum. No olvides incluirla en el cuaderno de bitácora.
Los números y la geometría están unidos
Los matemáticos antiguos ya se dieron cuenta que las propiedades de algunos números estaban relacionadas con las formas geométricas más simples.
En estas actividades habéis podido comprobarlo.
Esta relación se extiende a figuras mas complejas.
Si estás interesado puedes buscar información sobre los fractales.
Botón de la Insignias de los Números Poligonales
Podréis conseguir la maravillosa Insignia de los Números Poligonales para vuestro grupo cuando acabéis vuestro adiestramiento.
¿Tienes dudas?
¿Te has sentido seguro en esta actividad?
A veces cuando nos enfrentamos a una actividad nos pueden surgir dudas sobre si vamos a ser capaz de hacerla adecuadamente.
Pero estos miedos los podemos vencer. Para ello te voy a dar unos consejos:
1. Hay cosas que haces muy bien. Úsalas para hacer la actividad.
2. Hay cosas que te cuestan un poco hacerlas. Inténtalo y cree en ti mismo o en ti misma. Seguro que te sorprende lo que puedes conseguir.
3. Hay cosas que son muy difíciles. Fíjate en algún ejemplo, pregunta a tu compañero o compañera. Pide ayuda a tu profe.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0