Saltar la navegación

4.5. Funciones a trozos

Rectoparábolo dice...

Mi querida Afunción, has aprendido muchas funciones nuevas, pero aún no hemos terminado. ¿Sabías que podíamos combinar cualquiera de estas funciones? Esto nos va a servir para nuestro reto final

Vamos a aprender cómo combinar las funciones. ¡Son las funciones a trozos!

Lectura facilitada

Afunción ha aprendido muchas funciones nuevas.

¿Sabes que puedes combinar las funciones? 

Combinar las funciones te va a servir 

para resolver el reto final. 

Vas a aprender cómo combinar las funciones.

¡Son las funciones a trozos!

1. Troceamos funciones

En ocasiones nos encontramos gráficas en los que no aparece una única función. En este trabajo ya hemos visto algunas:

  • Recuerdas el Paseo al Mulhacén, trazaste el recorrido hasta el Mulhacén con varias rectas.
  • En el Basket de funciones utilizaste una recta y una parábola.

Como has observado ya has utilizado funciones a trozos. Ahora es el turno de conocerlas mejor.

Lectura facilitada

Hay gráficas en la que aparecen varias funciones. 

Fíjate en los ejemplos. 

  • Recuerda el Paseo al Mulhacén.
             Trazaste el recorrido hasta el Mulhacén con varias rectas. 
  • En el Basket de funciones utilizaste una recta y una parábola. 

Ya has utilizado funciones a trozos. 

Ahora es el turno de conocerlas mejor. 


Una función a trozos es aquella que está definida con diferentes expresiones análiticas (o gráficas) en diferentes intervalos del domino (o tramos).

La función se enumera de izquierda a derecha (orden creciente de valores de x) indicando a la expresión el intervalo en el qué está definida. Veamos un ejemplo.

f(x)= \left\{ \begin{array}{lcc} 5 & si & x \leq 2 \\ \\ x^2-6x+10 & si & 2 < x < 5 \\ \\ -x^2+10x-25 & si & x \geq 5 \end{array} \right.

La imagen muestra una función a trozos

Lectura facilitada

Una función a trozos es aquella qué está dividida con diferentes gráficas 

en diferentes tramos. 

La función se enumera de izquierda a derecha.

Orden creciente de valores de x.

Indica el intervalo en el que se define la función. 

Observa un ejemplo. 

f(x)= \left\{ \begin{array}{lcc} 5 & si & x \leq 2 \\ \\ x^2-6x+10 & si & 2 < x < 5 \\ \\ -x^2+10x-25 & si & x \geq 5 \end{array} \right.

La imagen muestra una función a trozos

La función será continua si las dos funciones se aproximan al mismo valor.

La función será discontinua si las funciones se aproximan a valores diferentes.

En el ejemplo anterior observamos los puntos de salto, cuando cambia de una función a otra:

  • Para x=2: la función es discontinua, ya que se observa un salto de 5 a 2, que son los valores que toman las ramas que se aproximan a 2 desde valores más pequeños y mayores, respectivamente.

  • Para x=5: tanto para valores menores que 5 como para mayores el valor de la función es 5. Por lo tanto la función es continua, en la gráfica no hay separación entre las dos ramas que se aproximan a 5.

Lectura facilitada

La función será continua cuando las dos funciones 

se acercan al mismo valor. 

La función será discontinúa cuando las dos funciones 

se acercan a valores diferentes. 

  • Para x=2. 

         La función vale 5 para valores menores que 2.

         La función vale 2 para valores mayores. 

         La función es discontinua. 

         La función toma valores diferentes. 

         Observa el salto que aparece en la gráfica. 

  • Para x=5.

         El valor de la función es 5 para valores mayores y menores que 5. 

         La función es continua.

         En la gráfica no hay separación entre las dos funciones. 

2. Valor absoluto

La función valor absoluto de f(x), se representa |f(x)|, es un caso particular de funciones a trozos.

  • Gráficamente consiste en convertir en positivos los valores negativos de la función, la gráfica es su simétrica respecto de eje x.
  • La expresión analítica es la de una función a trozos, donde se cambia de signo la función en el intervalo de valores de x en los que la función toma valores negativos.

Veamos un par de ejemplos.

Función lineal

f(x)= \left\{ \begin{array}{lcc} -(2x-4) & si & x < 2 \\ 2x-4 & si & x \geq 2 \end{array} \right.

La imagen muestra el valor absoluto de una recta

Parábola

f(x)= \left\{ \begin{array}{lcc} x^2-4 & si & x \leq -2 \\ \\ -(x^2-4) & si & -2 < x < 2 \\ \\ x^2-4 & si & x \geq 2 \end{array} \right.

La imagen muestra el valor absoluto de una parábola

Lectura facilitada

La función valor absoluto de \(f(x)\) se representa \(|f(x)|\). 

Consiste en convertir los valores negativos de la función 

en valores positivos.

La expresión analítica es la expresión de una función a trozos.

Se cambia de signo la función en el intervalo de valores de \(x\).

Se cambian a positivo los valores de \(x\) 

en los que la función toma valores negativos.

La función es positiva en todo su dominio.

La gráfica es su simétrica respecto de donde corta en el eje \(x\).

Observa los ejemplos. 

Función lineal

f(x)= \left\{ \begin{array}{lcc} -(2x-4) & si & x < 2 \\ 2x-4 & si & x \geq 2 \end{array} \right.

La imagen muestra el valor absoluto de una recta

La función f(x) está definida en dos trozos. 

  • En el primer trozo, la expresión de la función es \( -(2x-4)\) 

        cuando \(x\) toma valores más pequeños que 2.

        Cambiamos el signo de la función

        porque \(2x-4\) toma valores negativos 

        cuando \(x\) toma valores más pequeños que 2. 

  • En el segundo trozo, la expresión de la función es \(2x-4\) 

         cuando \(x\) toma valores más pequeños que 2. 

         No cambiamos el signo de la función

         porque \(2x-4\) es positivo

         cuando \(x\) toma valores más grandes que 2. 

Parábola

f(x)= \left\{ \begin{array}{lcc} x^2-4 & si & x \leq -2 \\ \\ -(x^2-4) & si & -2 < x < 2 \\ \\ x^2-4 & si & x \geq 2 \end{array} \right.

La imagen muestra el valor absoluto de una parábola

La función \(f(x)\) está definida en tres trozos.

  • En el primer trozo la expresión de la función es \(x^2- 4\).

         Cuando \(x\) toma valores más pequeños que -2.

         No cambiamos el signo

         porque \(x^2- 4\) da valores positivos.

  • En el segundo trozo la expresión de la función es \(- (x^2- 4)\).

         Cuando \(x\) toma valores que están entre -2 y 2

         Porque \(x^2- 4\) da valores negativos

         cuando \(x\) toma valores entre -2 y 2.

  • En el tercer trozo la expresión de la función es \(x^2- 4\). 

         Cuando \(x\) toma valores más grandes que 2

         No cambiamos el signo

         porque \(x^2- 4\) da valores positivos.

3. Vamos a trocear funciones

Afunción dice...

Creo que las funciones a trozos no son tan complicadas, además me serán muy útiles a la hora de diseñar el recorrido del Mathematical Sport Challenge.

Opción A. Manipulo el valor absoluto

Genera una recta.

Sitúa los tres puntos de la recta sobre valores negativos.

Sitúa los puntos asociados en el mismo valor pero en positivo.

Comprueba qué has construido correctamente la función valor absoluto.

https://www.geogebra.org/m/tuubx64y (Ventana nueva)

Mayte%20Siles,https%3A//www.geogebra.org/m/udmpnx58,Manupula.ValorAbsoluto,0,Autor%EDa

Ves, es muy fácil. Puedes repetir el ejercicio tantas veces como quieras hasta qué seas capaz de dominarlo.

Opción B. Cada oveja con su pareja

Opción C. Ya sé pintar

Representa graficamente las siguientes funciones valor absoluto, indicando su expresión analítica.

  1. \(y=|3-2x|\)

  2. \(y=|x+5|\)

  3. \(y=|x^2-4x|\)

  4. \(y=|x^2-3x-4|\)

Opción D. Maestro de funciones

Representa las siguientes funciones a trozos. En cada caso indica si la función es continua o no.

  1. f(x)= \left\{ \begin{array}{lcc} 0 & si & x \leq -1 \\ x+2 & si & -1 < x < 1 \\ 3x-2 & si & x \geq 1 \end{array} \right.

  2. f(x)= \left\{ \begin{array}{lcc} -1-x & si & x \leq -1 \\ 1-x+2 & si & -1 < x < 1 \\ x-1 & si & x \geq 1 \end{array} \right.

Opción E. Mix de funciones

Opción F. En el banco

Afunción ha recibido un adelanto de 1000€ para hacer el diseño de la pista. Aconsejada por Rectoparábolo ha acudido al banco y le han ofrecido un interés compuesto mensual del 1% durante los tres primeros meses. Pasado este tiempo pasará a recibir un interés simple del 1,25%. Afunción ha decidido dejar su dinero hasta que haya completado el diseño de la prueba y reciba todo lo acordado.

  1. Expresa de forma analítica (en meses) el interés generado por el adelanto recibido.
  2. Representa gráficamente la función del interés recibido.

Lumen dice... ¿No recuerdas bien el interés?, puedo ayudarte.

Hay dos tipos de interés.

El Interés simple no acumula los intereses al capital su expresión es: \(C_f=C_0 (1+\Large\frac{r}{100} \normalsize \ t)\)

El Interés compuesto acumula los intereses al capital, su expresión es: \(C_f=C_0 (1+\Large\frac{r}{100}\normalsize)^t\)

Donde: \(C_f\): es el capital final

\(C_0\): es el capital inicial

\(r\): es el interés

\(t\): es el tiempo

4. Diseño de una pista de SKATE

Escogiendo dos de los 4 tipos de funciones trabajadas anteriormente, seleccionad dos de ellas y tendréis que diseñar la pista de skate que queremos construir en las pistas de esquí. Como ya sabéis cómo son, solo tendréis que darle forma a las paredes de la pista. De las tres opciones pulsa en "Patio" y ahí tendrás los "ladrillos" ladrillo para construir la pista. Tenéis que pulsar el círculo rojo del centro y arrastrarlo a la pista. Podréis estirarlo por los bordes y ponerlo como quieras. Luego coge otro y haz lo mismo. Os daréis cuenta que si aproximas el círculo rojo derecho del primero con el izquierdo del segundo se unirán. Así que si repetís este proceso muchas veces podréis ir construyendo poco a poco vuestra pista de Skate (como la vista en la sección "De camino"). Cuidado que no la tenéis que unir como queráis, tendréis que darle forma (Podéis ayudaros mostrando la cuadrícula) y tanto la pared izquierda como la derecha, tienen que ser dos de las funciones trabajadas en la parte I del super reto. 

Cuando terminéis de diseñarla, cogéis a nuestro patinador y lo ponéis en la pista. Podéis modificar su masa y la fricción entre la pista y el monopatín. También podréis verlo más lento o más rápido. Si os equivocáis en unos ladrillos y queréis quitarlos, pulsad en un círculo rojo y os saldrá unas tijeras y una x. Las tijeras sirven para separar los ladrillos y la x para quitar el punto rojo. 

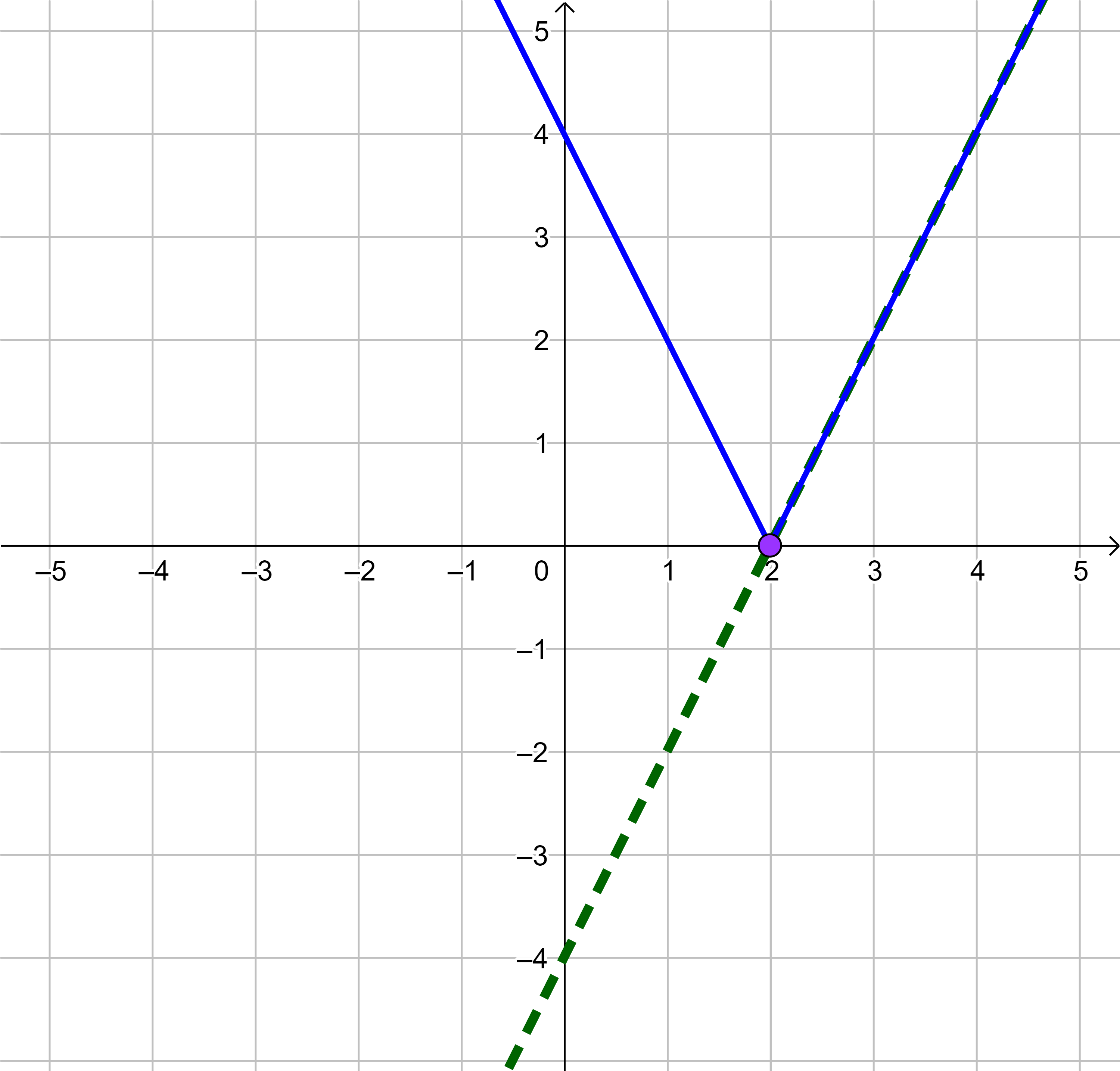
Una vez que ya lo hayáis construido, haced una captura de pantalla y cargad esa imagen en Geogebra, tal y como hicísteis en la parte "3. Nos pertrechamos" y comprobad cual es la ecuación de cada una de las dos paredes diseñadas. 

  • Enviad a vuestro profesor o profesora la imagen de vuestra pista de skate con las ecuaciones de las funciones (las paredes de la pista de skate)

Ampliación funciones a trozos

  • Podemos utilizar 3 ó 4 funciones para construir la pista si quieres. 
  • La pared de la izquierda tiene que ser decreciente y la derecha creciente, reflexiona sobre cómo influye en nuestras paredes una cualidad de las funciones que se llama concavidad y convexidad. 

Clavis dice... ¿Te has sentido confiado o confiada en la realización de estas actividades?

Cuando tenemos que hacer alguna actividad, como por ejemplo la actividad de “Manipulo el valor absoluto”,  podemos tener dudas sobre si seremos capaces de hacerlo.

Para poder vencer a estos miedos en las nuevas actividades que tengas que hacer sigue estos consejos:

  1. Hay cosas que haces muy bien. Úsalas para hacer la actividad.
  2. Hay cosas que te cuestan un poco hacerlas. Inténtalo y cree en ti mismo o en ti misma . Seguro que te sorprende lo que puedes conseguir.
  3. Hay cosas que son muy difíciles. Fíjate en algún ejemplo, pregunta a tu compañero o compañera. Pide ayuda a tu profe.

5. Reviso lo que aprendo

Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. 

Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido). 

Recuerda:

• Pregunta a tu profesor o profesora si la rellenas en papel o en el ordenador.

• Si la rellenas en el ordenador, ¡no te olvides de guardarla en tu ordenador cuando la termines!

¡Ánimo, que lo harás genial!