Diccionario
Arqueología

Astronomía

Bisectriz
Decibelios

Umbral


Bueno, bueno Afunción, vamos a estudiar los logaritmos. Para ello, te propongo salir esta noche por Pradollano. ¿Te apetecería cenar en un buen restaurante, después tomar unos refrescos en un pub y para finalizar, ir a bailar a la discoteca? Será una buena forma de explicarte esta nueva función.
La respuesta afirmativa de Afunción no se hizo esperar, le gustaba salir y, además, estaba intrigada sobre lo que le iba a enseñar Rectoparábolo y cómo lo haría.
Lectura facilitada
Afunción vas a estudiar los logaritmos.
Rectoparábolo le propone a Afunción salir por Pradollano.
- Cenar en un restaurante.
- Tomar algún refresco en un pub.
- Bailar en una discoteca.
Kardia dice... ¿Te has preguntado cómo se mide el sonido?

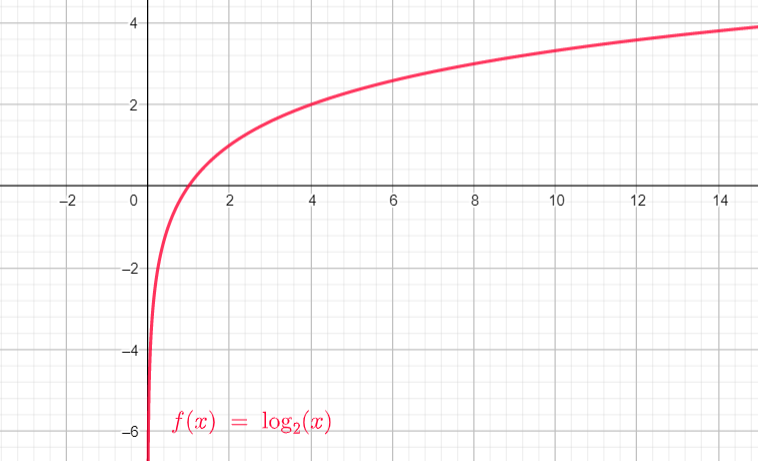
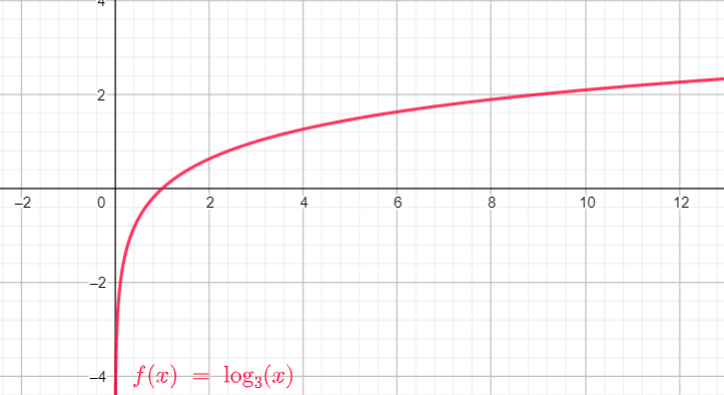
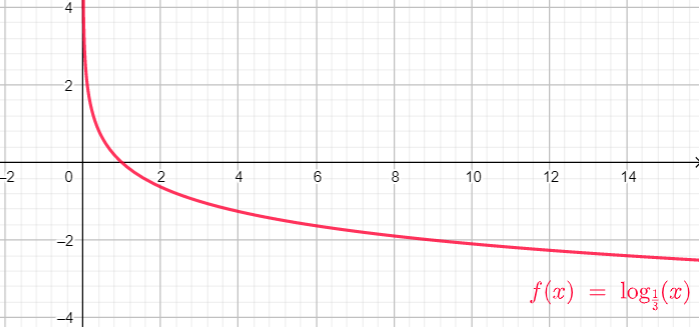
Recuerda que cuando la base del logaritmo es 10 no se indica

Unidad que se utiliza para medir la intensidad del sonido.
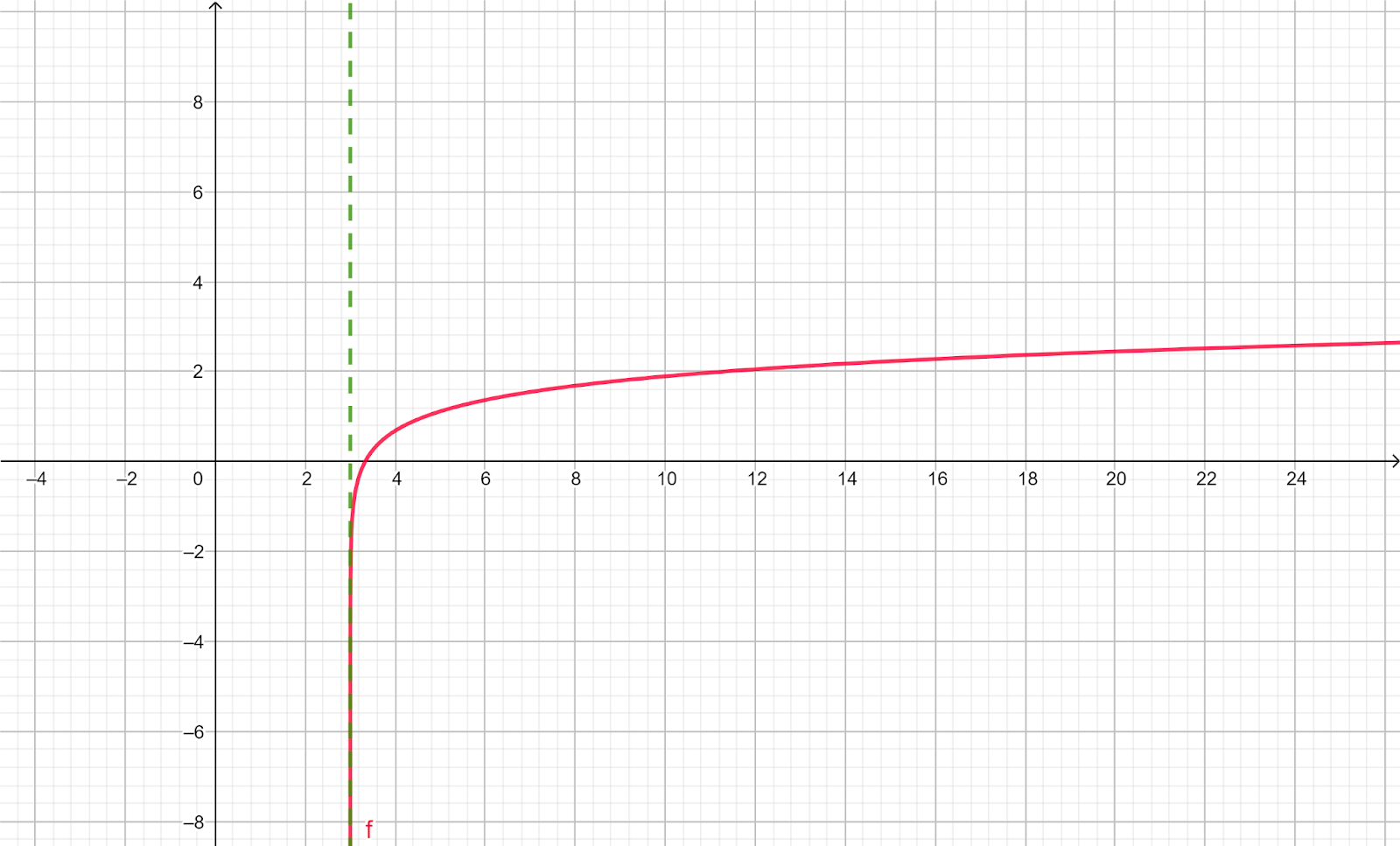
EjemploEn el restaurante se registraron 60 decibelios.

Intensidad mínima de un estímulo que despierta la sensación de dolor.
EjemploEl oído humano entra en el umbral del dolor a partir de 120 decibelios.
En el Sistema Internacional la unidad que se utiliza para medir la intensidad del sonido son los \(watios/m^2\)
Lectura facilitada

El nivel mínimo de un sonido para percibirlo es de \( 10^{-12}\ watios/m^2\).
La intensidad del sonido se mide con los \(watios/m^2\).
Los \(watios/m^2\) es una unidad del sistema internacional.
Para medir la intensidad de los sonidos se utilizan los belios y decibelios.
Esta unidad de medida se llama así en honor a Alexander Graham Bell.
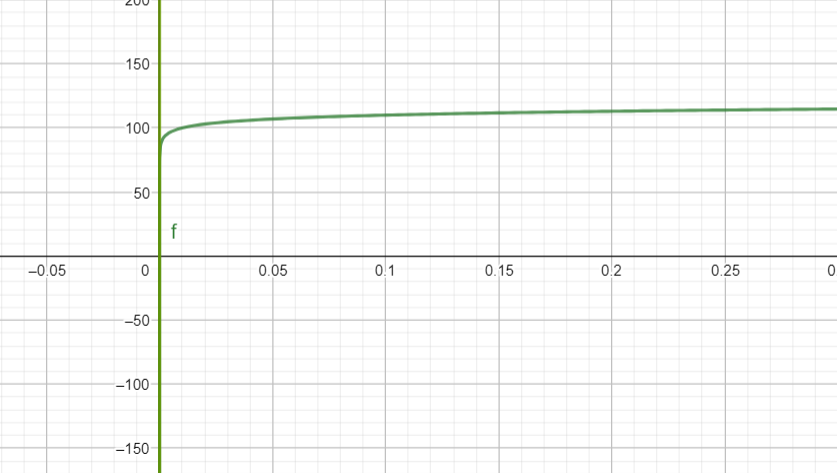
Esta escala se basa en la función logarítmica en base 10
para medir magnitudes muy grandes.
- Sin considerar el logaritmo.
- La \(x\) varía entre \(10^{-12}\) hasta 1.
- Al considerar el decibelio.
- El decibelio es \(10\cdot \log(10^{12}\cdot x)\).
- Varía de 0 a 120 decibelios.
- 120 decibelios es el umbral del dolor.
 Definición
Definición
Unidad que se utiliza para medir la intensidad del sonido.
EjemploEn el restaurante se registraron 60 decibelios.
 Definición
Definición
Intensidad mínima de un estímulo que despierta la sensación de dolor.
EjemploEl oído humano entra en el umbral del dolor a partir de 120 decibelios.