Diccionario
Saciados
Vamos al mercado
4.5. Repartiendo ingredientes
Multiplicación y división de fracciones
¿Recuerdas que en el apartado anterior calculábamos la cantidad de ingredientes que correspondían a cada uno?
Pues ahora vamos a profundizar con la preparación de una refrescante limonada.
Tenemos seis botellas de limonada. Cada una de ellas tiene una capacidad de 3/4 de litro.
Hemos comprado vasos de 2/5 de litro.
Queremos averiguar:
- ¿Cuánta limonada tenemos en total?
- ¿Cuántos vasos podemos llenar con una sola botella?
- Si repartimos la bebida entre todos, ¿cuánta nos corresponde a cada uno?
Para realizar estos cálculos utilizaremos la multiplicación y división de fracciones.
Multiplicar dos fracciones
Para multiplicar dos fracciones se multiplicarán los numeradores por un lado y los denominadores por otro, como en el ejemplo:
\[ \dfrac 2 3 \cdot \frac 5 7 = \frac {2·5} {3·7} = \frac {10} {21} \]
La regla de los signos se mantiene en la multiplicación de fracciones, como en los ejemplos:
\[ - \dfrac 1 2 \cdot \frac 3 4 = - \frac {1·3} {2·4} = - \frac {1} {8} \]
\[ - \dfrac 2 3 \cdot - \frac 5 7 = \frac {2·5} {3·7} = \frac {10} {21} \]
Multiplicar una fracción por un número
Para multiplicar una fracción por un número, lo consideraremos como una fracción con denominador 1, como en el ejemplo:
\[ \dfrac 4 5 \cdot 3 = \dfrac 4 5 \cdot \frac 3 1 = \frac {4·3} {5·1} = \frac {12} {5} \]
La regla de los signos se mantiene en la multiplicación de una fracción por un número.
Dividir dos fracciones
Para dividir fracciones se multiplicarán las fracciones en cruz como en el ejemplo:
\[ \dfrac 2 7 : \frac 3 4 = \frac {2·4} {7·3} = \frac {8} {21} \]
Es decir, se multiplica el numerador de la primera fracción por el denominador de la segunda y el denominador de la primera fracción por el numerador de la segunda fracción.
La regla de los signos se mantiene en la división de fracciones, como en los ejemplos:
\[ \dfrac 2 7 : - \frac 1 5 = - \frac {2·5} {7·1} = - \frac {10} {7} \]
Dividir una fracción por un número
En este caso se vuelve a considerar el número como una fracción con denominador 1, como en el ejemplo:
\[ \dfrac 4 5 : 3 = \dfrac 4 5 : \frac 3 1 = \frac {4·1} {5·3} = \frac {4} {15} \]
La regla de los signos se mantiene en la división de una fracción por un número, como en el ejemplo:
\[ -3 : \dfrac 3 4 = \dfrac {-3} 1 : \dfrac 3 4 = - \dfrac {3·4} {1·3} = - \dfrac {12} {3} = -4\]
A partir de aquí ya solo nos queda practicar estas operaciones, ¿te atreves?
Lectura facilitada
En el apartado anterior has visto cómo calcular
la cantidad de ingredientes que corresponde a cada persona.
Ahora vas a aprender con otra receta.
La receta de la limonada.
Tienes 6 botellas de limonada.
Cada una de ellas tiene una capacidad de ¾ de litro.
Has comprado vasos de 2/5 litros.
Tienes que calcular:
¿Cuánta limonada tienes en total?
¿Cuántos vasos puedes llenar con una sola botella?
Si repartes la bebida entre todos, ¿cuánta corresponde a cada persona?
Para realizar estos cálculos utilizaremos la multiplicación y división de fracciones.
Multiplicar dos fracciones
Para multiplicar dos fracciones
1º Multiplicas los numeradores
2º Multiplicas los denominadores.
Mira el ejemplo:
\[ \dfrac 2 3 \cdot \frac 5 7 = \frac {2·5} {3·7} = \frac {10} {21} \]
¡Importante!
La regla de los signos tienes que tenerla en cuenta en la multiplicación de fracciones.
¿Recuerdas?
+ x + = +
+ x - = -
- x + = -
- x - = +
Fíjate en los ejemplos:
\[ - \dfrac 1 2 \cdot \frac 3 4 = - \frac {1·3} {2·4} = - \frac {1} {8} \]
\[ - \dfrac 2 3 \cdot - \frac 5 7 = \frac {2·5} {3·7} = \frac {10} {21} \]
Multiplicar una fracción por un número
Cuando tengas que multiplicar una fracción por un número
tenemos que imaginar que el número que va a multiplicar a la fracción
tiene como denominador el número 1.
Luego multiplicas
numerador por numerador
y denominador por denominador.
Observa el ejemplo:
\[ \dfrac 4 5 \cdot 3 = \dfrac 4 5 \cdot \frac 3 1 = \frac {4·3} {5·1} = \frac {12} {5} \]
¡Importante!
La regla de los signos tienes que tenerla en cuenta en la multiplicación de fracciones.
¿Recuerdas?
+ x + = +
+ x - = -
- x + = -
- x - = +
Dividir dos fracciones
Cuando tengas que dividir fracciones
tienes que multiplicar las fracciones en cruz.
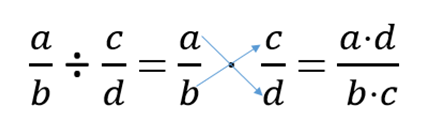
Fíjate en el ejemplo:
\[ \dfrac 2 7 : \frac 3 4 = \frac {2·4} {7·3} = \frac {8} {21} \]
1º Se multiplica el numerador de la primera fracción por el denominador de la segunda
2ºSe multiplica el denominador de la primera fracción por el numerador de la segunda fracción.
¡Importante!
La regla de los signos tienes que tenerla en cuenta en la multiplicación de fracciones.
¿Recuerdas?
+ x + = +
+ x - = -
- x + = -
- x - = +
Mira el ejemplo:
\[ \dfrac 2 7 : - \frac 1 5 = - \frac {2·5} {7·1} = - \frac {10} {7} \]
Dividir una fracción por un número
Para dividir una fracción por un número
tenemos que imaginar
que el número tiene denominador 1.
Mira el ejemplo:
\[ \dfrac 4 5 : 3 = \dfrac 4 5 : \frac 3 1 = \frac {4·1} {5·3} = \frac {4} {15} \]
¡Importante!
La regla de los signos tienes que tenerla en cuenta en la multiplicación de fracciones.
¿Recuerdas?
+ x + = +
+ x - = -
- x + = -
- x - = +
Fíjate en el ejemplo:
\[ -3 : \dfrac 3 4 = \dfrac {-3} 1 : \dfrac 3 4 = - \dfrac {3·4} {1·3} = - \dfrac {12} {3} = -4\]
Ahora tienes que practicar
¿Te atreves?
Multiplicación de fracciones
Hemos comenzado y la fiesta y ya hemos probado algunos de los platos y bebidas que hay en las mesas.
En las siguientes actividades vas a poner en práctica la multiplicación de fracciones.
Te animamos a realizar cuantas más, mejor.
Opción A. Demuestra lo que sabes
Responde a las siguientes preguntas para comprobar que has entendido la explicación.
Retroalimentación
Verdadero
Para multiplicar fracciones realizamos la siguiente operación:
\[ \dfrac 2 3 · \dfrac 7 4 = \dfrac {2·7} {3·4} = \dfrac{14}{12} \]
Retroalimentación
Falso
La operación no se realiza en ese orden.
Continuando con el ejemplo anterior, si tenemos seis botellas de 3/4 de litro, se calcula:
\[ \dfrac 3 4 · 6 = \dfrac {3·6} 4 = \dfrac {18} 4 \]
Opción B. Comprueba con papel la multiplicación de fracciones.
Doblando papel vamos a demostrar que:
\[ \dfrac 1 2 \cdot \dfrac 1 2 = \dfrac 1 4 \]
Un caso más sencillo: contando baldosas
Imagina que tienes un suelo rectangular y quieres contar cuántas baldosas tiene.
Lo más sencillo es contar las baldosas que hay a cada lado y, a continuación, multiplicarlas.
Para contar las baldosas del siguiente ejemplo:
4 · 6 = 24 baldosas en total
Vamos a usar un ejemplo similar a éste pero con fracciones para demostrar la multiplicación de fracciones.
Para demostrarlo, necesitamos representar estas fracciones en los lados del papel, es decir, representar la fracción \( \frac 1 2 \) en uno de los lados y la fracción \( \frac 1 2 \) en otro de los lados.
El resultado final será el resultado de multiplicar ambas fracciones.
Seguiremos los siguientes pasos:
Coge un trozo de papel cuadrado o rectangular
Queremos representar la fracción \( \frac 1 2 \) en uno de los lados del papel
Dóblalo por la mitad en uno de los lados.
En el ejemplo hemos dividido el papel en horizontal.
Tenemos dividido el cuadrado en dos partes iguales.
Colorea una de las mitades
De esta manera representaremos la fracción \( \frac 1 2 \) en uno de los lados porque el cuadrado está dividido en dos partes iguales y hemos coloreado una de ellas.
Ahora representamos la otra fracción \( \frac 1 2 \) en el otro lado.
Dóblalo por la mitad por el otro lado (en el ejemplo lo hemos doblado en vertical)
Colorea una de las mitades dobladas
En el ejemplo hemos coloreado en amarillo la primera parte vertical:
De esta manera verás que ha quedado doblado el papel en cuatro trozos iguales y que has coloreado dos veces uno de los trozos.
Ése trozo representa \( \frac 1 4 \)
¡Es tu turno!
Demuestra que \[ \dfrac 1 2 \cdot \dfrac 2 3 = \dfrac 2 6 = \dfrac 1 3 \]
Opción C. Busca el error en la multiplicación de fracciones
Solución
Solución
Opción D. ¿Cuánta comida ha sobrado?
En la explicación anterior aparece la multiplicación y división de fracciones.
En ese ejemplo se aplican estas operaciones para calcular la cantidad de bebida.
Ahora queremos aplicar estos conocimientos para saber cuánta comida ha sobrado.
Los siguientes botones pueden ayudarte en esta tarea.
Si no necesitas ayuda, puedes pasar directamente a calcular la cantidad de comida que sobra.
Un ejemplo: calculamos la cantidad total de bebida de la fiesta
Tal y como se indica en la receta, tenemos seis botellas de 3/4 litro.
Para calcular cuánta bebida tenemos en total, tendremos que multiplicar ambas cantidades:
\[ \dfrac 3 4 · 6 = \dfrac 3 4 · \dfrac 6 1 = \dfrac {3·6} 4 = \dfrac {18} 4 \]
¿Tienes dudas? Quizás con el siguiente ejemplo puedas entenderlo.
Tenemos 4 botellas de 2 litros cada.
¿Qué operación necesitas para calcular la cantidad total de limonada?
Usaremos la multiplicación: 4 botellas · 2 litros cada botella = 8 litros de limonada
Ha llegado tu turno.
Tal y como vimos, los ingredientes que añadiremos a la pizza son los siguientes:
- 150 gramos de salsa de tomate
- 60 gramos de cada tipo de queso: mozzarella, gorgonzola, parmesano y ricotta
- 5 gramos de orégano (opcional)
Hemos dividido la pizza en ocho partes.
Una vez todos estamos saciados, hemos comprobado que han sobrado dos trozos de pizza.
¿Podrías calcular cuánto tomate ha sobrado?
¿Podrías calcular cuánto queso ha sobrado?
Opción E. ¿Qué más puedes aportar?
A la vista de todo lo anterior, ¿serías capaz de diseñar un ejercicio en el que intervenga la multiplicación de fracciones?
Recuerda que no solo usamos las fracciones en la cocina sino en muchas otras situaciones.
División de fracciones
Hemos comenzado y la fiesta y ya hemos probado algunos de los platos y bebidas que hay en las mesas.
En las siguientes actividades vas a poner en práctica la división de fracciones.
Te animamos a realizar cuantas más, mejor.
Opción A. Demuestra lo que sabes
Retroalimentación
Falso
Solo es necesario que los denominadores sean iguales al sumar o restar fracciones.
Para dividir fracciones se realiza la siguiente operación:
\[ \dfrac 2 7 : \frac 3 4 = \frac {2·4} {7·3} = \frac {8} {21} \]
Retroalimentación
Verdadero
El siguiente ejemplo recuerda cómo se realizan las divisiones de fracciones:
\[ \dfrac 2 7 : \frac 3 4 = \frac {2·4} {7·3} = \frac {8} {21} \]
Opción B. Busca el error en la división de fracciones.
Solución
Solución
Opción C. ¿Cuántas pizzas podemos preparar?
Aplica tus conocimientos para preparar tu propia fiesta.
Has ido al mercado a realizar la compra y, al llegar a casa has colocado todos los ingredientes en la encimera de tu cocina.
Para comprobar que no te falta nada, vuelves a repasar lo que has comprado:
- 1/2 kg de salsa de tomate
- 1/4 kg de cada queso: mozzarella, gorgonzola, parmesano y ricotta
- 1 bote de 20 gramos de orégano
Quieres usar la receta de pizza para el mayor número de personas.
Recuerda los ingredientes de la pizza
Los ingredientes de la pizza son:
- 150 gramos de salsa de tomate
- 60 gramos de cada tipo de queso: mozzarella, gorgonzola, parmesano y ricotta
- 5 gramos de orégano (opcional)
¿Podrías calcular cuántas pizzas podrías rellenar con esa salsa de tomate?
¿Podrías calcular cuántas pizzas podrías rellenar con esa cantidad de queso?
¿Podrías calcular cuántas pizzas podrías rellenar con esa cantidad de orégano?
Sugerencia para calcular la cantidad total de receta
A la vista de los cálculos que has realizado, debes tener en cuenta que podrás elaborar la pizza si tienes todos los ingredientes para rellenarla.
Así, si por ejemplo tienes salsa de tomate para rellenar 6 pizzas pero solo tienes queso para 4 pizzas, solo podrás hacer 4 pizzas y reservar el tomate sobrante para otra elaboración.
A la vista de los resultados, ¿cuántas pizzas vas a poder preparar?
Opción D. ¿Qué más puedes aportar?
A la vista de todo lo anterior, ¿serías capaz de diseñar un ejercicio en el que intervenga la división de fracciones?
Recuerda que no solo usamos las fracciones en la cocina sino en muchas otras situaciones.
Reviso lo aprendido
Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido)
Recuerda:
• Pregunta a tu profesor o profesora si la rellenarás en papel o en el ordenador.
• Si la rellenas en el ordenador, ¡no te olvides de guardarla en tu ordenador cuando la termines!
¡Ánimo, que lo harás genial!
Es importante ajustar los ingredientes para que no sobre comida
Como has podido comprobar, usamos la multiplicación y división de fracciones en muchas ocasiones de la vida cotidiana:
- en recetas de cocina
- en repartos de gastos
- ...
Seguro que eres capaz de encontrar más situaciones en las que puedas aplicar la multiplicación y división de fracciones.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0