Diccionario
Superficie
Definición: Límite o término de un cuerpo , que lo separa y distingue de lo que no es él.
Ejemplo: En clase hemos calculado la superficie del patio.
¡Un patio del colegio más divertido!
4.3. Área del círculo: el número PI (𝝅)
En este apartado vamos a conocer qué ocurre cuando tenemos superficies en forma circular. Al no tener lados, el círculo aplica un número muy conocido en matemáticas: el número PI. Se usa una letra del alfabeto griego para representarlo: 𝝅. Aquí podrás conocerlo. Te hará falta conocerlo si alguno de tus juegos tienen forma de círculo o semicírculo. ¡Ánimo! ¡Seguro que te irá bien!
Definición: Límite o término de un cuerpo , que lo separa y distingue de lo que no es él.
Ejemplo: En clase hemos calculado la superficie del patio.
Lectura facilitada
En este apartado
vas a conocer
qué ocurre
cuando tenemos superficies
en forma circular.
Al no tener lados
el círculo aplica un número
muy conocido en matemáticas:
- el número PI
se usa una letra del alfabeto griego
para representarlo 𝝅
Aquí lo conocerás
Te hará falta
si alguno de tus juegos
tienen forma de:
- círculo
- semicírculo.
Seguro que lo vas a hacer genial
1. ¿Qué es?
Definición
¿Sabes cuántas veces cabe el diámetro de una circunferencia en su perímetro?
Usa esta presentación para entenderlo. Puedes cambiar el tamaño de la circunferencia y hacerla más grande o más pequeña.
Demostración
Fórmula
Como has podido comprobar, el diámetro de cualquier circunferencia siempre cabe en ella tres veces y un poquito. Esa relación, que siempre es la misma, es un número con infinitos decimales y se llama π (PI).
π = 3,1415926535…. pero para poder realizar nuestros cálculos nos quedaremos con dos decimales. Para las actividades que proponemos π= 3,14.
Lectura facilitada
Si quieres saber
cuantas veces
cabe el diámetro
de una circunferencia
en su perímetro,
con esta presentación
tú podrás entenderlo.
Puedes cambiar el tamaño
de la circunferencia
y así hacerla:
más grande
más pequeña
Como has podido comprobar
el diámetro
de cualquier circunferencia
siempre cabe en ella
tres veces y un poquito.
Esta relación
es un número
con infinitos decimales
se llama π (PI).
π = 3,1415926535
pero para poder realizar cálculos
nos quedaremos
con dos decimales.
para las actividades
que proponemos
π= 3,14.
Audio
2. Longitud de la circunferencia y área del círculo
Longitud de la circunferencia
El número π nos ayuda a calcular la longitud de una circunferencia. Si conocemos la medida del diámetro, únicamente tendremos que multiplicarlo por π porque sabemos que el diámetro está π veces en la circunferencia.
Si lo que conocemos es la medida del radio, primero debemos multiplicarlo por dos para conocer la longitud del diámetro.
| Longitud de la circunferencia = π x diámetro = π x D |
Área del circulo
Si pudiéramos cortar por un radio del círculo y abrirlo desde su centro, podríamos formar un triángulo. La base de ese triángulo corresponde con la longitud de la circunferencia y la altura con la longitud del radio, y solo faltaría dividirlo entre 2.
Presentación del circulo
Para que lo veas más claro, observa la siguiente presentación.
Gráfico del circulo
| Área del círculo = π x r² |
3. ¡Te toca a ti!
A continuación te presento varios ejercicios. Puedes hacer todos los que quieras. Son actividades sobre el gasto calórico y te servirán para conseguir el reto final con tus compañeros/as.
¡Ánimo, seguro que lo haces genial!
Opción A: ¿Conozco la circunferencia?
Organiza la información del esquema recordando lo que hemos aprendido anteriormente.
Opción B: El número π
Elige la opción correcta.
Opción C: Redondo, redondo
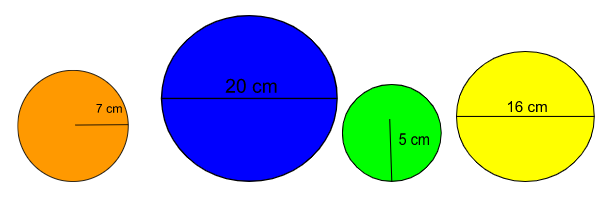
Copia estos círculos en tu cuaderno. Calcula la longitud de cada circunferencia y el área de cada círculo. Expresa las medidas en metros
Opción D: Buscador de círculos
Busca tres objetos que sean círculos de diferentes tamaños -a ser posible grandes-.
Realiza en tu cuaderno, las siguientes acciones con cada objeto.
- Mide su contorno, para ello puedes usar , una cuerda , un hilo….que colocarás sobre el instrumento de medida.
- Mide el diámetro de la circunferencia que forma en círculo.
- Pinta un círculo en tu cuaderno, escribe las medidas que has obtenido, a escala.
- Divide la medida del contorno entre la medida del diámetro.
- Piensa en el resultado que te han dado las divisiones.
- Calcula la longitud y el área de cada una de las circunferencias que forman los objetos.
- Añade un dibujo y las fórmulas al esquema realizado anteriormente.
Opción E: Mi video tutorial
Haz un video tutorial para tus compañeros y compañeras, explicando cómo se calcula el área del círculo. Para ello ,explica la relación que hay entre el área del triángulo y el área del círculo; tal y como has aprendido en este apartado
Puedes ayudarte de estas guías para crear el video tutorial:
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0