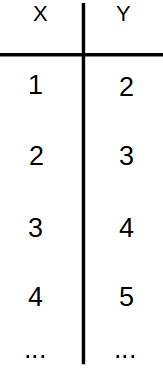Saltar la navegación

Créditos

1. Autoría

Imagen del Proyecto REA Andalucía

Título ¿Crees que está relacionado?
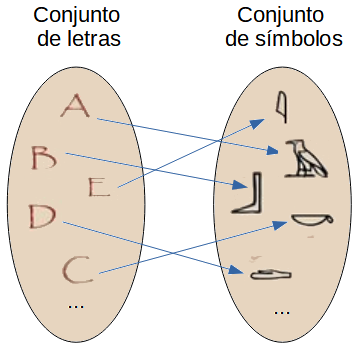
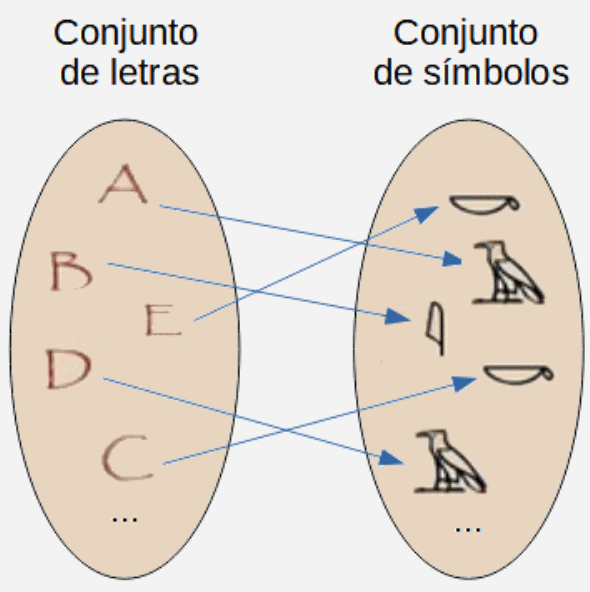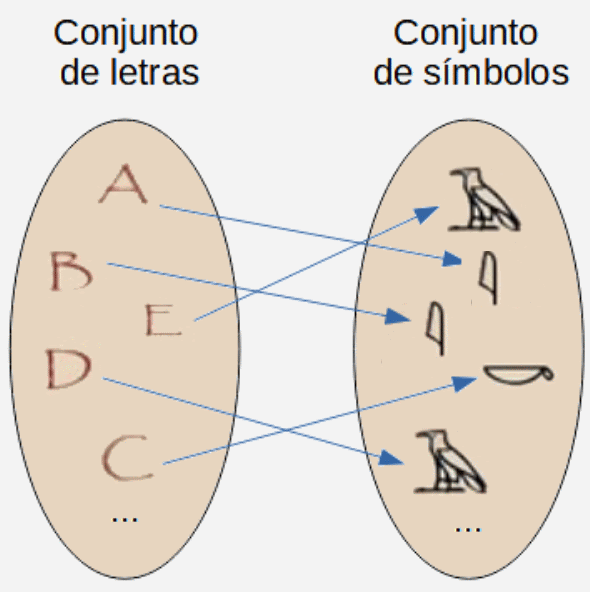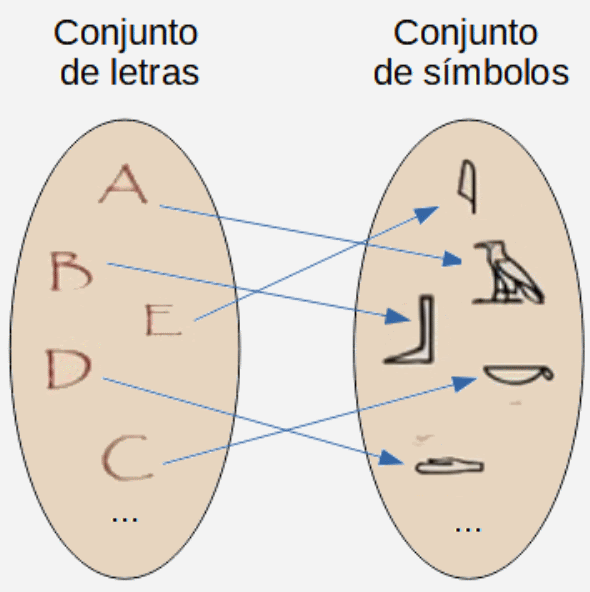
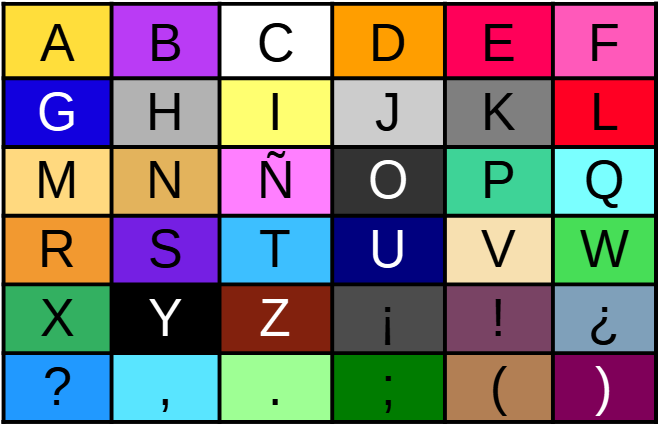
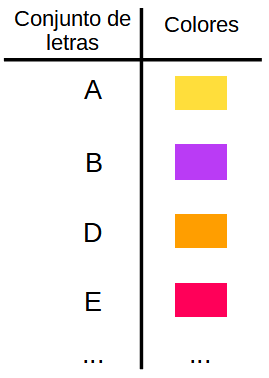
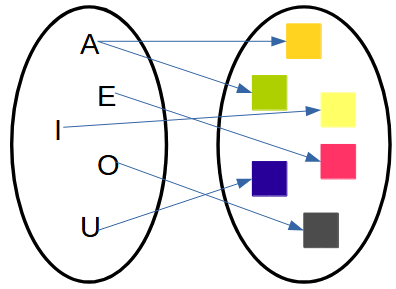
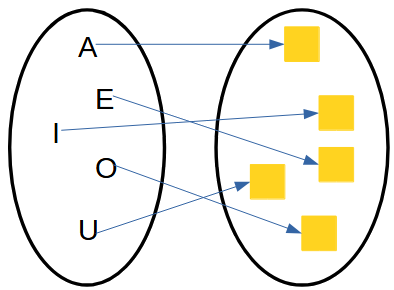
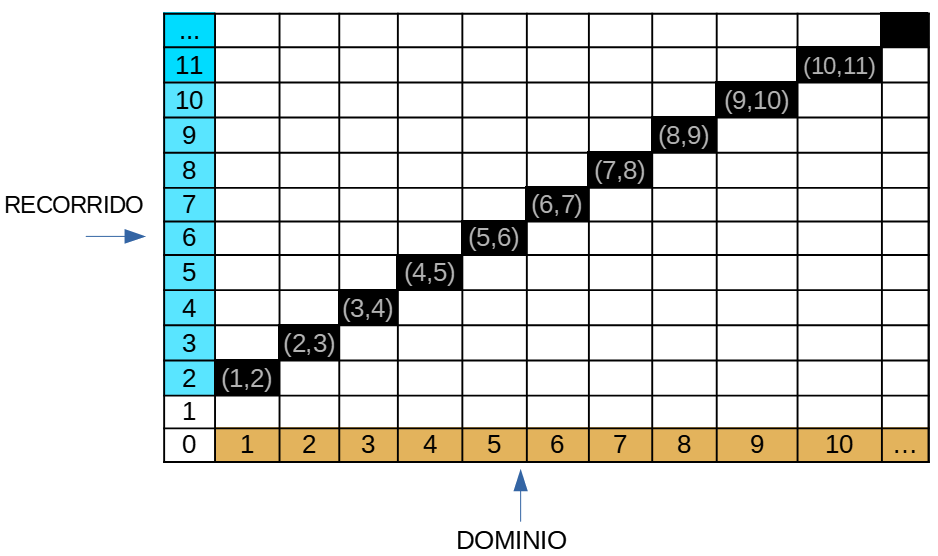
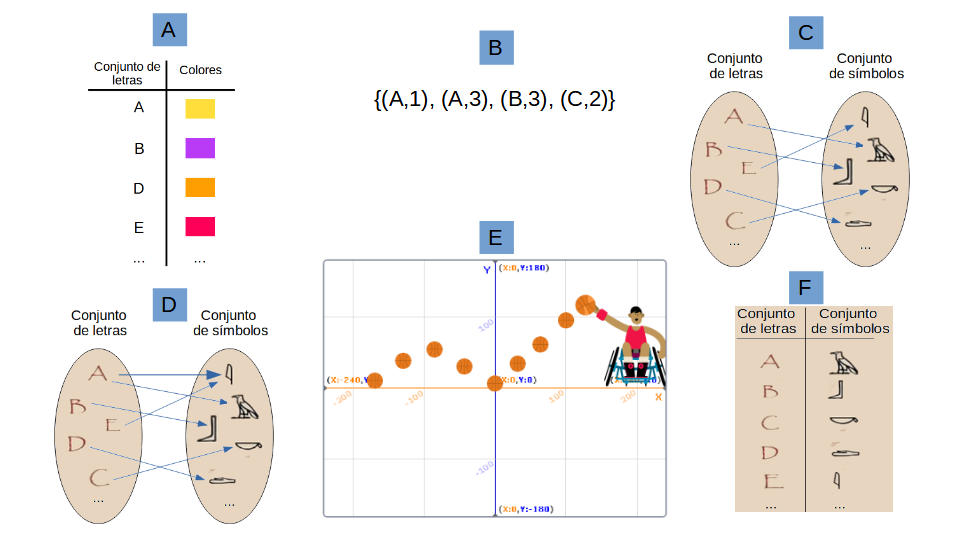
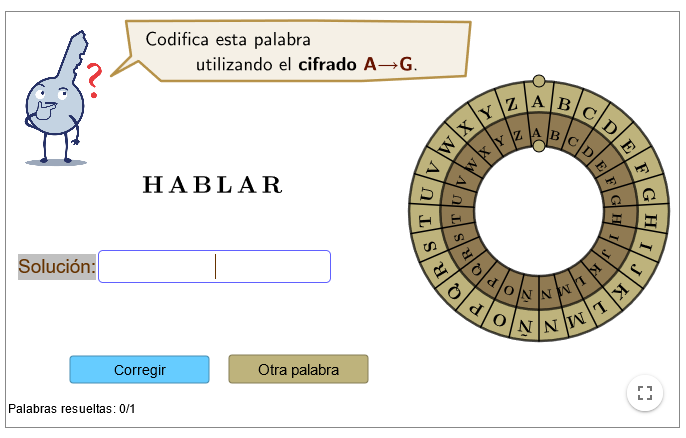
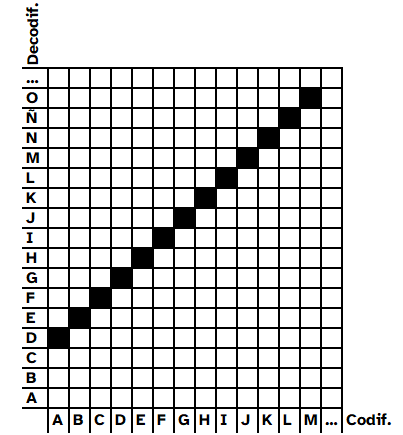
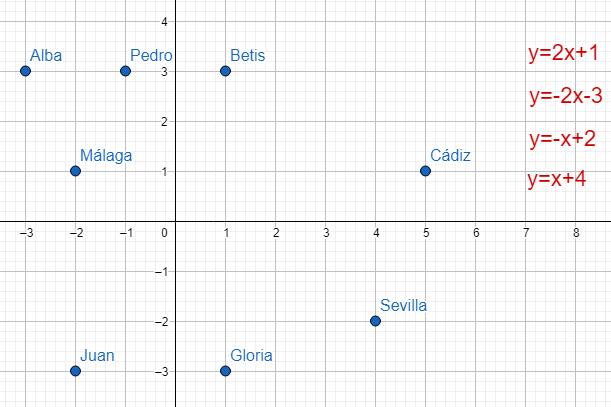
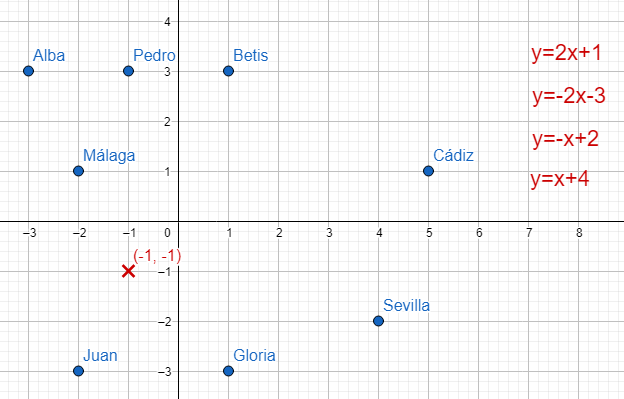
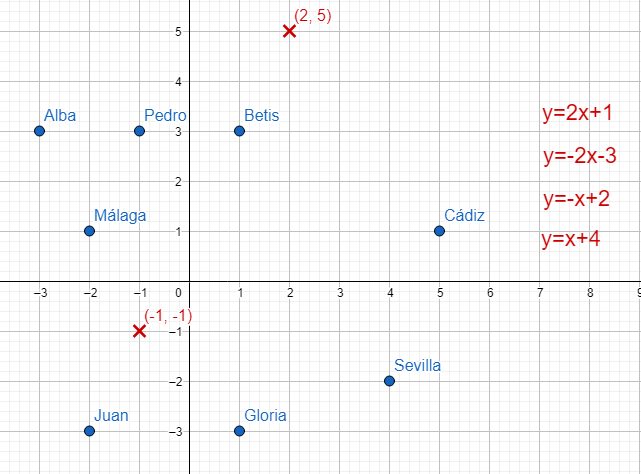
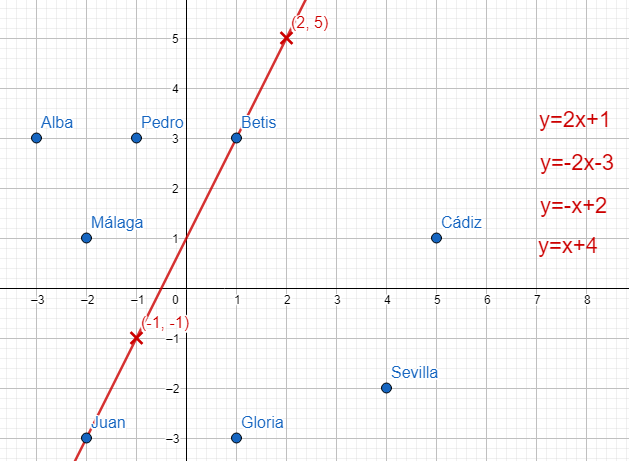
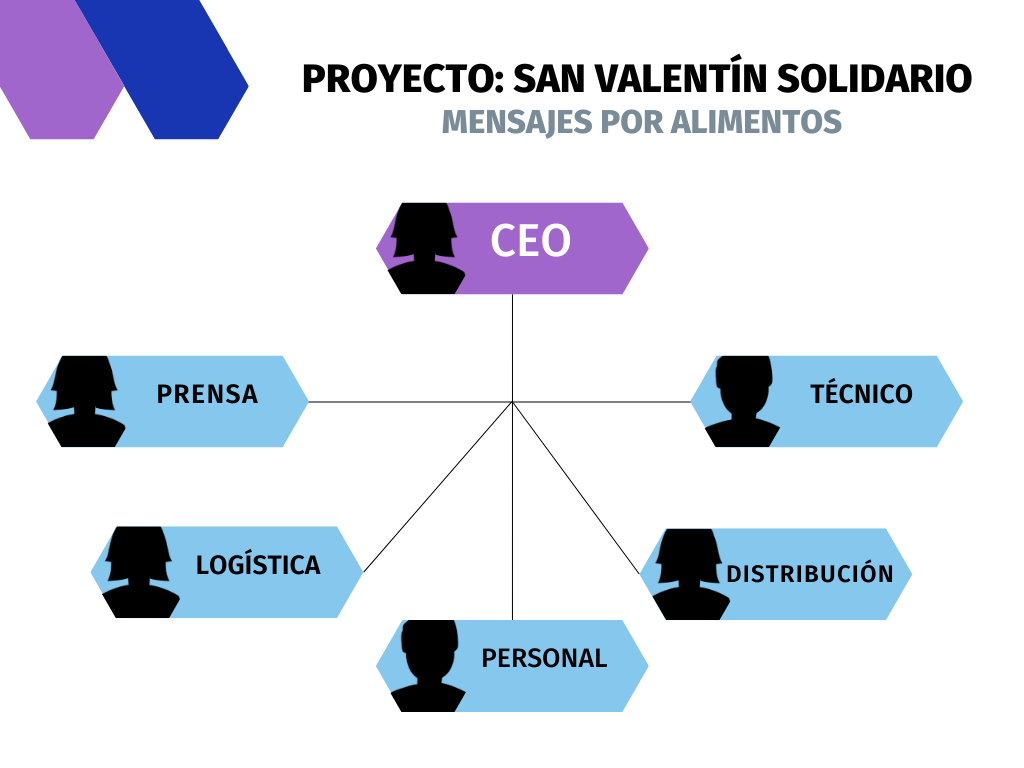
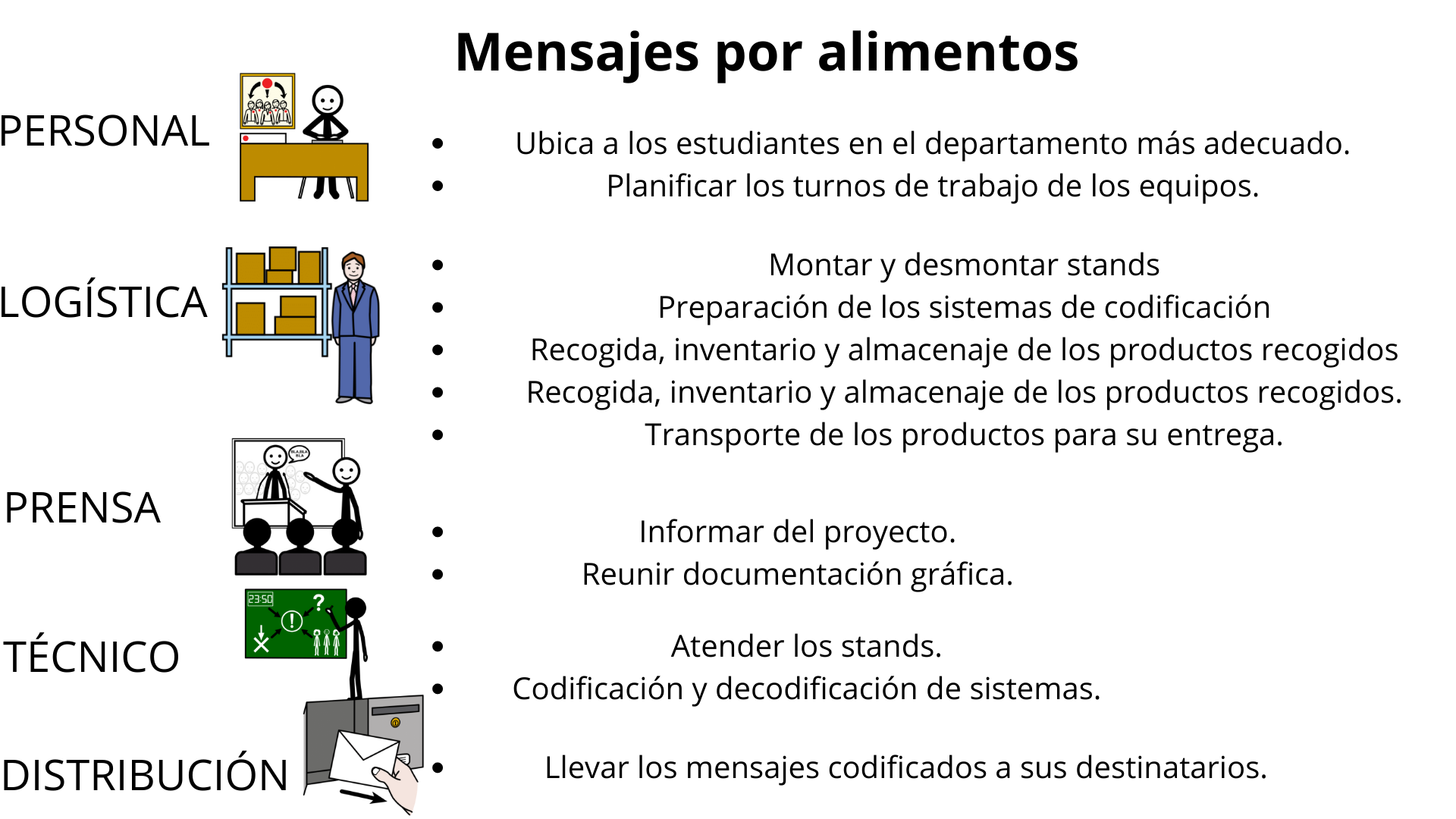
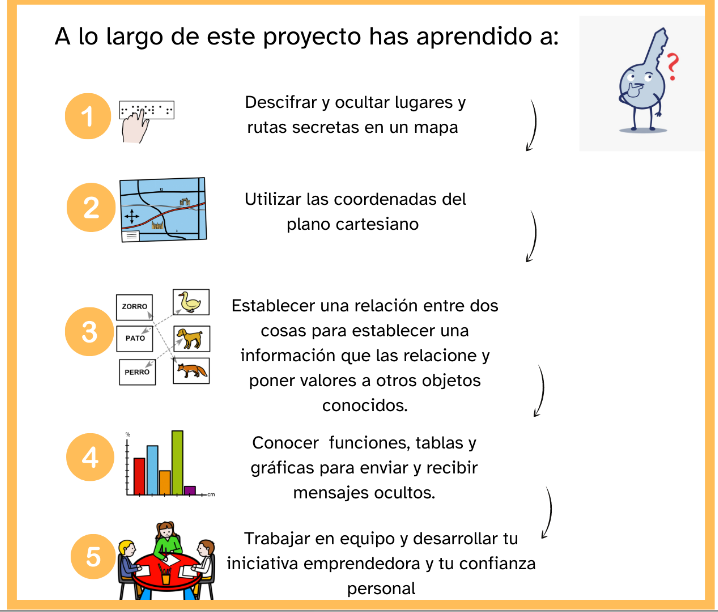
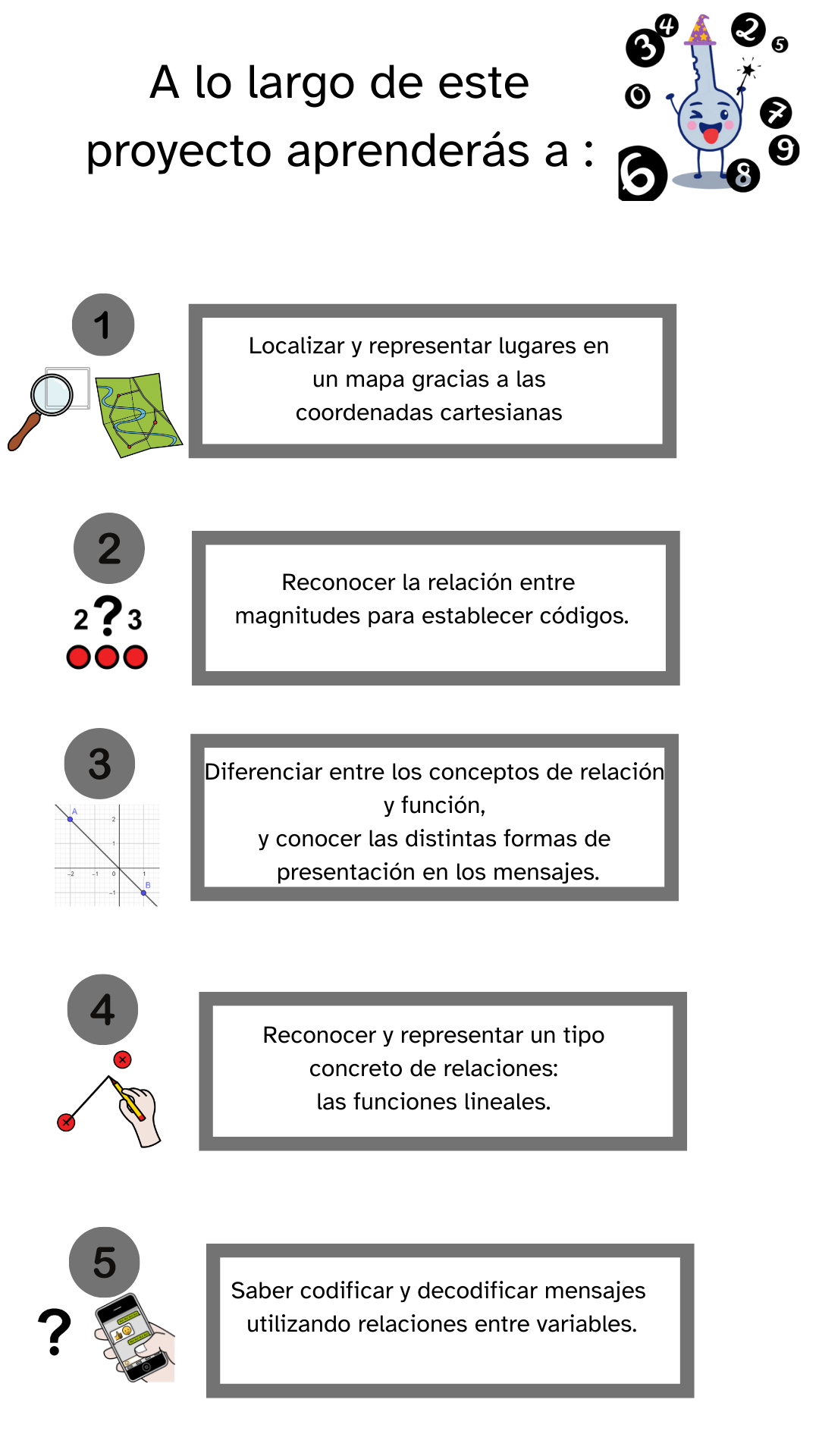
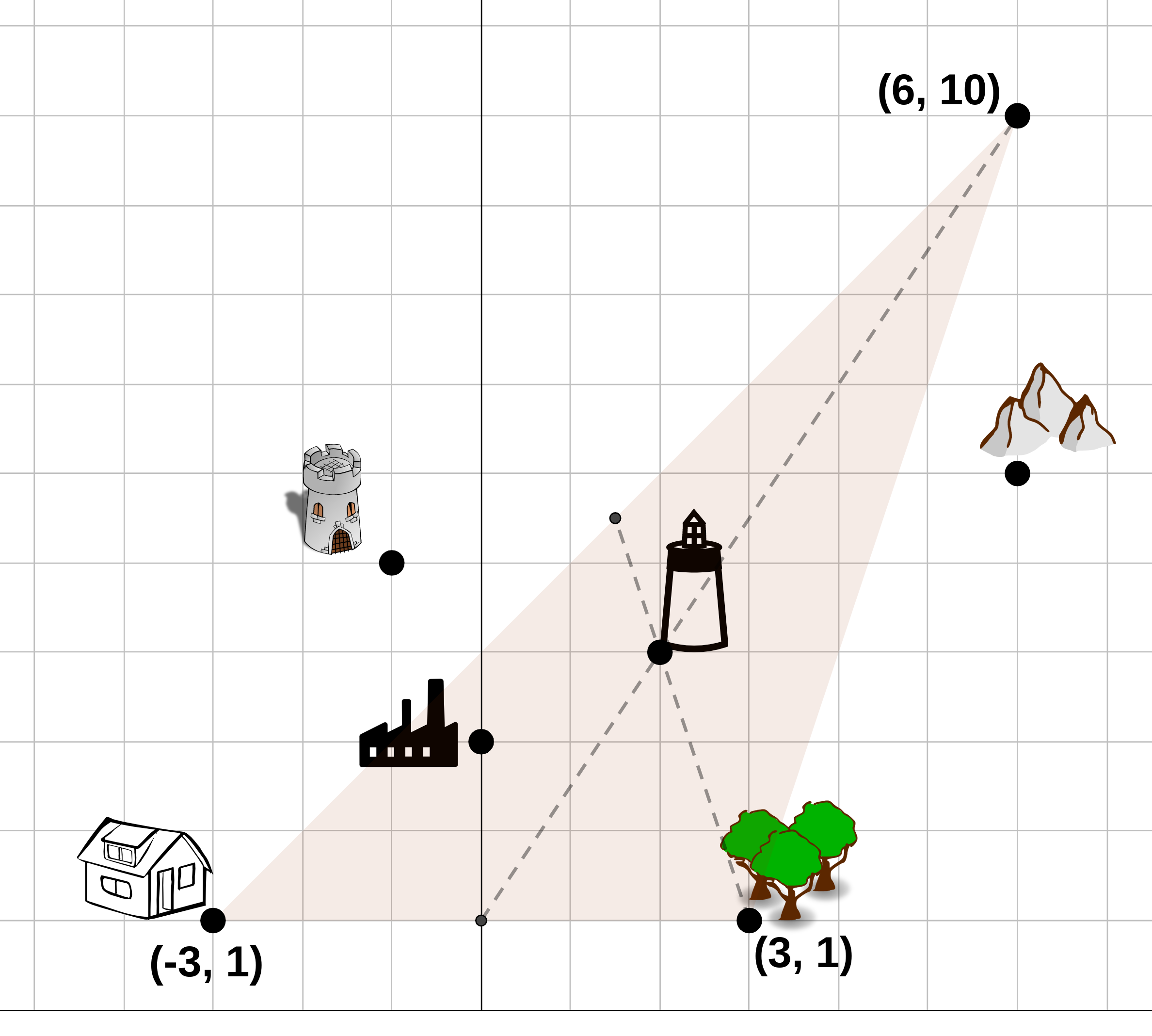
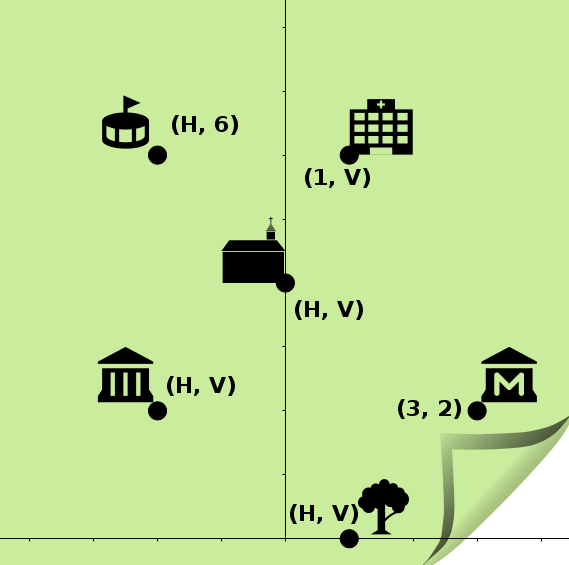
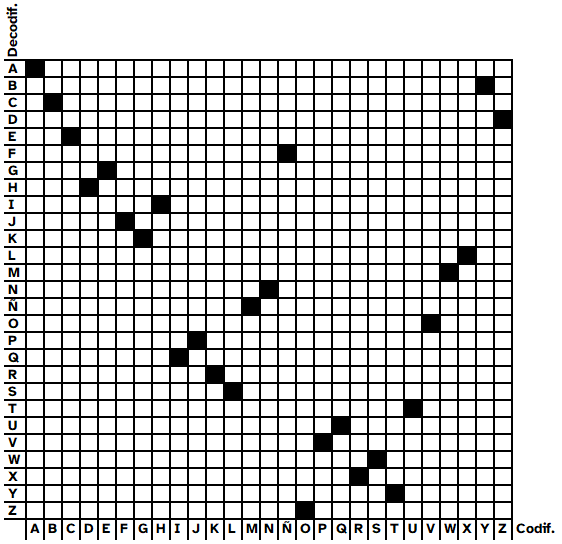
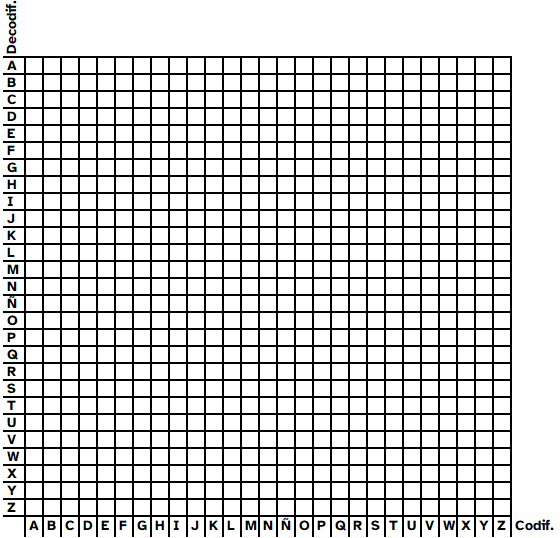
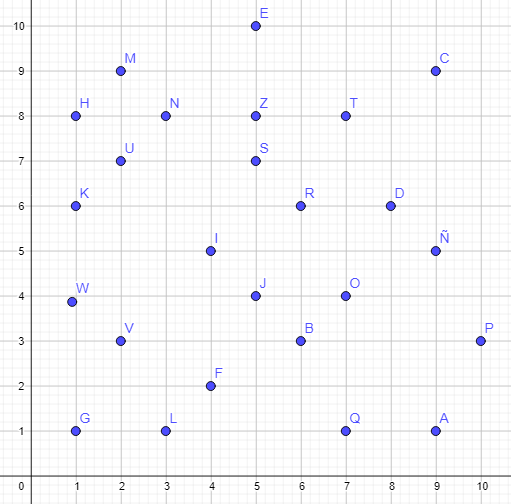
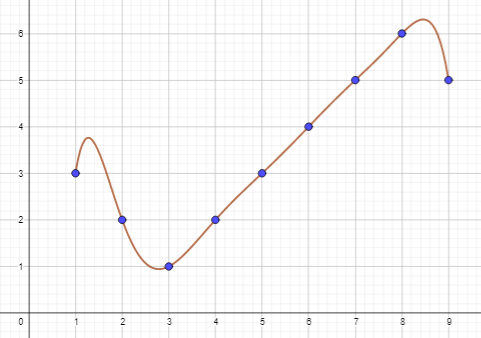
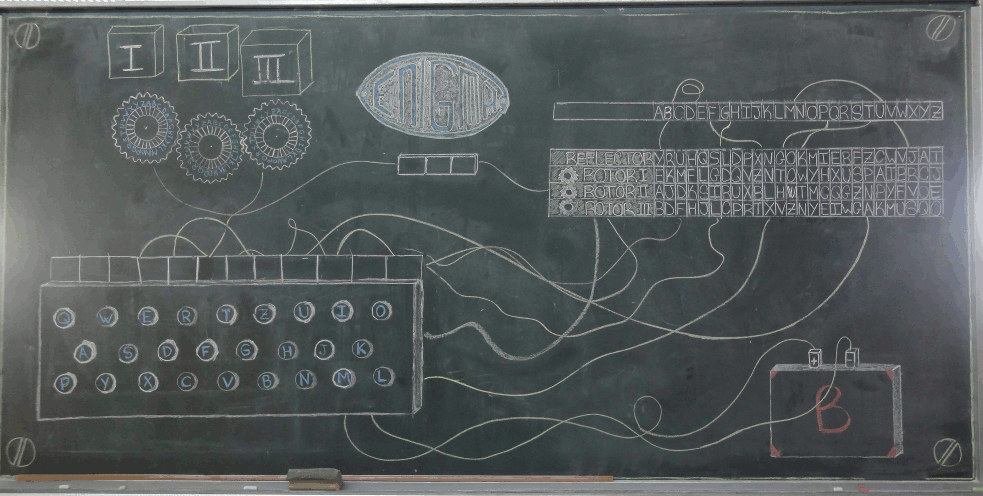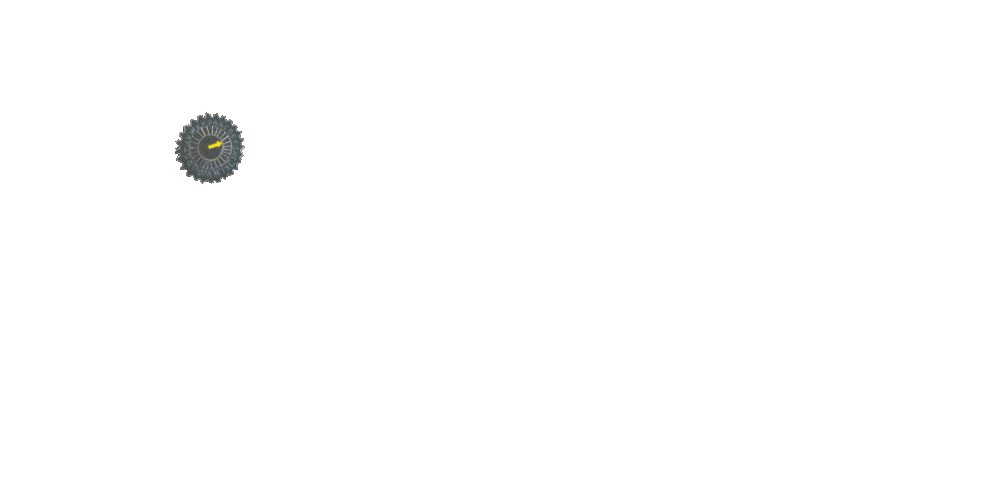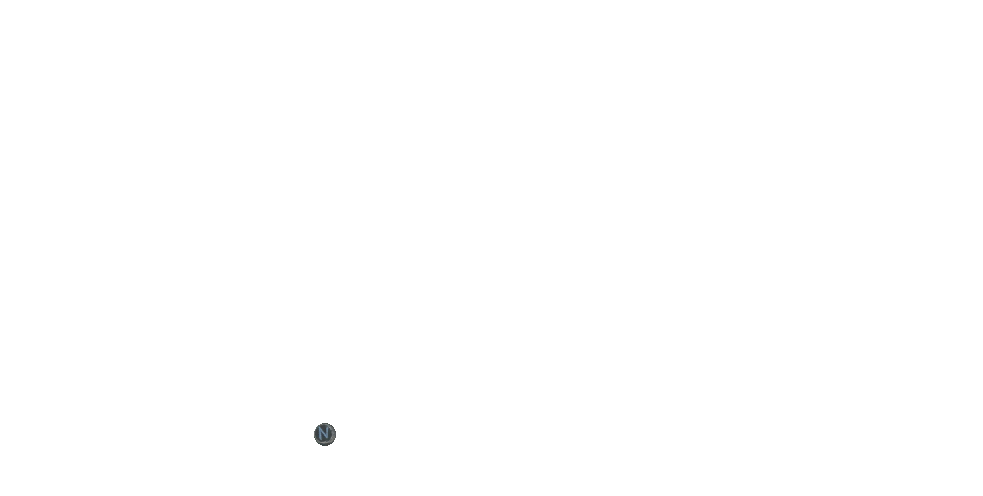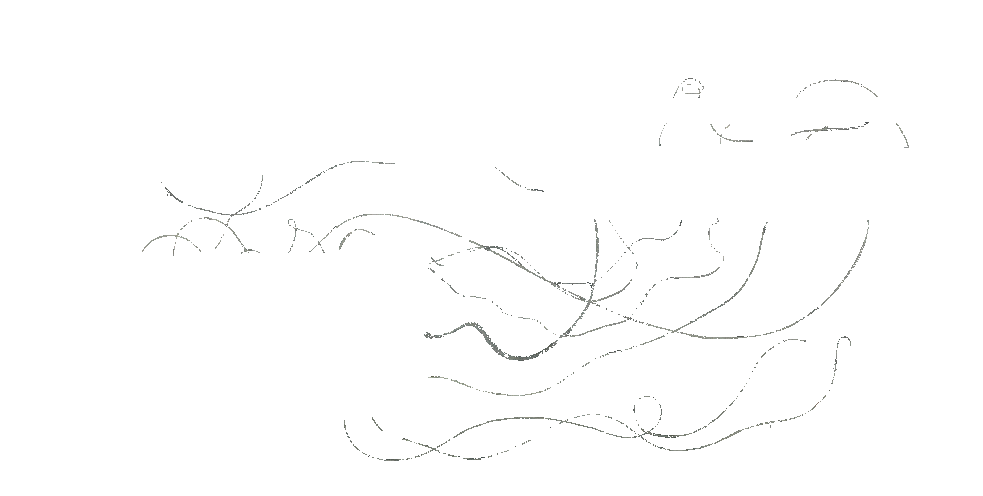
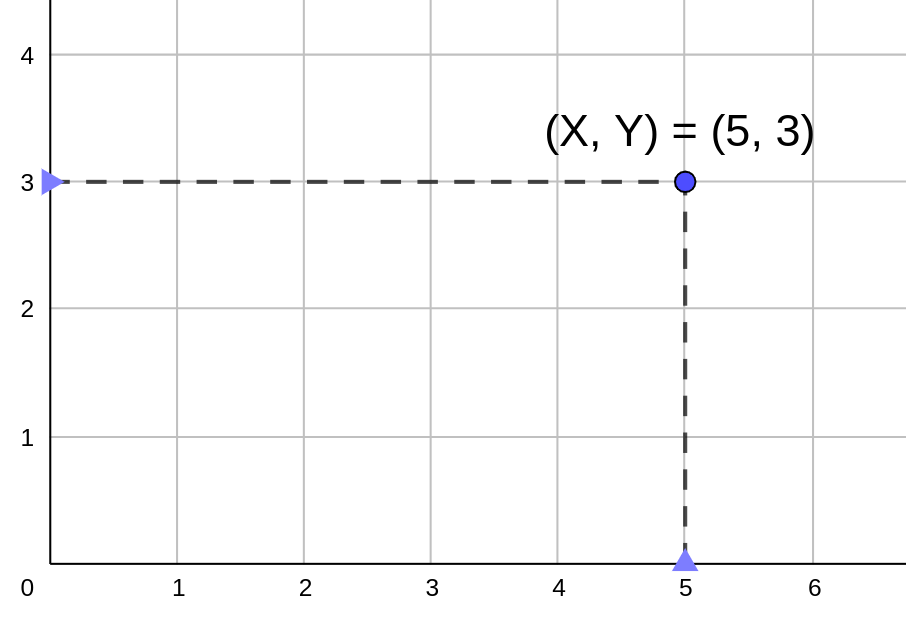
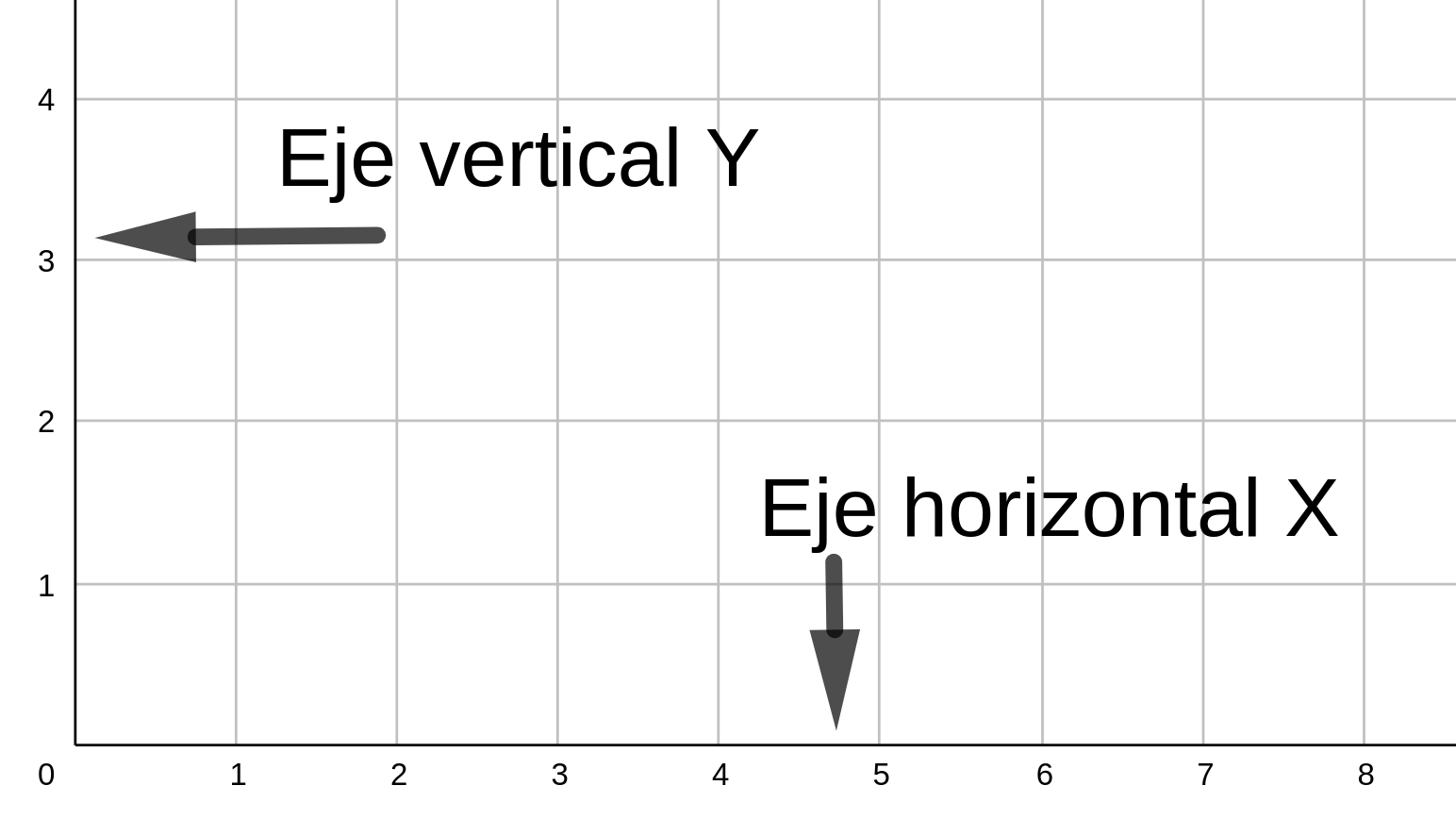
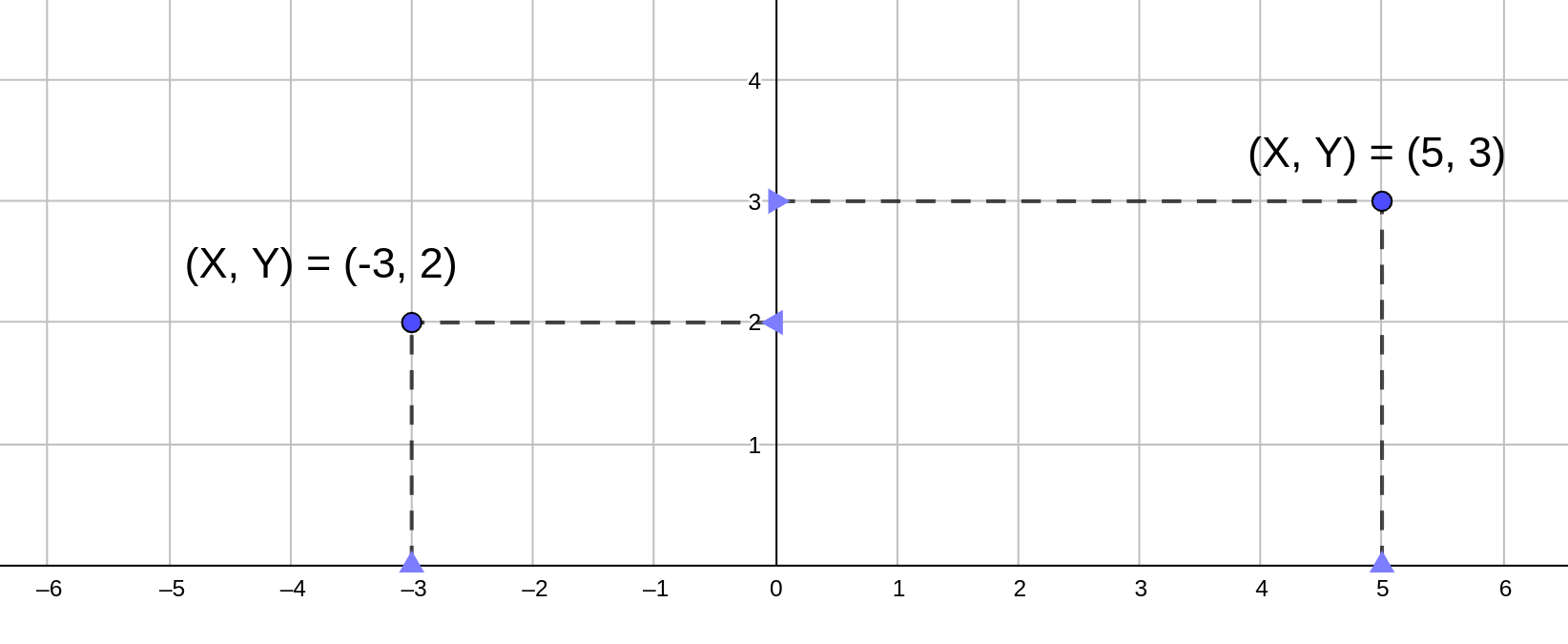
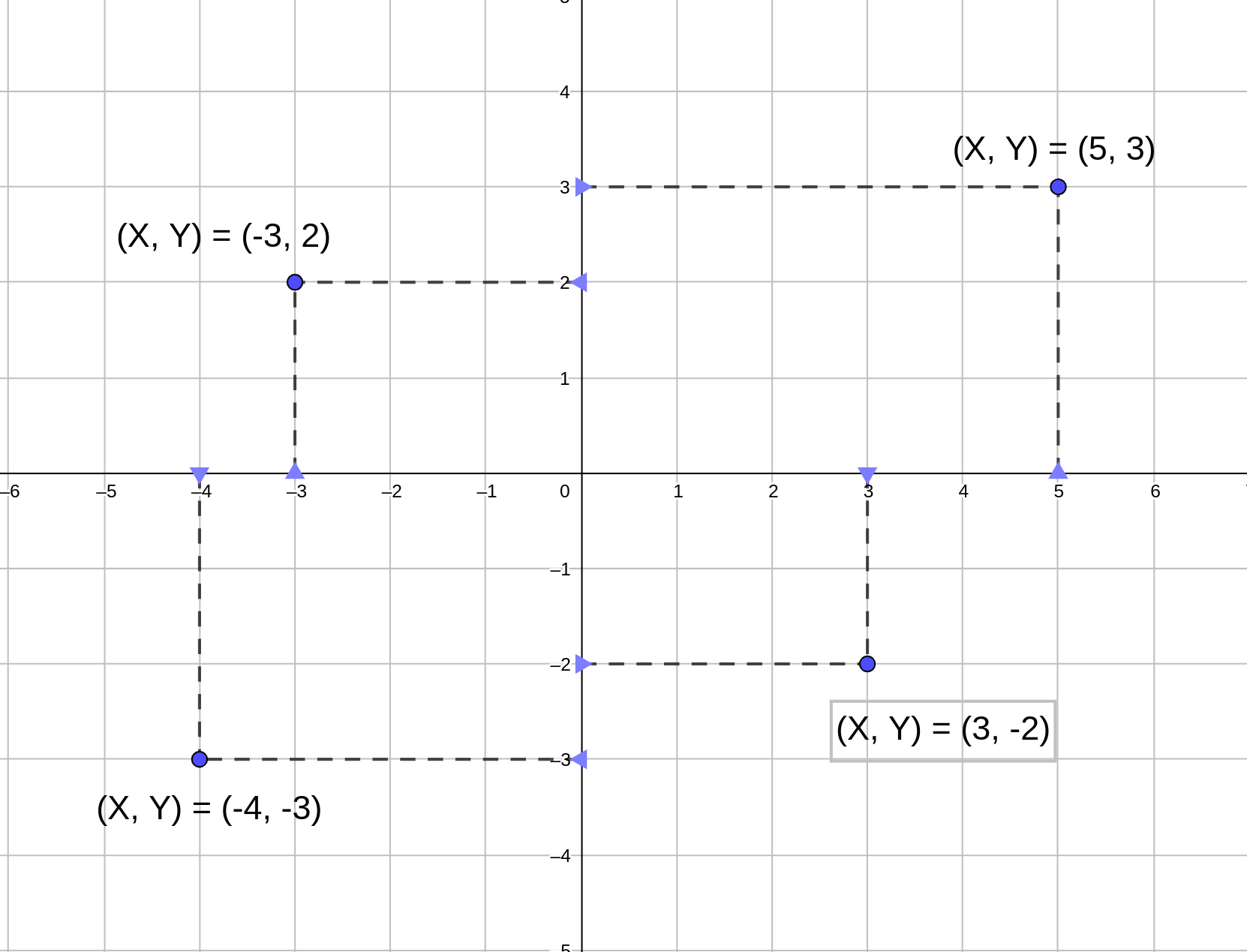
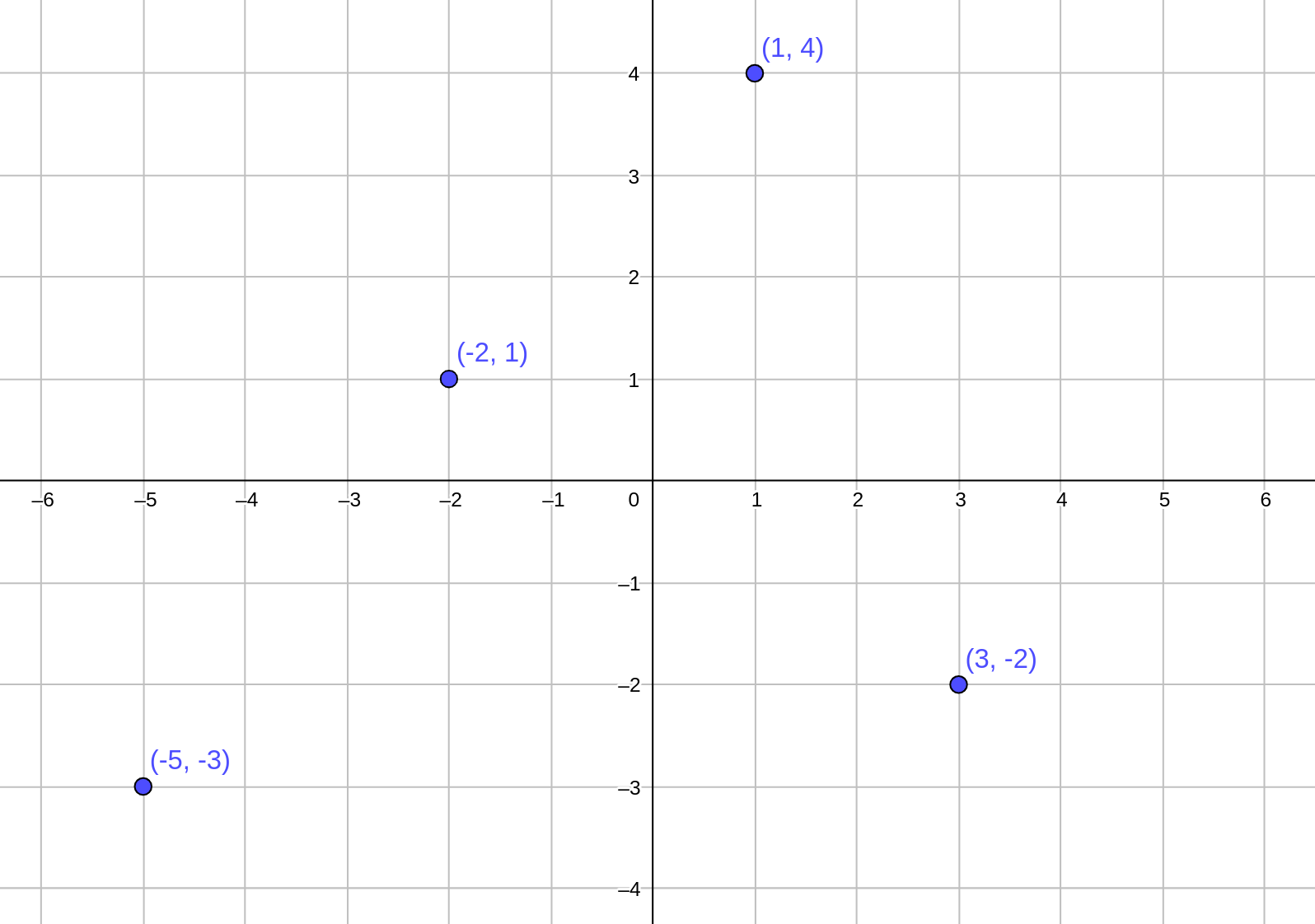
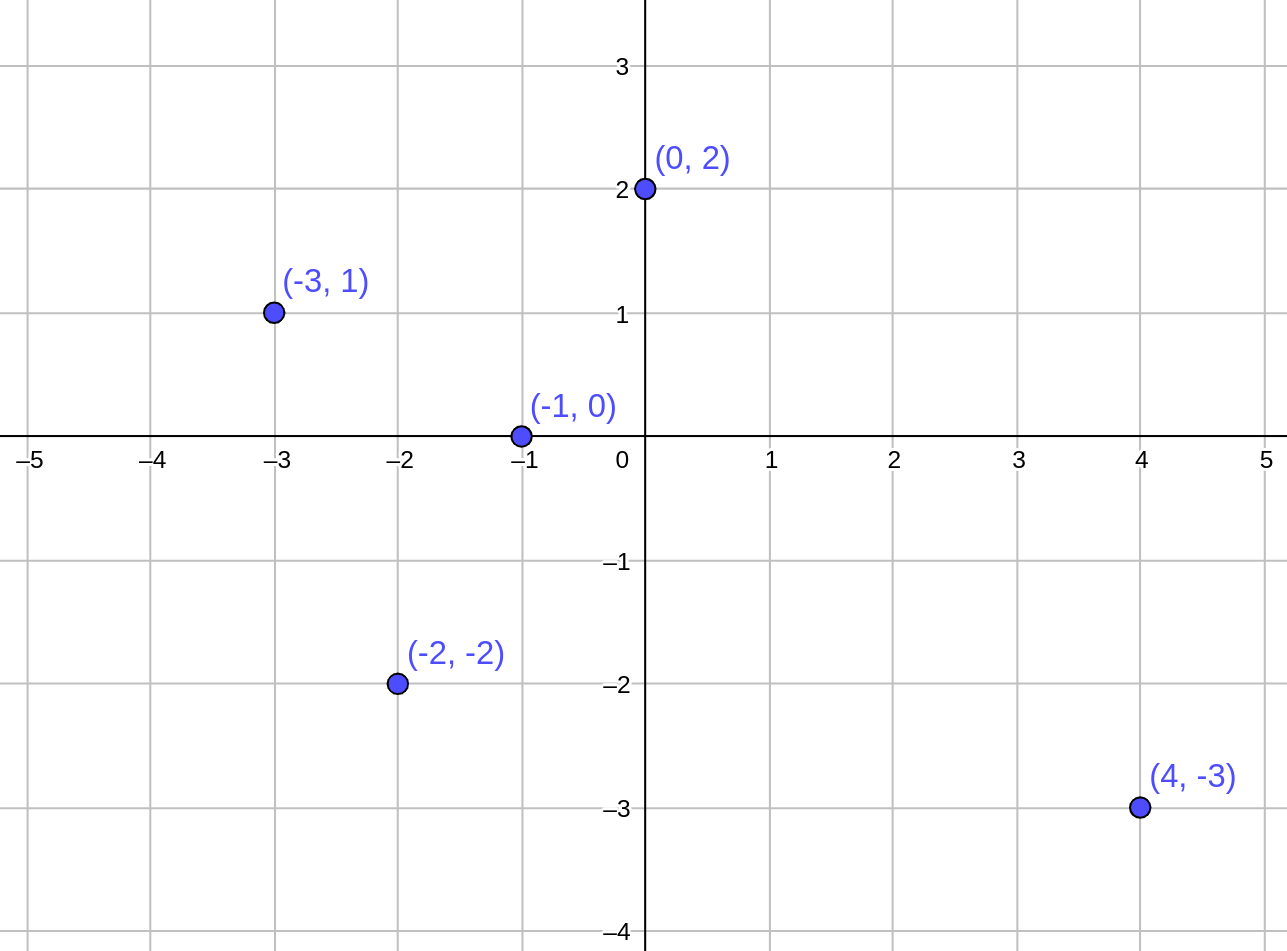
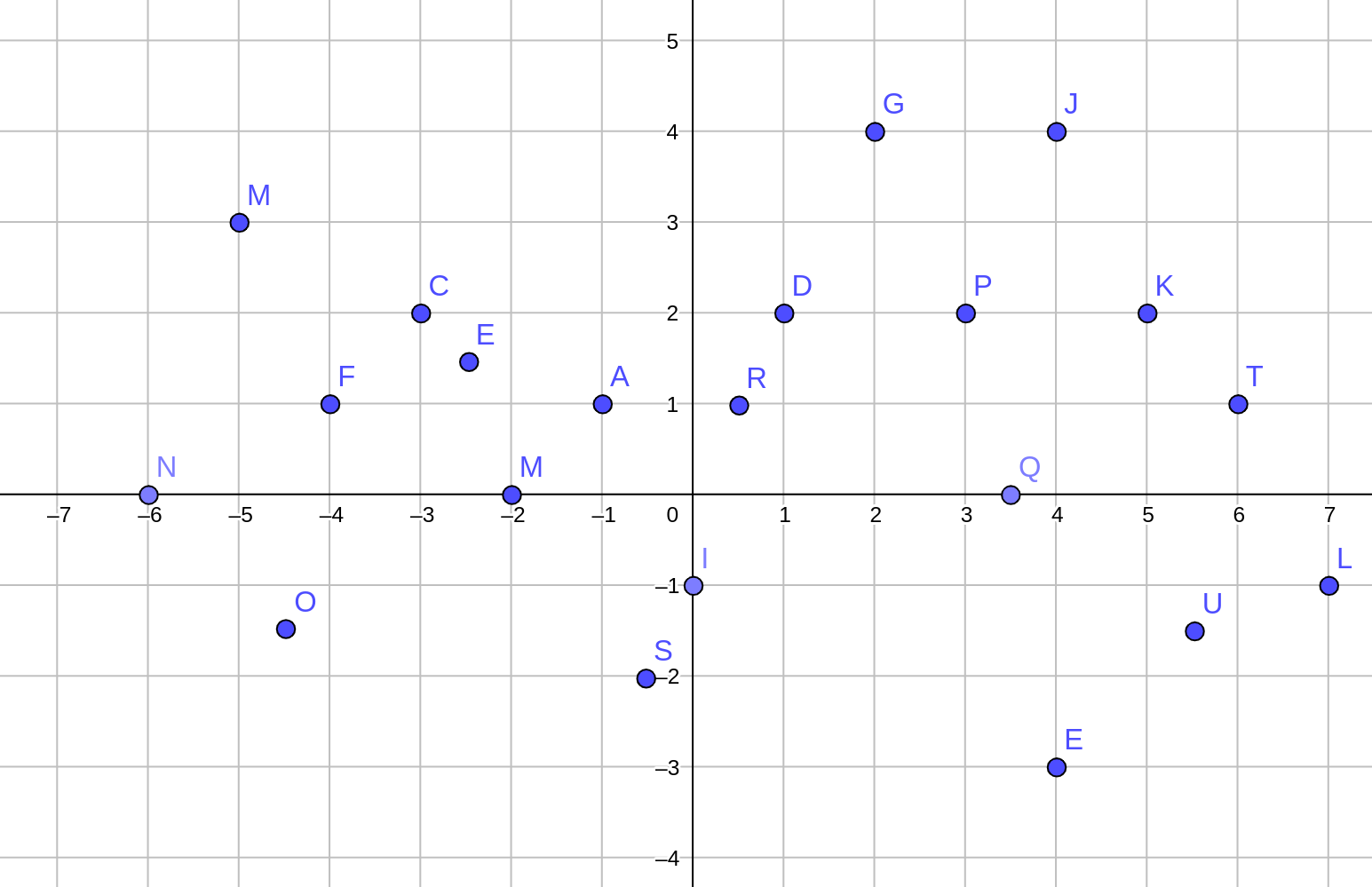
Descripción En esta secuencia didáctica para alumnos de Primer Ciclo de Matemáticas de Educación Secundaria Obligatoria se vincula el proceso relacionado con la creación de mensajes secreto, con los conceptos matemáticos de relación y función, además de utilizarse la representación de puntos en el plano cartesiano.
Persona elaboradora de contenido Diego Moreno Roldán
Persona elaboradora de contenido Miguel Ángel Frías Gallardo
Persona elaboradora de contenido Álvaro Molina Ayuso
Persona elaboradora de contenido Gema Sánchez Gómez
Persona de soporte técnico Encarnación Amaro Parrado
Persona coordinadora del ciclo José Joaquín Yelo Carrasco
Persona coordinadora de la materia Juan Francisco Romero del Castillo
Organización Dirección General de Formación del Profesorado e Innovación Educativa. Consejería de Educación y Deporte. Junta de Andalucía.
Licencia Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0

Este contenido fue creado con eXeLearning, el editor libre y de fuente abierta diseñado para crear recursos educativos.

Logo Andalucía se mueve con Europa

2. Créditos de los recursos externos

Página 1

La imagen muestra la portada de todos los REAS de Matemáticas de 1º , 2º y 3º ESO
Elaboración propia (CC BY-NC-SA)

Página 2

Elaboración Propia. Vídeo introducción Mensajes Secretos (CC BY-NC-SA)
La imagen muestra los objetivos del REA 5 de Matemáticas de 1º ESO
Elaboración propia. Objetivos Mensajes Secretos (CC BY-NC-SA)
Elaboración propia. Audio Objetivos REA Mensajes Secretos (CC BY-NC-SA)




Página 3

La imagen muestra el apoyo visual para la organización de la actividad grupal planteada.
Elaboración propia . Organización de actividad grupal (CC BY-NC-SA)
La imagen muestra un mapa con las provincias de Andalucía con cuadrículas marcadas por las divisiones de un plano cartesiano
Elaboración propia . Mapa de Andalucía en el plano (CC BY-NC-SA)
La imagen muestra un mapa de Andalucía con una ruta que pasa por Córdoba, Sevilla, Jaen, Cádiz y acaba en Almería
Elaboración propia . Mapa de andalucía con ruta (CC BY-NC-SA)
La imagen muestra un mapa de Andalucía con una ruta que pasa por Córdoba, Sevilla, Jaen, Cádiz y acaba en Almería pero con diferentes coordenadas que en la anterior imagen
Elaboración propia . Mapa de andalucía con otra ruta (CC BY-NC-SA)
En la imagen aparece un mapa con un bosque, una torre, uans montañas, una casa de campo grande y una rueda. A algunos lugares le faltan coordenadas
Elaboración propia . Mapa con coordenadas 1 (CC BY-NC-SA)
En la imagen aparece un mapa con un bosque, una torre, una casa, unas montañas y una rueda. Pero ahora el origen del mapaestá desplazado a la izquierda respecto a la anterior imagen 4 unidades
Elaboración propia . Mapa con coordenadas 2 (CC BY-NC-SA)
Mapa en el que aparecen sobre unos ejes de coordenadas un árbol en el punto (3, 1), una casa, una torre, unas montañas, un faro y una fábrica
Elaboración propia . Mapa lugares secretos (CC BY-NC-SA)
En la imagen aparece la solución la ejercicio anterior localizando el tercer punto, (6, 10), y el lugar secreto: el faro con coordenadas (2, 4)
Elaboración propia . Mapa lugares secretos con solución (CC BY-NC-SA)
En la imagen aparece unops ejes de coordenadas en los que se situan un museo en el punto (3, 2), un ayuntamiento, un estadio en altura 6, un hospital en X igual a 1, un árbol en la misma X que el hospital y sobre el eje X y una iglesia sobre el eje Y
Elaboración propia . lugares con coordenadas 3 (CC BY-NC-SA)
La imagen muestra la página 1 del diario de aprendizaje
Elaboración propia. Diario de aprendizaje página 1 (CC BY-NC-SA)
La imagen muestra un grupo de personas trabajando
Freesvg. Grupo de Trabajo (CC BY-NC-SA)
En la imagen aparece un mapa en los que se situan un museo, un ayuntamiento, un estadio, un hospital, un árbol y una iglesia.
Elaboración propia. Mapa mudo (CC BY-NC-SA)

Página 4

La imagen muestra el apoyo visual de la actividad grupal.
Elaboración propia. apoyo visual (CC BY-SA)
Imagen de un jeroglífico que podemos encontrar en el museo del Louvre
Wikimedia. Jeroglífico (CC BY-NC-SA)
La imagen muestra una codificación que asigna a cada letra un símbolo que podemos encontrar en los jeroglíficos egipcios.
Deposit photos. Codificación con jeroglíficos (CC BY-SA)
Muestra un código formado por seis símbolos egipcios
Elaboración propia a partir de una imagen Deposit photos. Jeroglífico de un superhéroe (CC BY-SA)
La imagen muestra un teclado con las letras en una posición diferente a los teclados normales.
Wikipedia. Teclado modificado (Dominio público)
La imagen muestra una cuadricula con las letras del alfabeto por filas (decodificación) y por columnas (codificación), marcando una casilla por fila y columna que relaciona las letras para establecer el código
Elaboración propia. Código en cuadricula (CC BY-NC-SA)
La imagen muestra una cuadricula con las letras del alfabeto por filas (decodificación) y por columnas (codificación), que permite marcar una casilla por fila y columna que relacione las letras para establecer el código
Elaboración propia. Cuadrícula para código en blanco (CC BY-NC-SA)
La imagen muestra unos ejes de coordenadas con puntos que tienen cada uno asignada una letra del alfabeto.
Elaboración propia. Código punto-letra (CC BY-NC-SA)
En la imagen se muestra una gráfica en la que se destacan los puntos (1,3),(2,2),(3,1),(4,2),(5,3),(6,4),(7,5),(8,6) y (9,4)
Elaboración propia. Gráfica mensaje (CC BY-NC-SA)
La imagen muestra un código QR
Wikimedia Commonos. Código QR (CC BY-NC-SA)
La imagen muestra como se escriben las letras en código Braille
Wikimedia. Braille (CC BY-NC-SA)
La imagen muestra un rectángulo de tres filas y dos columnas de puntos
Wikimedia. rectángulo Braille (CC BY-NC-SA)
La imagen muestra como se escriben los números en código Braille
Jose Miguel Gil Angulo-Agrega. Números en Braille (CC BY-NC-SA)
La imagen muestra como se escribe cada letra en código morse
wikimedia. Código morse (CC BY-NC-SA)
La imagen muestra una máquina para escribir el código Morse
Wikimedia. Máquina Morse (CC BY-NC-SA)
En la imagen se muestra la página 2 del Diario de Aprendizaje
Elaboración propia. Página 2 del diario de aprendizaje (CC BY-NC-SA)



La imagen muestra un sello de correos con la imagen del matemático Alan Turing
Flickr. Alan Turing (CC BY-NC-SA)
La imagen muestra la máquina Bombe
wikimedia. Máquina Bombe (Dominio público)
La imagen muestra a la máquina Enigma
Wikipedia. Máquina enigma (Dominio público)
La imagen muestra los rotores de la máquina Enigma
Wikipedia. Rotores (CC BY-NC-SA)
La imagen muestra el funcionamiento de la máquina enigma como gif animado
todolibroantiguo. Máquina Enigma (CC BY-NC-SA)

Página 5

La imagen muestra al matemático llamado Leibnitz
Wikimedia. Gottfried Leibnitz (Dominio público)

Página 6

La imagen muestra las coordenadas del punto (5, 3)
Elaboración propia . Punto1 (CC BY-NC-SA)
La imagen muestra los dos ejes de coordenadas, horizontal y vertical, X e Y
Elaboración propia . Ejes de coordenadas (CC BY-NC-SA)
La imagen muestra dos puntos en el plano, (5, 3) y (-3, 2)
Elaboración propia . Punto2 (CC BY-NC-SA)
La imagen muestra cuatro puntos en el plano, (5, 3), (-3, 2), (-4, -3) y (3, -2)
Elaboración propia . Punto3 (CC BY-NC-SA)
En la imagen aparecen cuatro puntos representados en el plano: (1, 4), (-2, 1), (-5, -3) y (3, -2).
Elaboración propia . 4puntos (CC BY-NC-SA)
En la imagen aparecen cinco puntos representados en el plano: (0,2), (-1, 0), (-3, 1), (-2,-2) y (4, -3)
Elaboración propia . 5puntos (CC BY-NC-SA)
En la imagen aparecen muchos puntos en el plano, cada uno con una letra
Elaboración propia . mensaje (CC BY-NC-SA)
En la imagen a parece una tabla con coordenadas X e Y de los puntos (1,4), (-2, 1), (-5, -3) y (3, -2)
Elaboración propia . tabla 1 (CC BY-NC-SA)
En la imagen aparece una tabla con coordenadas X e Y para escribir los puntos: 4, -3; 0, 2; -3, 1;-2,-2;-1,0
Elaboración propia. Tabla 2 (CC BY-NC-SA)
La imagen muestra al matemático Descartes
Wikimedia. Descartes (Dominio público)
La imagen muestra un eje de coordenadas con puntos dibujado en él
Elaboración propia. Eje de ooordenadas (CC BY-NC-SA)
La imagen muestra la estrategia cognitiva sobre cómo identificar ideas principales e ideas secundarias.
Elaboración propia. Estrategía metacognitiva (CC BY-NC-SA)

Página 7

La imagen muestra dos conjuntos y se asigna mediante flechas, a cada letra un símbolo de los jeroglíficos egipcios.
Elaboración propia. Relación con jeroglíficos (CC BY-SA)
La imagen muestra una tabla de valores y se asigna, a cada letra un símbolo de los jeroglíficos egipcios.
Elaboración propia. Tabla con jeroglíficos (CC BY-SA)
La imagen muestra una lista de pares de letras y símbolos de los jeroglíficos egipcios.
Elaboración propia. Pares ordenados con jeroglíficos (CC BY-SA)
Se ve una imagen animada con dos conjuntos, y se asigna mediante flechas a cada letra un símbolo de los jeroglíficos egipcios, y va cambiando el símbolo asignado.
Elaboración propia. relacion liosa (CC BY-SA)
En la imagen se ve una tabla con letras y símbolos en celdas coloreadas de distintos colores para crear un código
Elaboración propia. Código de colores (CC BY-SA)
En esta imagen se ve una tabla con dos columnas, en la primera hay letras o símbolos y en la segunda colores distintos, y representa un código de colores
Elaboración propia. Tabla código de colores (CC BY-SA)
En la imagen se ve una máquina en la que entran letras o símbolos y salen colores. Es una representación de lo que es el concepto de función.
Elaboración propia. Máquina función (CC BY-SA)
En la imagen se ve un diagrama de flechas en el que cada una de las vocales está asociada con un color distinto. Pero hay un color que no está asociado con ninguna vocal, y otro que está asociado con dos
Elaboración propia. uno a uno (CC BY-SA)
En la imagen se ve un diagrama de fechas en el que cada una de las vocales está asociada con un color distinto. Es un ejemplo de función uno a uno
Elaboración propia. unoauno1 (CC BY-SA)
En la imagen se ve un diagrama de fechas en el que cada una de las vocales está asociada con un color distinto, y un color sin relacionar. Es un ejemplo de función uno a uno
Elaboración propia. unoauno2 (CC BY-SA)
En la imagen se ve un diagrama de fechas en el que cada una de las vocales está asociada con un color distinto, excepto la A que está asociada con dos colores a la vez.
Elaboración propia. nofuncion (CC BY-SA)
En la imagen se ve un diagrama de fechas en el que cada una de las vocales está asociada con el mismo color. Es un ejemplo de función constante
Elaboración propia. funcion constante (CC BY-SA)
En esta imagen se ve una tabla con dos columnas de números, encabezadas por las letras x e y, en la primeraestán los números del 1 al 5 y en la segunda igual. Se indica con puntos suspensivos que la tabla es infinita y asocia a cada número el mismo número.
Elaboración propia. tabla constante (CC BY-SA)
En esta imagen se ve una tabla con 12 filas y 11 columnas. En la primera columna, aparecen de abajo arriba, los números naturales de 0 a 11 y acaba con puntos suspensivos, en la última fila aparecen de izquierda a derecha, los números naturales de 0 a 10 y acaba también con puntos suspensivos. En el interior, y a modo de diagonal, aparecen con fondo negro, las coordenadas cartesianas de los puntos desde el (1,2) al (10,11).
Elaboración propia. Grafica diagonal (CC BY-SA)
En la imagen se ve una máquina en la que entran x y x más 1. Es una representación de lo que es el concepto de función lineal que a cada número asigna el siguiente.
Elaboración propia. Maquina x mas 1 (CC BY-SA)
En la imagen se ve un sistema de coordenadas cartesianas en el que aparece una flecha verde, en posición ascendente, en la diagonal.
Elaboración propia. Grafica diagonal verde (CC BY-SA)
En la imagen aparecen seis descripciones de funciones. En la primera una tabla de valores que relaciona letras con colores, en la segunda un conjunto de cuatro puntos expresado en coordenadas cartesianas del plano, en el tercero, dos conjuntos relacionados con flechas uno a uno, en el cuarto, dos conjuntos relacionados con flechas, con una letra relacionada con dos símbolos distintos y un símbolo relacionado con dos letras, en el quinto una gráfica cuyos puntos son pelotas de baloncesto simulando el pase con dos botes, y en el sexto una tabla de valores.
Elaboración propia. Representaciones de una función (CC BY-SA)
En esta imagen se ve la pantalla principal de un geogebra, en la que aparece Clavis arriba a la izquierda diciendo que codifiques la siguiente palabra utilizando el cifrado A-G, la palabra es hablar, en la derecha aparece la doble rueda con el cifrado A-G y abajo a la izquierda aparecen dos botones, uno pone corregir, y otro pone otra palabra.
Elaboración propia. Geogebra cifrado (CC BY-SA)
En este imagen se representa la gráfica del ritmo cardiaco.
pixabay. ritmo cardiaco (CC BY-SA)
En esta imagen se representa a gente haciendo ejercicio físico.
pixabay. ejercicio fisico (CC BY-SA)
La imagen muestra la portada de las pruebas Pisa 2013
INEE y OCDE. Pruebas Pisa 2013 (CC BY-NC-SA)

Página 8

La imagen muestra una cuadricula con las letras del alfabeto por filas (decodificación) y por columnas (codificación), que permite marcar una casilla por fila y columna que relacione las letras para establecer el código, a cada letra le hace corresponder la que ocupa tres posiciones más
Elaboración propia . Código Cesar en cuadrícula (CC BY-NC-SA)
La imagen muestra a Alba en el punto (-3, 3), a Pedro en el punto (-1,3), al Betis en el punto (1,3), al Málaga en el punto (-2,1), al Cádiz en el punto (5,1), al Sevilla en el punto (4,-2), a Juan en el punto (-2,-3), a Gloria en el punto (1,-3). Además aparecen las expresiones algebráicas y=2x+1, y=-2x-3, y=-x-2, y=x+4
Elaboración propia . Equipos y amigos 1 (CC BY-NC-SA)
La imagen muestra a Alba en el punto (-3, 3), a Pedro en el punto (-1,3), al Betis en el punto (1,3), al Málaga en el punto (-2,1), al Cádiz en el punto (5,1), al Sevilla en el punto (4,-2), a Juan en el punto (-2,-3), a Gloria en el punto (1,-3). Además aparecen las expresiones algebráicas y=2x+1, y=-2x-3, y=-x-2, y=x+4. Por último viene marcado en rojo el punto (-1,-1)
Elaboración propia . Equipos y amigos 2 (CC BY-NC-SA)
La imagen muestra a Alba en el punto (-3, 3), a Pedro en el punto (-1,3), al Betis en el punto (1,3), al Málaga en el punto (-2,1), al Cádiz en el punto (5,1), al Sevilla en el punto (4,-2), a Juan en el punto (-2,-3), a Gloria en el punto (1,-3). Además aparecen las expresiones algebráicas y=2x+1, y=-2x-3, y=-x-2, y=x+4. Por último viene marcado en rojo los puntos (-1,-1) y (2,5)
Elaboración propia . Equipos y amigos 3 (CC BY-NC-SA)
La imagen muestra a Alba en el punto (-3, 3), a Pedro en el punto (-1,3), al Betis en el punto (1,3), al Málaga en el punto (-2,1), al Cádiz en el punto (5,1), al Sevilla en el punto (4,-2), a Juan en el punto (-2,-3), a Gloria en el punto (1,-3). Además aparecen las expresiones algebráicas y=2x+1, y=-2x-3, y=-x-2, y=x+4. Por último viene marcado en rojo la recta que une los puntos (-1,-1) y (2,5)
Elaboración propia . Equipos y amigos 4 (CC BY-NC-SA)
Gráfica de una recta que pasa por los puntos (-3,-1) y (0,2)
Elaboración propia . Gráfica que pasa por dos puntos 1 (CC BY-NC-SA)
Gráfica de una recta que pasa por los puntos (-2,2) y (1,-1)
Elaboración propia . Gráfica que pasa por dos puntos 2 (CC BY-NC-SA)
Muestra una recta verde creciente en unos ejes de coordenadas
Elaboración propia . Recta 1 (CC BY-NC-SA)
Muestra una recta roja decreciente en unos ejes de coordenadas
Elaboración propia . Recta 1 (CC BY-NC-SA)
La imagen muestra a la matemática Gaetana Agnesi
Wikimedia . Gaetana Agnesi (Dominio público)
La imagen muestra el paso número tres del diario de aprendizaje
Elaboración propia. Paso 3 del diario de aprendizaje (CC BY-NC-SA)

Página 9

La imagen muestra como título
Elaborado con canva. Organigrama (CC BY-NC-SA)
Muestra la palabra personal en una etiqueta con una silueta.
Elaborado con canva. Personal (CC BY-NC-SA)
Muestra la palabra logística en una etiqueta con una silueta.
Elaborado con canva. Logística (CC BY-NC-SA)
Muestra la palabra logística en una prensa con una silueta.
Elaborado con canva. Prensa (CC BY-NC-SA)
Muestra la palabra técnico en una prensa con una silueta.
Elaborado con canva. Técnico (CC BY-NC-SA)
Muestra la palabra distribución en una etiqueta con una silueta.
Elaborado con canva. Distribución (CC BY-NC-SA)
La imagen muestra el apoyo visual de la actividad en la que se reparten los roles a cada miembro del grupo.
Elaboración propia con Canva. Apoyo visual reparto de roles (CC BY-NC-SA)
La imagen muestra un smartphone escaneando un código QR
FreeSvg. Lector de códigos (Dominio público)
Se muestran los Jeroglíficos en las paredes de la tumba de Abu Simbel
Wikimedia. Jeroglíficos tumba Abu Simbel (CC BY-SA)
La imagen muestra un teclado sin teclas y las teclas en una cesta
Wikimedia. Teclado sin teclas (CC BY-SA)
La imagen muestra un rodillo de la máquina enigama en la que se muestran las relaciones entre letras para formar el código
Wikimedia. Rodillo codificación (CC BY-SA)
La imagen muestra el paso cuatro del diario de aprendizaje
Elaboración propia. Paso 4 del diario de aprendizaje (CC BY-NC-SA)

Página 10

La imagen muestra los objetivos finales del proyecto
Elaboración propia . Objetivos finales del proyecto REA 05 (CC BY-NC-SA)
La imagen muestra a Clavis megaestratega
Elaboración propia. Clavis megaestratega (CC BY-NC-SA)
La imagen muestra el apoyo visual de los objetivos finales del proyecto 1.Descifrar y ocultar lugares y rutas secretas en un mapa 2.Utilizar las coordenadas del plano cartesiano 3. Establecer una relación entre dos cosas para establecer una información que las relacione y poner valores a otros objetos conocidos. 4.Conocer funciones, tablas y gráficas para enviar y recibir mensajes ocultos.5. Trabajar en equipo y desarrollar tu iniciativa emprendedora y tu confianza personal
Elaboración propia. Objetivos finales (CC BY-NC-SA)

Página 11

Los símbolos pictográficos utilizados son propiedad del Gobierno de Aragón y han sido creados por Sergio Palao para ARASAAC (http://www.arasaac.org), que los distribuye bajo Licencia Creative Commons BY-NC-SA.

3. Historial de versiones

Elaborado por:

Servicio de Innovación Educativa de la Consejería de Educación de la Junta de Andalucía.
 Versión: 01 Fecha de publicación:
 Primera versión

3. Aquí tienes el archivo fuente para editar este REA

Icono proyecto REA Andalucía en el que puede verse representados los tres colores del Diseño Universal para el Aprendizaje

  • Esto significa que tienes la posibilidad de poder usarlo, descargarlo, redistribuirlo y modificarlo para adaptarlo a tus necesidades.
  • Sigue estos pasos para usar/redistribuir/modificar este REA:

1. Descarga el archivo fuente. Con esto tienes el recurso original en formato editable.

2. Modifícalo usando eXeLearning.

3. Si aun no lo tienes, descarga e instala el estilo EducaAnd.

4. Si lo modificas, has de reconocer la autoría y publicarlo con la misma licencia (CC BY-SA-NC).

Puedes usar esta cita para referenciarlo:

Este REA es una adaptación del recurso original "Crea tu REA con calidad: guía para personas elaboradoras" del Proyecto REA Andalucía de la Consejería de Educación y Deporte de la Junta de Andalucía, que lo distribuye bajo licencia de CC BY-SA-NC.

Descargar el fichero .elp