Diccionario
Afín
Las matemáticas de los medicamentos
4.2. ¡Ya no empezamos desde cero!
Ahora que has aprendido a manejar las funciones lineales, ya sabes más sobre medicamentos.
Estas funciones están muy relacionadas con la proporcionalidad, y se usa mucho en la administración de medicamentos.
Por ejemplo cuando la dosis depende del peso del paciente.
Recuerda que su gráfica pasa siempre por el origen de coordenadas, pero y si no fuese así.
¿Te atreves a encontrar otras fórmulas?. Nos servirán para administrar correctamente otros medicamentos. ¡Vamos a verlas!.
Lectura facilitada
Ya sabes trabajar con las funciones lineales
Y has aprendido más sobre el uso de los medicamentos.
Las funciones lineales se usan para
administrar medicamentos correctamente.
Recuerda que la dosis depende del peso del paciente
Y en la gráfica siempre pasa por el origen de las coordenadas.
Ahora vas a conocer otras fórmulas
Estas fórmulas que te van a ayudar a administrar
de forma adecuada otros medicamentos.
¡Vamos a verlas!
1. La dosis afín
Vamos a ver qué características tienen las funciones afines, que están muy relacionadas con las funciones lineales estudiadas en la página anterior.
Funciones afines
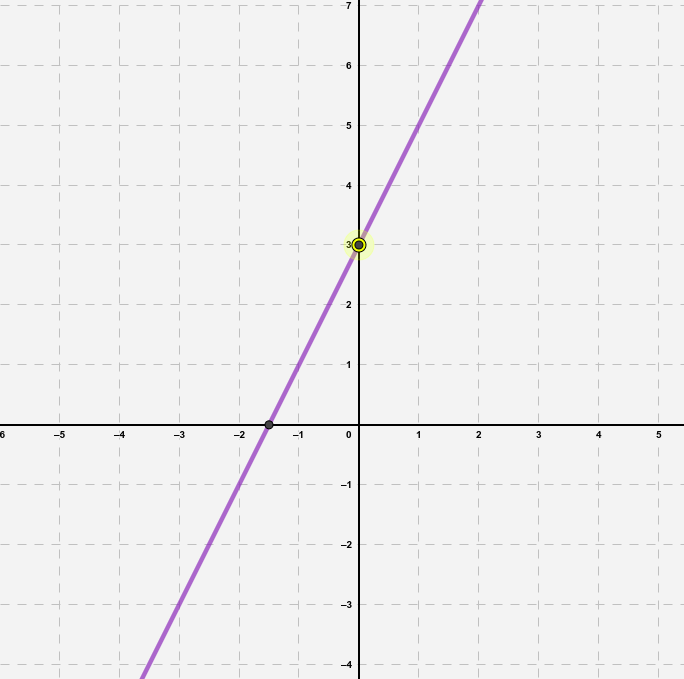
Las funciones afines están muy relacionadas con las funciones de proporcionalidad.
La diferencia fundamental está en que mientras todas las funciones de proporcionalidad pasan por el origen de coordenadas, la funciones afines no tienen tienen porque hacerlo.
En la pestañas siguientes vamos a continuar trabajando los conceptos que se iniciaron en la página anterior: pendiente y ordenada en el origen.
.
Pendiente
Como recordarás, la pendiente de la función representa su crecimiento, es decir, si va subiendo o si va bajando.
Vamos a intentar calcular la pendiente en el siguiente ejemplo:
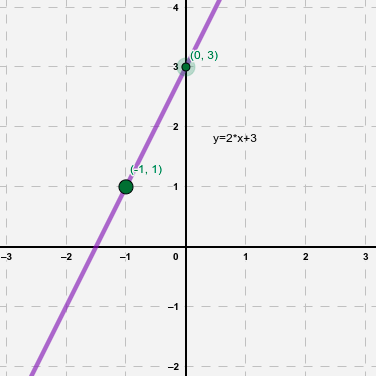
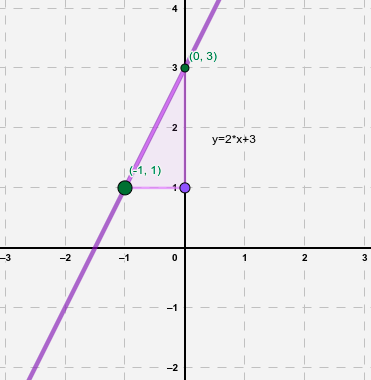
Observa, que en la imagen izquierda se han marcado dos puntos, estos son A(-1,1) y B(0,3).
En la imagen derecha se ha construido un triángulo rectángulo con esos dos puntos. La base del triángulo mide una unidad, y la altura dos unidades. La pendiente de la recta es el cociente entre la altura y la base del triángulo formado, o sea
\(pendiente\) = \( \frac{altura} {base} \) = \( \frac{2} {1} \) = \(2\)
Si te fijas en la fórmula de la función afín \(y=2x+3\), el coeficiente de \(x\) es 2, que coincide con la pendiente que acabamos de calcular
Ordenada en el origen
Todas las funciones lineales pasan por el origen de coordenadas, es cambio las funciones afines pueden cortar al eje vertical a cualquier altura.
En el ejemplo que estamos manejando, la recta corta al eje vertical a una altura de 3 unidades, usando el lenguaje matemático; la ordenada en el origen es 3.
Recuerdas que la fórmula de esta función afín es \(y=2x+3\).
Por tanto la ordenada en el origen coincide con el término independiente de la fórmula.
Definición:
Que tiene una o más cosas comunes con otro.
Ejemplo:
Mi compañero tiene un gusto muy afín a mi.
Lectura facilitada
Ahora vas a ver las características de las funciones afines.
Funciones afines
Las funciones afines están muy relacionadas con las funciones de proporcionalidad.
La diferencia es que en las funciones de proporcionalidad se pasan por el origen de coordenadas.
En las funciones afines no tienen tienen porque pasar por el eje de coordenadas.
Ahora verás lo de la página anterior:
pendiente y ordenada en el origen.
Pendiente
La pendiente de la función
representa su crecimiento
si va subiendo o si va bajando.
Vamos a intentar calcular la pendiente en el siguiente ejemplo:
Observa, que en la imagen izquierda se han marcado dos puntos, estos son A(-1,1) y B(0,3).
En la imagen derecha se ha construido un triángulo rectángulo con esos dos puntos.
La base del triángulo mide una unidad, y la altura dos unidades. La pendiente de la recta es el cociente entre la altura y la base del triángulo formado, o sea
\(pendiente\) = \( \frac{altura} {base} \) = \( \frac{2} {1} \) = \(2\)
Si te fijas en la fórmula de la función afín \(y=2x+3\), el coeficiente de \(x\) es 2, que coincide con la pendiente que acabamos de calcular
Ordenada en el origen
Todas las funciones lineales pasan por el origen de coordenadas.
Las funciones afines pueden cortar al eje vertical a cualquier altura.
En el ejemplo que estamos manejando, la recta corta al eje vertical a una altura de 3 unidades, usando el lenguaje matemático; la ordenada en el origen es 3.
Recuerdas que la fórmula de esta función afín es \(y=2x+3\).
Por tanto la ordenada en el origen coincide con el término independiente de la fórmula.
Ahora vamos a utilizar las funciones afines para aprender un poco de pensamiento computacional. Para ello utilizaremos el lenguaje de programación Scratch. Es muy intuitivo, y hay una enorme comunidad de usuarios de Scratch compartiendo sus programas.
Un programa Scratch
Para hacer funcionar el programa pulsa la bandera verde, para pararlo pulsa el botón rojo
El código del programa
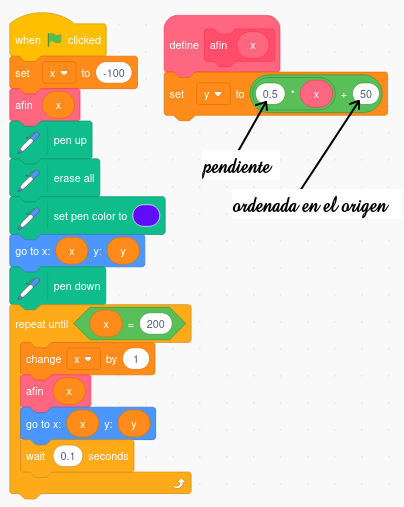El programa tiene dos partes, en la derecha vemos la construcción de una función, y en la izquierda vemos el código que la dibuja.
Construir la función:
- Se dice que se construye una función (define afin x
- Se dice que su fórmula será y=0.5x+50 set y to 0.5·x+50
Observa donde va la pendiente y la ordenada en el origen
Dibujar la función:
- Se indica el valor inicial de x=-100
- Se calcula el valor inicial de y
- Se coloca el lápiz en el punto inicial
- Se ordena que se hagan las instrucciones siguientes hasta que x llegue a 200
- Se aumenta x de uno en uno
- Se calcula su valor con la función afín
- Se desplaza el lápiz
- Y se espera 0.1 segundos para que veas como progresa
Lumen dice ¿Y si de la gráfica solo conocemos un par de puntos?
A veces las dosis no dependen directamente del peso, o de otra magnitud.
Puede ser que haya que aumentar o disminuir alguna cantidad fija. Este tipo de funciones, se llaman lineales. Vamos a concluir lo aprendido anteriormente, intentando descubrir la fórmula de una función afín a partir de un par de puntos de su tabla de valores,
Un par de puntos
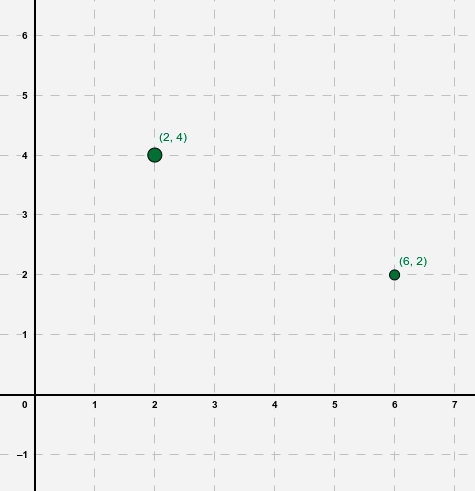
En la imagen de la izquierda tenemos un par de puntos.
Vamos a intentar aplicar lo aprendido en las pestañas anteriores para encontrar la fórmula de la función afín que pasa por los puntos A(2,4) y B(6,2)
Además, vamos a intentar que el método pueda servir sin tener que dibujar la recta que pasa por esos puntos... ¡imagínate si podrías resolver este reto dibujando rectas las coordenadas A(-1200,200) y B(457,-214)!
Descubrimos la pendiente
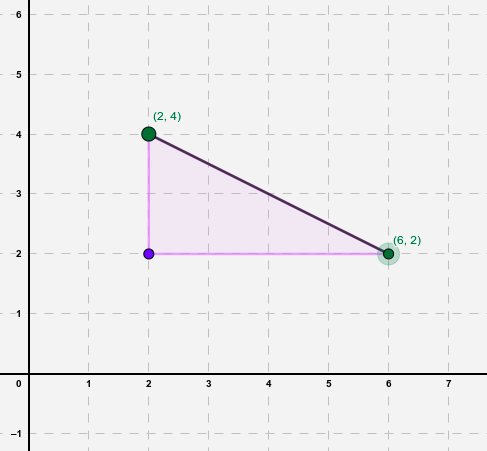Primero hemos unido los puntos A(2,4) y B(6,2) por un segmento, y después hemos cerrado un triángulo rectángulo.
Veamos la variación que se ha producido verticalmente y horizontalmente de A a B.
Verticalmente: pasamos de altura 4 en A a altura 2 en B (mira el valor de la segunda coordenada de ambos puntos), variación=2-4=-2
Horizontalmente: pasamos de un valor 2 en A a valor de 6 en B , (mira el valor de la primer coordenada de ambos puntos), variación=6-2=4
Por tanto, la pendiente es m=-2/4=-0.5
y por fin ... la fórmula
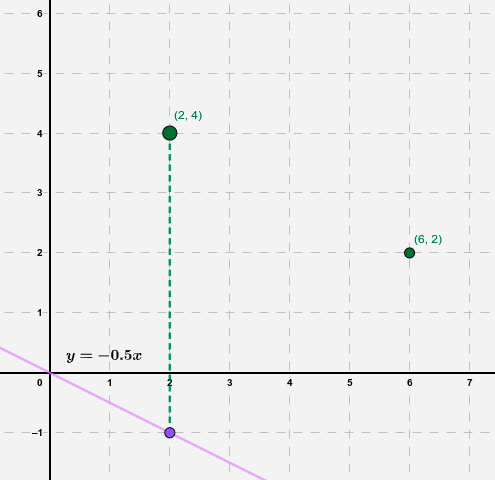Ya hemos descubierto que la pendiente es -0.5
¡La fórmula no puede ser \(y=-0.5x\) porque ya sabemos que eso en sería una función lineal que pasa por el origen de coordenadas!
Las coordenadas del punto A son (2,4). Si usamos la fórmula lineal \(y=-0.5x\) con el valor x de A obtenemos \(y\)=-0.5·2=-1. Obviamente, no ha salido el valor 4 (valor de y en el punto A).
Pero como la diferencia entre el valor \(x\) de A, 4 y -1, el valor de la fórmula lineal, es 5 (mira la gráfica de la izquierda), podemos afirmar que la fórmula es \(y=-0.5x+5\)
Luego la ordenada en el origen es 5. Traza la recta que une ambos puntos y comprueba que corta al eje vertical a esa altura.
2. Practica con la dosis afín
Ya conoces la función afín.
Está muy relacionada con la función lineal.
A continuación tienes varias actividades con las que puedes practicar tu dominio de esta función.
Realiza las que te parezcan interesantes.
¡Ánimo!
Opción A. Pendiente y ordenada en el origen
Lee cómo encontrar la pendiente y la ordenada en el origen de la función afín del siguiente ejemplo, y después realiza el ejercicio que viene a continuación.
La recta
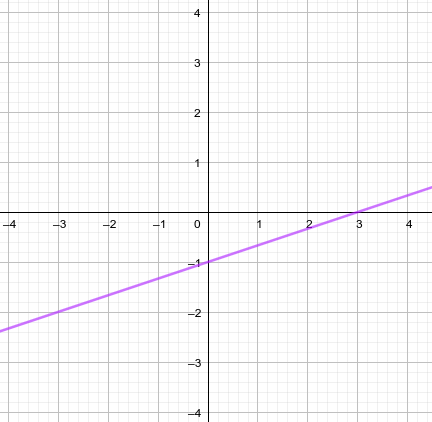
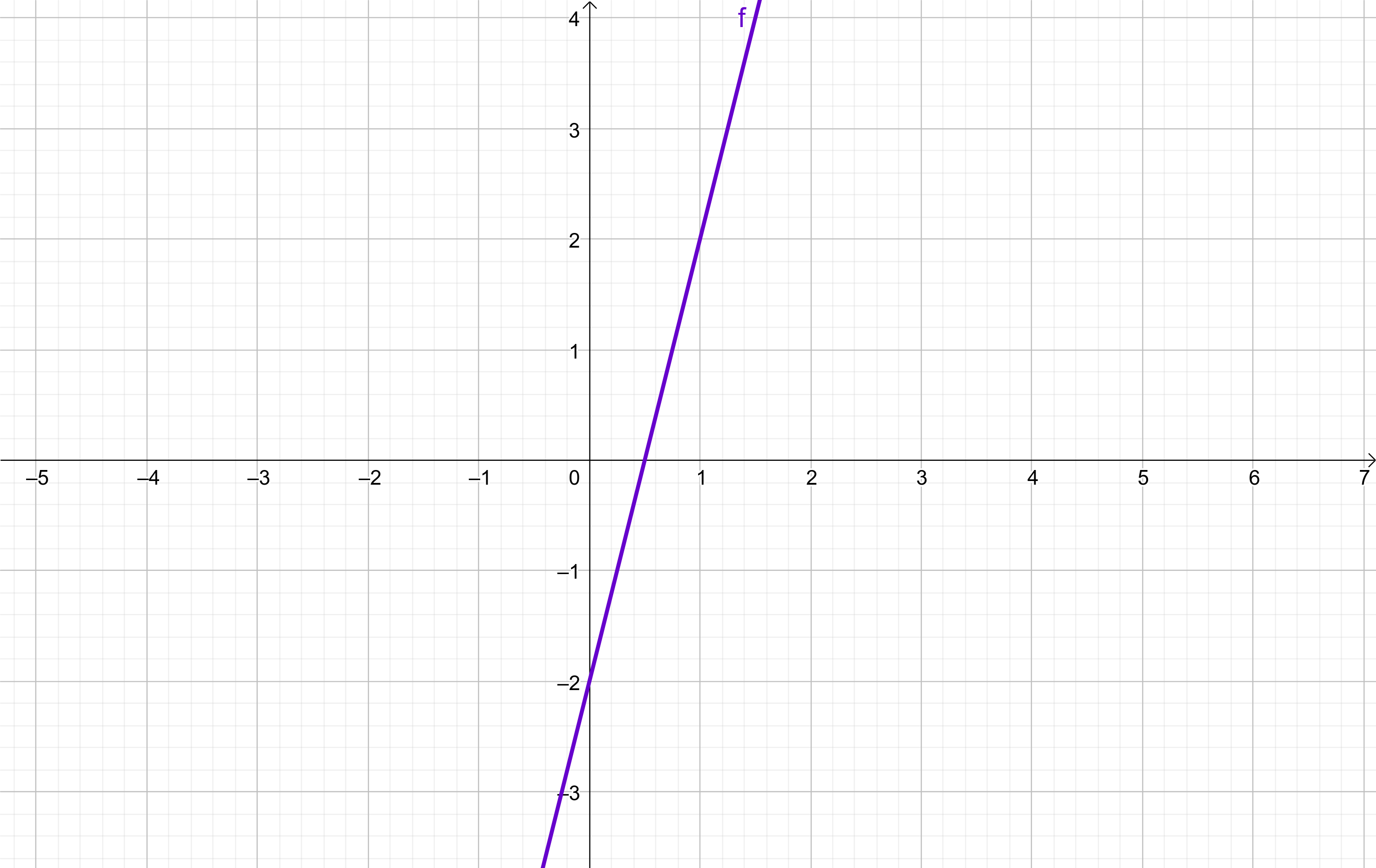Observa la gráfica de la izquierda.
Identificamos que es una función afín por las siguientes razones:
1. Es una línea recta.
2. No pasa por el origen de coordenadas.
Ordenada en el origen
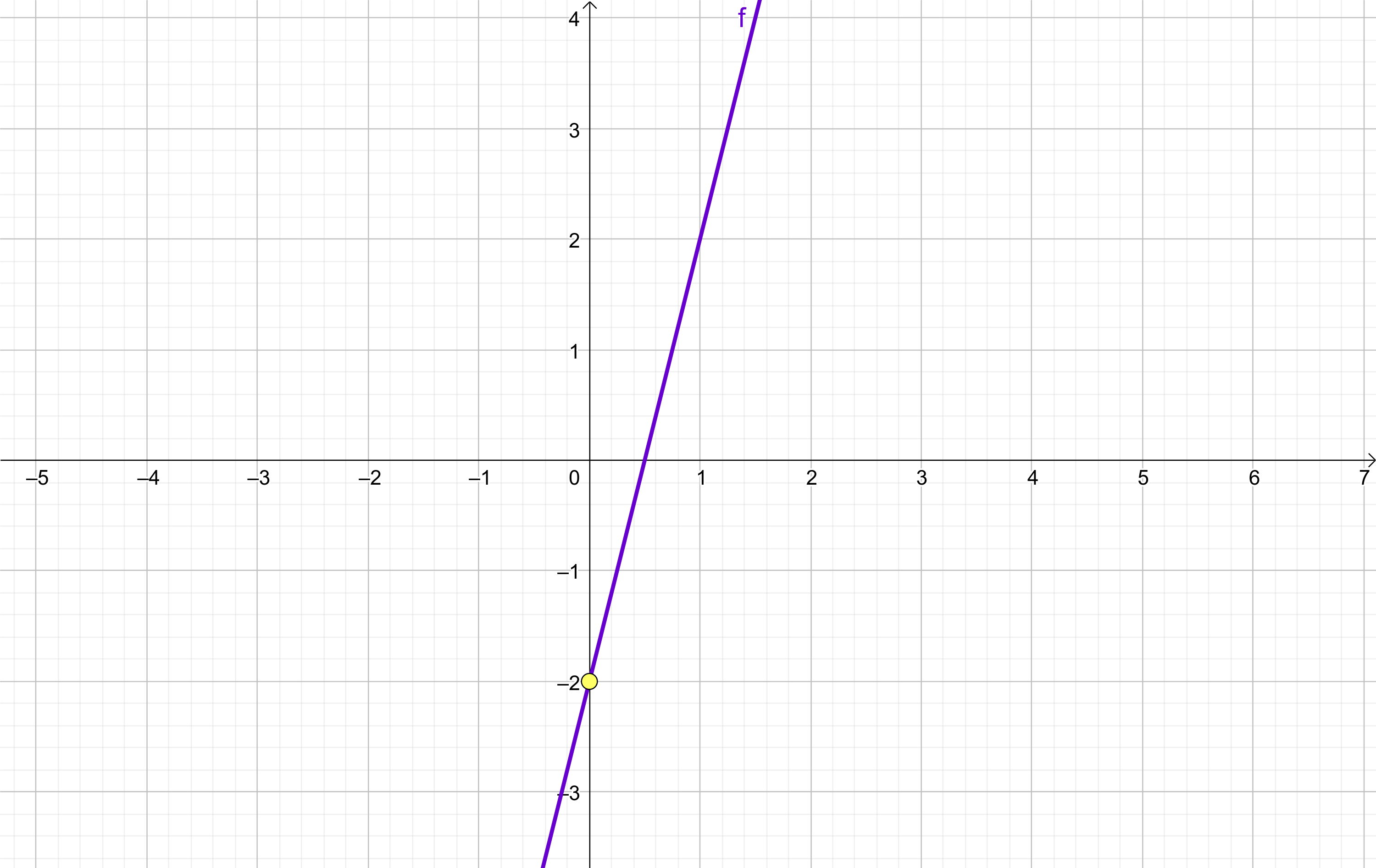La ordenada en el origen es el punto en el que la recta corta al eje vertical.
En este ejemplo ese corte de la recta con el eje vertical se produce a la altura -2
Por tanto el valor de la ordenada en el origen es -2.
Un punto más
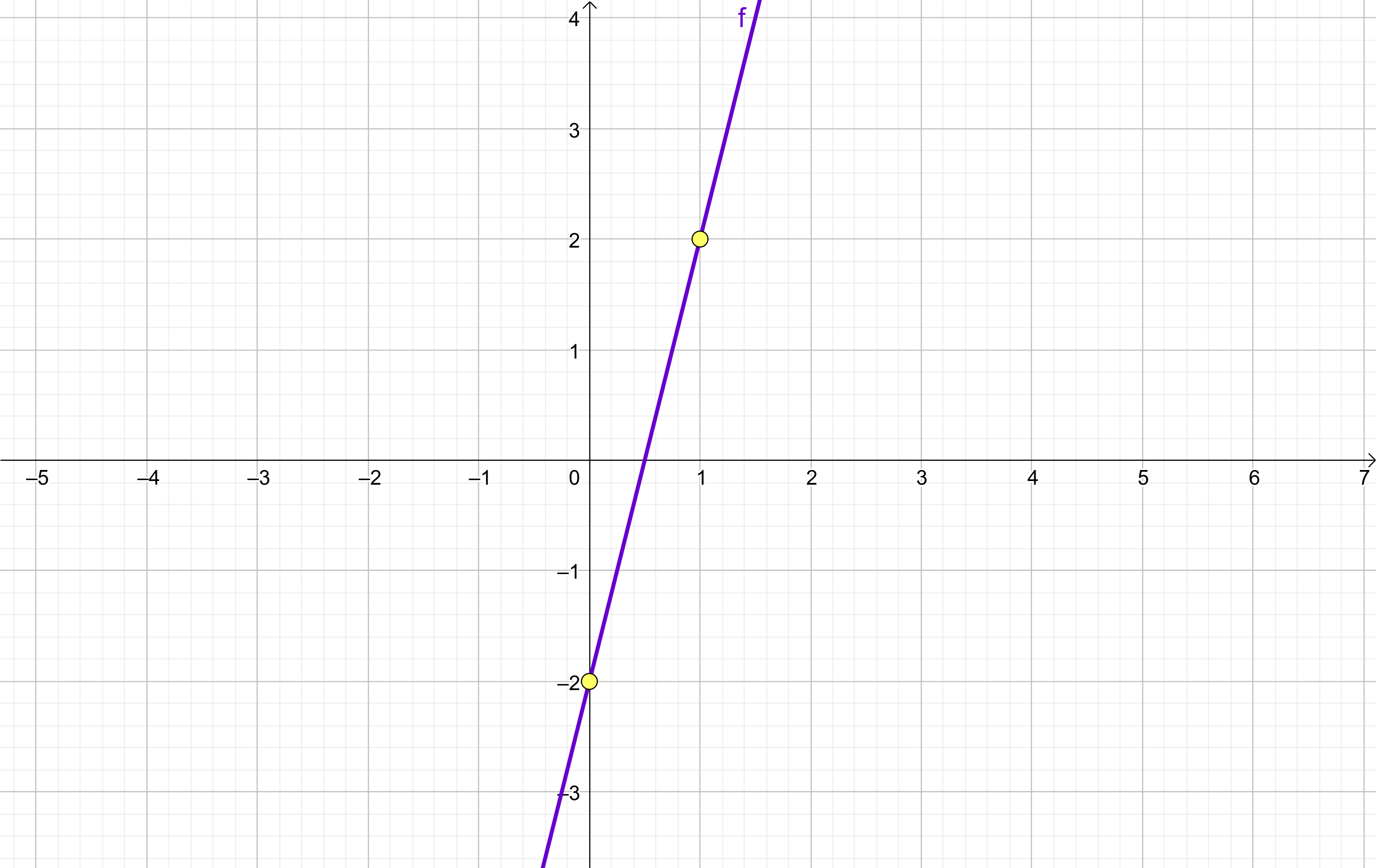Ahora marcamos un nuevo punto sobre la gráfica.
Observa que el nuevo punto está buscado de forma que su puedan determinar con exactitud sus coordenadas.
En esté ejemplo hemos encontrado que el punto (1,2) está en la gráfica.
La pendiente
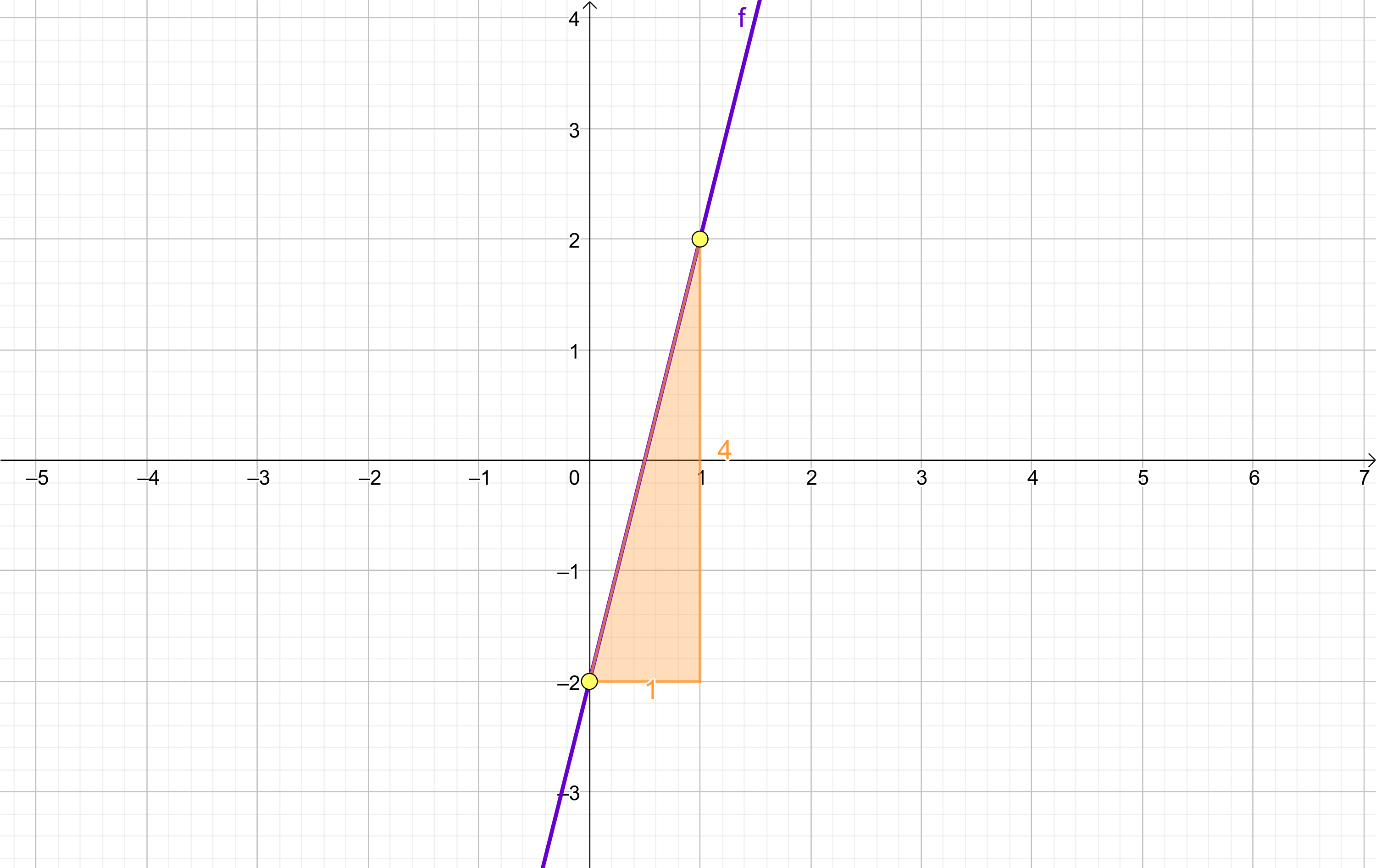Observa el triángulo rectángulo que se forma uniendo los dos puntos.
La base mide 1 unidad y la altura 4.
La pendiente se calcula con la fórmula \(pendiente\) = \( \frac{altura} {base} \) = \( \frac{4} {1} \) = \(4\)
La fórmula
La fórmula de la función afín es \(y=a⋅x+b\)
\(a\) es el valor de la pendiente y \(b\) la ordenada en el origen.
Por tanto, la expresión de la función es \(y=4⋅x-2\)
Opción B. Identifica las funciones
Lee el párrafo que aparece abajo y completa las palabras que faltan.
Opción C. Recta que pasa por dos puntos
Lee el párrafo que aparece abajo y completa las palabras que faltan.
Opción D. Codifica una función
Pulsa la bandera verde en la imagen inferior para que el programa te haga cálculos con una función afín
Veamos su código
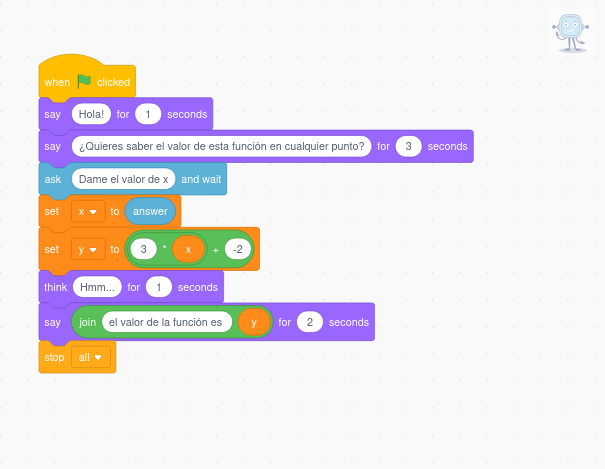
El código del programa es muy simple
Observa que
- En la instrucción azul se pide un valor por el teclado
- En las naranjas trabaja con las dos variables
- x es la entrada del teclado (answer)
- y es el cálculo de de la función afín
Modifica el código
¿Serías capaz de modificar el código para que hiciera los cálculos sobre la función afín de la izquierda?
El programa está compartido con cualquier usuario de scratch en el siguiente enlace.
Para acceder a él debes tener una cuenta en scratch. Si todavía no la tienes, recuerda que puedes crearla en la web de scratch
Cuando hagas los cambios comparte el trabajo con tus compañeros.
¿Lo usamos en el proyecto sobre los medicamentos?
Podrías modificar el programa para que ayudara a las familias a administrar el medicamento en función del peso de la persona. En ese caso, ¿en qué unidades deberían aparecer las dos variables?. ¿Serías capaz de crear un código QR que enlazara con programa de ayuda para administrar el medicamento? ¿Podría dar más información relevante el personaje de tu programa?
Motus dice ¿Cómo te has sentido?
A veces nos pueden surgir dudas cuando nos enfrentamos a una actividad nueva.
Pero estas dudas las podemos vencer. Para ello te voy a dar unos consejos:
1. Hay cosas que haces muy bien por lo que tienes que usarlas.
2. Las cosas que no salen tan bien hay que intentarlas. Para ello es muy importante que creas en ti mismo. Seguro que te sorprende lo que puedes conseguir.
3. Hay cosas que son muy difíciles. Fíjate en algún ejemplo, pregunta a tu compañero o compañera. Pide ayuda a tu profe.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0