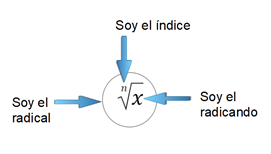
Sin embargo, no ponemos tantos problemas para multiplicarnos o dividirnos entre nosotros. Por ejemplo:
Ejemplo 1:
\sqrt[4]{4} \cdot \sqrt[4]{8}\ =\ \sqrt[4]{4 \cdot 8}\ =\ \sqrt[4]{32}\ =\ 2\sqrt[4]{2}
Ejemplo 2:
\sqrt[5]{12} \div \sqrt[5]{8}\ =\ \sqrt[5]{\frac{12}{8}}\ =\ \sqrt[5]{\frac{3}{2}}
Observa que siempre hemos de simplificar. En la multiplicación hemos sacado factores y en la división hemos simplificado la raíz.
¿Qué pasa?¿Por qué pones esa cara de incrédulo?
Vaaaale, es verdad. Hemos multiplicado y dividido raíces del mismo índice. Pero, efectivamente, no todos los casos son tan sencillos.
Te explicaré el caso más laborioso (aunque no difícil).
De nada, es un placer. Atento a este ejemplo en el que los índices de las raíces no son iguales:
\( \Large\frac{\sqrt[3]{6} \cdot \sqrt{3 \cdot 2^2}}{\sqrt[4]{18}} \ = \)
- Paso 1
-
Calcula el mínimo común múltiplo de los índices. En este caso:
\(m.c.m.\ (3,2,4)\ =\ 12 \)
- Paso 2
-
\( \Large \frac{\sqrt[12]{6^4} \cdot \sqrt[12]{3^6 (\cdot 2^2)^6}}{\sqrt[12]{18^3}} \ = \)
El índice de las raíces pasa a ser el \( m.c.m.\) que hemos calculado.
¡Ojo! Los exponentes de los radicandos cambian. Fíjate que cada factor de los radicandos se eleva al cociente resultante de \( = \large\frac{índice\ nuevo\ (m.c.m.)}{índice\ antiguo} \)
Por ejemplo, en el caso de \( \sqrt{3 \cdot 2^2} \), queda \( \sqrt[12]{3^6 (\cdot 2^2)^6} \) porque:
\( \large \frac{índice\ nuevo\ (m.c.m.)}{índice\ antiguo} = \Large\frac{12}{2}\ \normalsize =\ 6 \)
- Paso 3
-
Factoriza los radicandos
\( \Large \frac{\sqrt[12]{(2 \cdot 3)^4} \cdot \sqrt[12]{3^6 (\cdot 2^2)^6}}{\sqrt[12]{(2\cdot3^2)^3}} \ = \)
- Paso 4
-
Sigue aplicando las propiedades de las potencias, hasta dejar los radicandos reducidos a producto de potencias de factores primos.
\( \Large \frac{\sqrt[12]{2^4 \cdot 3^4} \cdot \sqrt[12]{3^6 \cdot 2^{12}}}{\sqrt[12]{2^3 \cdot3^6}} \ = \)
- Paso 5
-
Observa que podemos multiplicar y dividir las raíces, puesto que todas tienen el mismo índice.
\( \Large \sqrt[12]{\frac{2^4 \cdot 3^4 \cdot 3^6 \cdot 2^{12}}{2^3 \cdot 3^6}} \ = \)
- Paso 6
-
Y seguimos agrupando las potencias usando sus propiedades hasta simplificar al máximo.
\( \Large \sqrt[12]{\frac{2^{16} \cdot 3^{10}}{2^3 \cdot 3^6}} \ = \ \normalsize \sqrt[12]{2^{13} \cdot 3^4} \\ = \ 2 \cdot \sqrt[12]{2\cdot 3^4} \ =\ 2 \sqrt[12]{162} \)