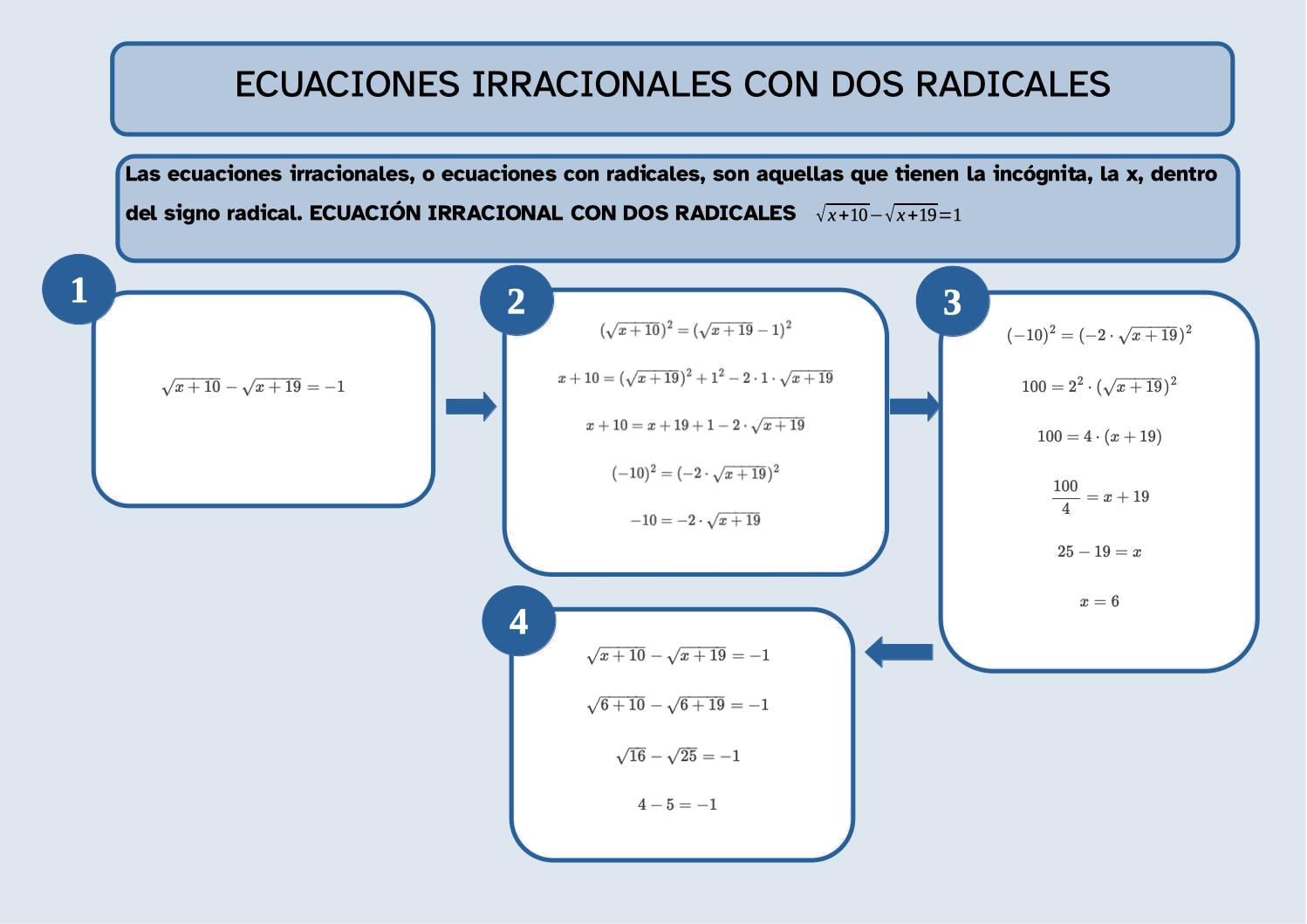
Las ecuaciones irracionales, o ecuaciones con radicales, son aquellas que tienen la incógnita, la x, dentro del signo radical.
A la hora de resolverlas, es importante seguir los pasos que te damos a continuación, tal y como hacemos con la siguiente ecuación:
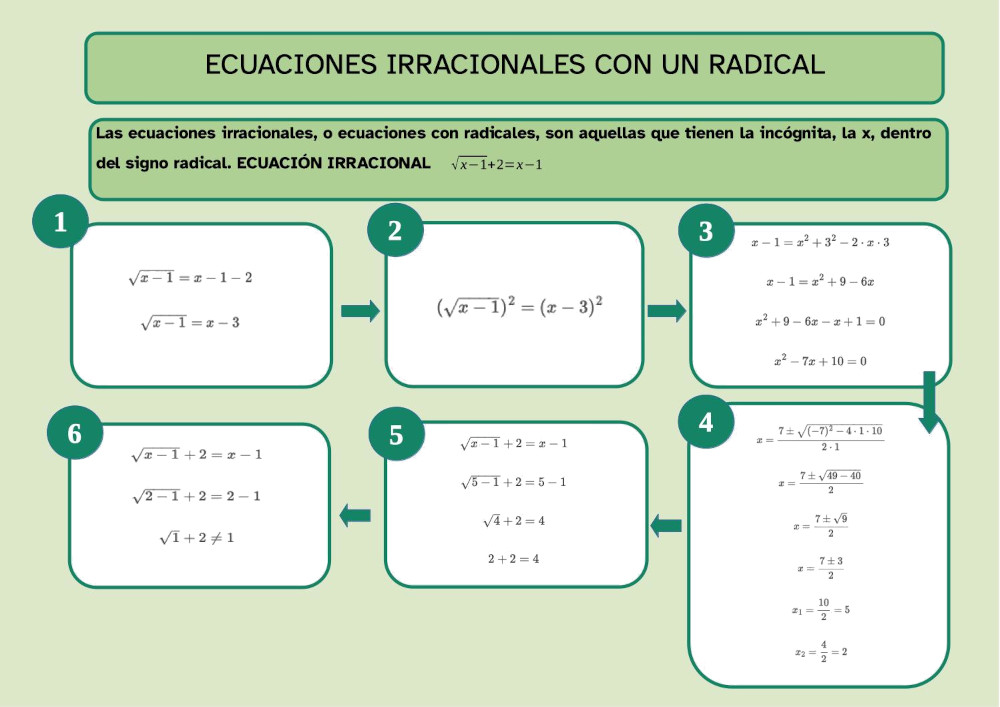
Paso 1
Dejamos el radical en uno de los dos miembros de la ecuación, pasando al otro miembro el resto de términos, y reduciendo los términos semejantes.
Paso 2
Elevamos los dos miembros de la ecuación al índice de la raíz. En nuestro caso, los elevamos a 2.
Al elevar el miembro de la izquierda al cuadrado, se elimina la raíz.
Paso 3
Realizamos las operaciones indicadas. Puede aparecernos una identidad notable, por lo que hay que recordar cómo se efectuaban éstas.
- Si es el cuadrado de la diferencia de los dos términos de un binomio, es igual al cuadrado del primer término, más cuadrado del segundo término, menos el doble producto del primer por el segundo término.
- Si es la suma de los dos términos de un binomio, es igual al cuadrado del primer término, más el cuadrado del segundo término, más el doble producto del primer por el segundo término.
x-1=x^2+3^2-2\cdot{x}\cdot{3}
Paso 4
Resolvemos la ecuación resultante.
x=\frac{7\pm{\sqrt{(-7)^2-4\cdot{1}\cdot{10}}}}{2\cdot{1}}
x=\frac{7\pm{\sqrt{49-40}}}{2}
x=\frac{7\pm{\sqrt{9}}}{2}
Paso 5
Sustituimos la solución o soluciones obtenidas en la ecuación de partida para comprobar que efectivamente son soluciones de nuestra ecuación, ya que al elevar al cuadrado los miembros de la ecuación, pueden aparecer soluciones que no sean válidas para la ecuación de partida.
Por lo tanto, el 5 sí es solución de la ecuación irracional.
Sin embargo, el 2 no es solución de la ecuación irracional.
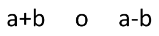 Definición:
Definición:
Expresión algebraica formada por la suma o la diferencia de dos términos o monomios.
Ejemplo:
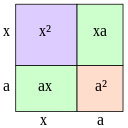
Dado el binomio \(x+7\) calcula su cuadrado
 Definición:
Definición:
Regla matemática que permite calcular de manera directa operaciones con forma polinomios.
Ejemplo:
La identidad notable más común es el cuadrado de una suma.
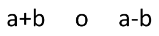



 Definición:
Definición: