Diccionario
Avanzar
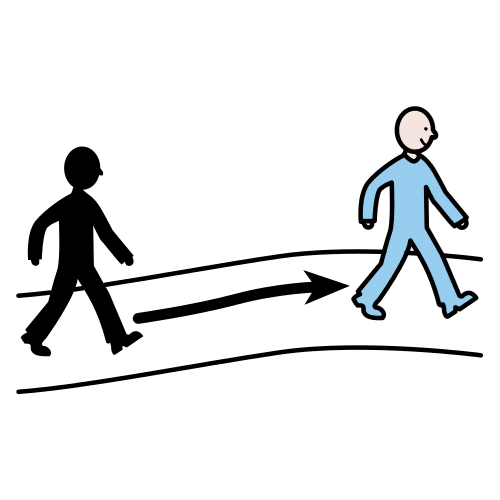
Definición:
Continuar o adelantar
Ejemplo:
En el juego debíamos avanzar lo más rápido posible
Cuestionario

Definición:
Lista de preguntas que se proponen con cualquier fin
Ejemplo:
La compañía eléctrica nos envió un cuestionario la semana pasada
Desvelar

Definición:
Descubrir algo oculto o desconocido, sacarlo a la luz
Ejemplo:
El mago no quiso desvelar el secreto de su truco
Inventar

Definición:
Descubrir algo nuevo
Ejemplo:
En clase tuvimos que inventar un instrumento que sirviese para calcular la temperatura
Potencias
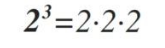
Definición:
La potencia de un número muestra cuántas veces se usa el mismo número en una multiplicación.
Ejemplo:
Las potencias son importantes para poder resolver problemas matemáticos.
Raíces
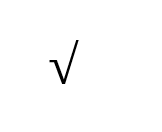
Definición:
Cantidad que se ha de multiplicar por sí misma una o más veces para obtener un número determinado.
Ejemplo:
Calcular raíces era la operación matemática que más me gustaba.
Referirnos

Definición:
Narración o explicación de algo
Ejemplo:
El mensaje que nos enviaron se refería a la excursión del próximo mes
Secretos

Definición:
Conocimiento exclusivo que alguien tiene sobre algo
Ejemplo:
Los amigos se cuentan sus secretos
Simplificada

Definición:
Hacer más fácil una cosa
Ejemplo:
Juan nos ayudó a comprender la actividad porque simplificó el vocabulario














 Una posible traducción de la inscripción podría ser:
Una posible traducción de la inscripción podría ser: