Diccionario
Incógnita
- Definición:
-
Variable que interviene en una ecuación y que es cierta para unos valores determinados; se representa normalmente con las letras x, y.
- Ejemplo:
-
La solución a la incógnita x es 29.
Crea tu propia empresa
4. Las matemáticas te ayudarán
Diccionario
Incógnita
1. Sistema de ecuaciones
¿Recuerdas cuando intentábamos averiguar el número de camisetas de cada talla que teníamos que venderle al ayuntamiento para los equipos de baloncesto?. Hay que realizar muchos cálculos y depender de la suerte para encontrar esos números.
Hay una forma mucho más sencilla de resolver este tipo de problemas.
Usaremos sistemas de ecuaciones lineales de dos incógnitas.
Presta atención porque lo que aprendas, te ayudará después a crear tu empresa,
Sistema de ecuaciones
En nuestro ejemplo, si:
Llamamos x = "Número de camisetas de la talla S"
Llamamos y = "Número de camisetas de la talla M"
y escribimos en forma de ecuaciones el enunciado, tendríamos el siguiente sistema de dos ecuaciones con dos incógnitas.
\[ \left \{
x + y = 300 \atop
4x + 5y = 2400
\right. \]
Resolver un sistema de ecuaciones
Resolver un sistema de ecuaciones consiste en encontrar los valores de las incógnitas para los cuales ambas ecuaciones son ciertas. A este par de puntos (x,y) que hacen que ambas ecuaciones sean ciertas, les llamamos solución del sistema de ecuaciones.
En nuesto ejemplo, encontramos que los valores x = 100, y = 400 son solución del sistema de ecuaciones, ya que se cumple que:
\[ \left \{
100 + 400 = 500 \atop
4·100 + 5·400 = 2400
\right. \]
Sistemas de ecuaciones equivalentes
Se dice que dos sistemas de ecuaciones son equivalentes cuando tienen la misma solución.
Los sistemas \[ \left \{
2x + 2y = 600 \atop
4x + 5y = 2400
\right. \] y \[ \left \{
x + y = 300 \atop
4x + 5y = 2400
\right. \] porque ambos tienen como solución a los valores x = 100, y = 400
Tipos de sistemas de ecuaciones
Al resolver un sistema de ecuaciones podemos encontarnos estos casos:
| Nº de soluciones | Ejemplo | Nombre |
| 1 | \[ \left \{ x + y = 300 \atop 4x + 5y = 2400 \right. \] |
Compatible determinado |
| Ninguna | \[ \left \{ x + y = 300 \atop x + y = 2400 \right. \] |
Incompatible |
| Infinitas | \[ \left \{ x + y = 300 \atop 2x + 2y = 600 \right. \] |
Compatible indeterminado |
Usar sistemas de ecuaciones te ayudará a resolver muchos problemas matemáticos. ¡¡¡Aprende un poco más sobre ellos!!!
Lectura facilitada
¿Te acuerdas como averiguaste el número de camisetas
para saber la cantidad de camisetas de talla S
y la cantidad de camisetas de la talla M tenías que vender?
Seguro que hiciste muchos cálculos.
Hay una forma más fácil de realizar esos cálculos.
Esta forma más fácil son las ecuaciones.
Sistema de ecuaciones
En nuestro ejemplo, si:
Llamamos x = "Número de camisetas de la talla S"
Llamamos y = "Número de camisetas de la talla M"
y escribimos en forma de ecuaciones el enunciado.
Tendrás el siguiente sistema de dos ecuaciones con dos incógnitas.
\[ \left \{
x + y = 300 \atop
4x + 5y = 2400
\right. \]
Resolver un sistema de ecuaciones
Para resolver un sistema de ecuaciones
Tienes que encontrar los valores de las incognitas x, y
para los cuales la ecuación es cierta.
En nuestro ejemplo, encontramos:
En nuestro ejemplo, encontramos:
los valores x = 100
los valores y = 400
son solución del sistema de ecuaciones, ya que se cumple que:
\[ \left \{
100 + 400 = 500 \atop
4·100 + 5·400 = 2400
\right. \]
Sistemas de ecuaciones equivalentes
Dos sistemas de ecuaciones son equivalentes
cuando tienen la misma solución.
Los sistemas \[ \left \{
2x + 2y = 600 \atop
4x + 5y = 2400
\right. \] y \[ \left \{
x + y = 300 \atop
4x + 5y = 2400
\right. \] porque ambos tienen como solución a los valores x = 100, y = 400
Tipos de sistemas de ecuaciones
Al resolver un sistema de ecuaciones podemos encontrarnos estos casos:
| Nº de soluciones | Ejemplo | Nombre |
| 1 | \[ \left \{ x + y = 300 \atop 4x + 5y = 2400 \right. \] |
Compatible determinado |
| Ninguna | \[ \left \{ x + y = 300 \atop x + y = 2400 \right. \] |
Incomplatible |
| Infinitas | \[ \left \{ x + y = 300 \atop 2x + 2y = 600 \right. \] |
Compatible indeterminado |
Los sistemas de ecuaciones
te ayudarán a resolver muchos problemas matemáticos.
Vamos a aprender un poco más sobre ellos.
2. Tipos de sistemas de ecuaciones
Para resolver los sistemas de ecuaciones nos encontramos con varios métodos:
Las soluciones serán las mismas, lo único que cambiará será el método que usemos para resolverlas.
Dependiendo de cada sistema de ecuaciones, nos será más fácil resolverlo por un método u otro.
Entre los métodos de solución nos encontramos:
Pasemos a ver cada uno de éstos métodos más detenidamente.
Lectura facilitada
Hay varios métodos para resolver los sistemas de ecuaciones:
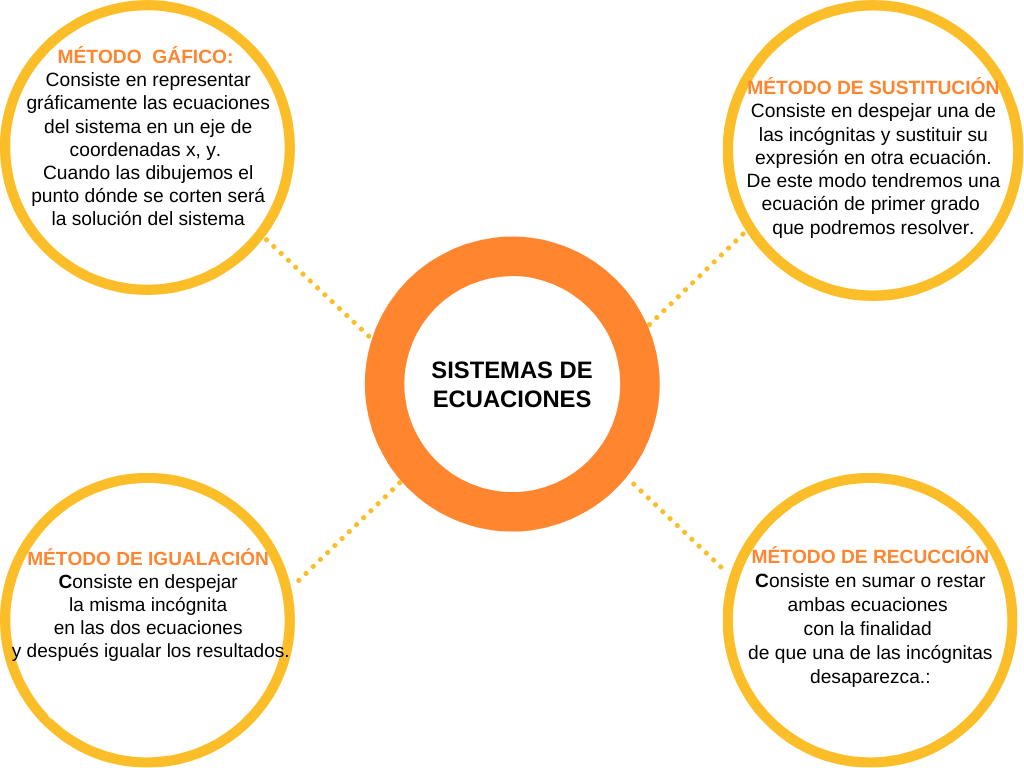
- El método gráfico: hay que representar las ecuaciones en un eje de coordenadas x, y. Cuando las dibujemos el punto dónde se corten será la solución del sistema.
- El método de sustitución: hay que despejar una de las incógnitas x o y para sustituirla en la otra ecuación. Así tendrás una ecuación de primer grado que podrás resolver.
- El método de igualación: tienes que despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.
- El método de reducción: consiste en sumar o restar las dos ecuaciones para que una de las incógnitas desaparezca.
Pasemos a ver cada uno de los métodos.
Audio
De lenguaje ordinario a lenguaje algebraico
El lenguaje algebraico nos permite expresar matemáticamente algunas expresiones del lenguaje ordinario.
Lo aplicaremos en la resolución de problemas.
Aquí tienes algunos ejemplo:
| Lenguaje ordinario/cotidiano | Lenguaje algebraico |
| María se ha gastado "x " y yo me he gastado el doble | 2x |
| Tenía pensado gastarme "x" pero me ha costado 10 euros más de lo previsto | x+10 |
| El pantalón estaba de oferta, costaba "x" pero me han descontado 3 euros | x-3 |
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0