4.4. El logotipo te hará triunfar

Diccionario

Boceto

Definición:: Borrador o esbozo de los rasgos principales de un dibujo, idea o proyecto.
Ejemplo:: El boceto de tu proyecto está quedando genial.

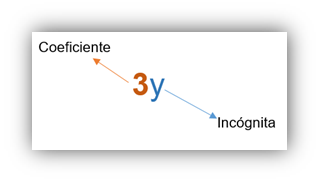
Coeficiente

Definición:: Número que se escribe a la izquierda de una variable o incógnita. Indica el número de veces que este debe multiplicarse.
Ejemplo:: En la expresión 3y, el número 8 es el coeficiente

Equivalente

Definición:: Que tiene el mismo valor.
Ejemplo:: Media hora es equivalente a dos cuartos de hora

Logotipo

Definición:: Símbolo formado por imágenes que sirve para identificar una empresa.
Ejemplo:: Se ha encargado a un diseñador el logo de nuestra empresa.

Metacrilato

Definición:: Material plástico transparente, muy rígido y resistente a los agentes atmosféricos.
Ejemplo:: La caja es de metacrilato.

Opuestos

Definición:: Enfrentado o contrario.
Ejemplo:: Hay que hacer lo opuesto para que salga bien.

Placas

Definición:: Pieza plana y delgada, generalmente de metal, en la que se graba o escribe algo.
Ejemplo:: En la puerta hay una placa con el nombre del médico.

1. El logotipo nos define

Retor dice

Recuerdas cuando hicimos prácticas en la empresa:

¿A que el logotipo era muy chulo?

Elegir un buen logotipo para tu empresa es muy importante.

Será tu carta de presentación y podrá ayudar a tu éxito.

Lectura facilitada

Cómo has visto la publicidad es muy importante.

Tienes que elegir un buen logotipo para tu empresa.

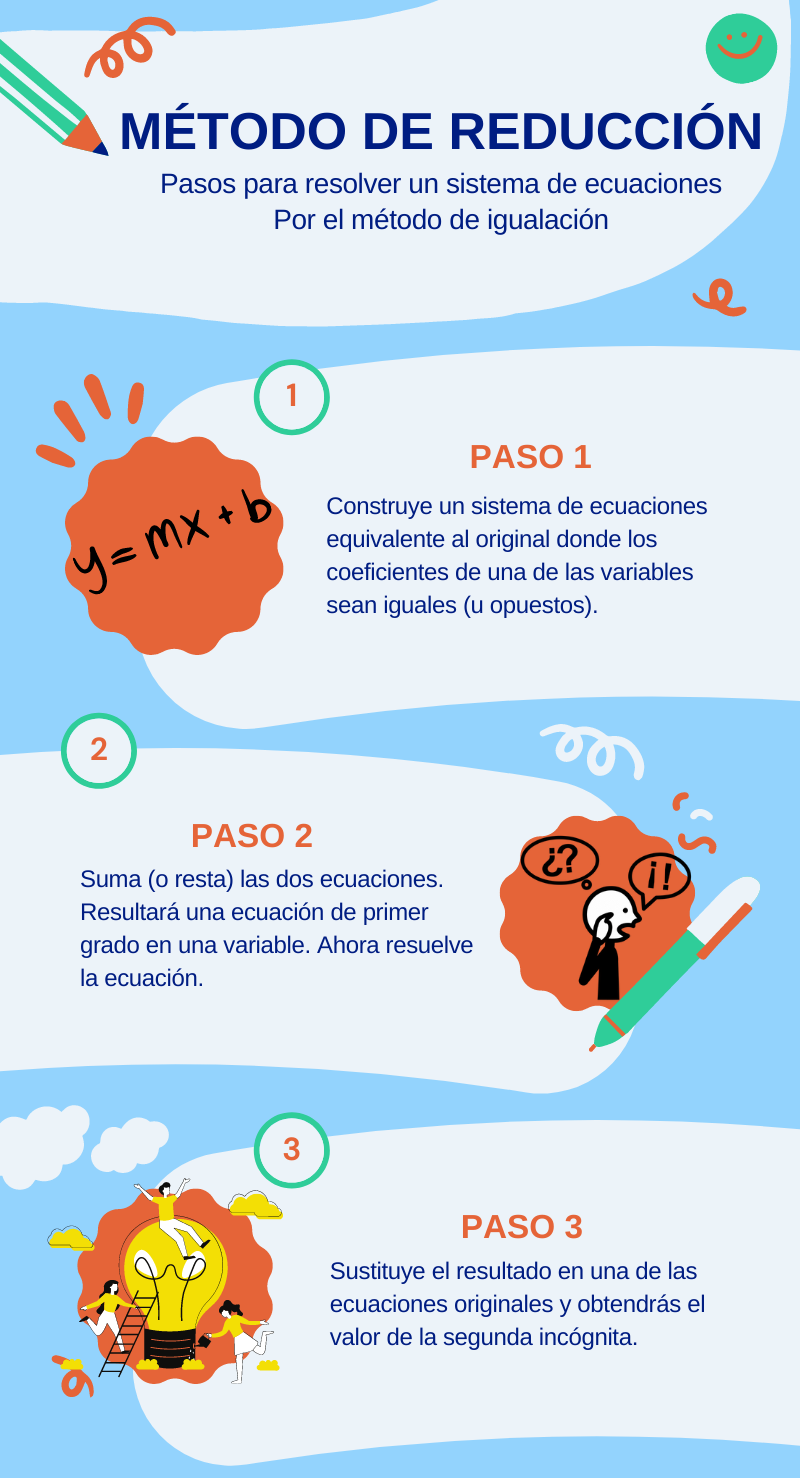
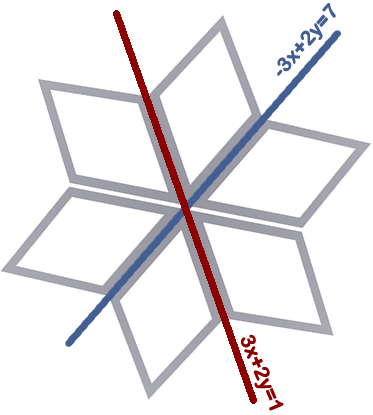
Ahora tienes que encontrar el punto central del

Logotipo de tu empresa, Deportes REA.

Lo vas a encontrar resolviendo un sistema de ecuaciones por el método de reducción.

Un buen logotipo debe...

Recuerda que un buen logotipo debe cumplir los siguientes requisitos:

Tener un diseño sencillo.
Contener solo uno o dos colores.
Tener la capacidad de ser ampliado o reducido sin perder su calidad.

2. Reducir nos ayuda

Logotipo de la empresa deportes rea Nos proponemos encontrar el punto central del logotipo de Deportes REA.

Vamos a ver cómo la resolución de sistemas de ecuaciones puede ayudarte a encontrarlo.

En este caso estudiaremos el método de reducción

Escribimos el sistema

Resolver el siguiente sistema:

\[ \left \{
x + y = 1 \atop
2x - 3y = 2
\right. \]

1. Elegimos la incógnita y conseguimos que el coeficiente de dicha variable sea el mismo o el opuesto en ambas ecuaciones.

\[ \left \{
x + y = 1 \atop
2x - 3y = 2
\right. \]

Elegimos la incógnita "x".

Para conseguir que tengan coeficientes opuestos en ambas ecuaciones, construimos un sistema de ecuaciones equivalente al original, multiplicando la primera ecuación por - 2:

\[ \left \{
- 2x - 2y = - 2 \atop
2x - 3y = 2
\right. \]

2. Sumar (o restar) ambas ecuaciones y resolver la ecuación resultante

\[ \left \{
- 2x - 2y = - 2 \atop
2x - 3y = 2
\right. \]

Al sumar ambas ecuaciones obtenemos: - 5y = 0

De donde y = 0

3. Sustituir el valor resultante en una de las ecuaciones originales y obtener el valor de la segunda incógnita.

x + y = 1

x + 0 = 1

x = 1

Luego, la solución del sistema de ecuaciones es (1,0)

Apoyo visual

¿Lo has trabajado con anterioridad? Aquí tienes una explicación más rápida

Si ya lo has trabajado con anterioridad, las siguientes imágenes te pueden ayudar:

Método de reducción

¿Cuándo me interesa resolver un sistema por el método de reducción?

Cuando tengas el mismo coeficiente en la misma incógnita en ambas ecuaciones:

Es tu turno de repasar la resolución de sistemas de ecuaciones lineales por el método de reducción.

3. Haciendo bocetos del logotipo

Vamos a encontrar el punto central del logotipo de Deportes REA.

Para ello vamos a utilizar sistemas lineales de dos ecuaciones con dos incógnitas.

Y los vamos a resolver por el método de reducción.

Opción A. Primer contacto con los logotipos

Logotipo REA
Para diseñar este logotipo en Geogebra podemos localizar el centro de la imagen conociendo el punto de corte de las dos rectas que se muestran en la siguiente imagen:

Logotipo con corte de rectas

Para ello vamos a resolver el sistema de ecuaciones por reducción:

\[ \left \{
- 3x + 2y = 7 \atop
3x + 2y = 1
\right. \]

Seguiremos los siguientes pasos:

Sumamos ambas ecuaciones

Al sumar ambas ecuaciones obtenemos: 4y = 8⇒y=2

Sustituimos en la segunda ecuación

Al sustituir en la segunda ecuación, tenemos: 3x + 4 = 1 ⇒ 3x = -3 ⇒ x = -1

¿Cuál es la solución?

Por lo que el centro del logotipo estará situado en el punto (-1,2)

¡¡Ahora te toca a ti!! Encuentra el centro del logotipo cuando las rectas sean las que se muestran en la siguiente figura:

Logotipo con corte de rectas

Opción B. Precio de los logotipos

Varios modelos de logotipo

Juan posee una empresa de diseño de logotipos en placas de metacrilato y necesita ayuda para el siguiente pedido.

Debe hacer placas de dos modelos: logotipo A y logotipo B bajo un precio total de 750 euros, teniendo en cuenta que:

Cada placa del logotipo A tiene un precio de 5 euros.
Cada placa del logotipo B tiene un precio del 10 euros.
En total debe fabricar 100 placas.

¿Cuántas placas de cada tipo debe construir?

1. Encontrar las ecuaciones que comprondrán el sistema de ecuaciones:

En primer lugar identificamos las incógnitas que formarán el sistema:

x= número de placas del logotipo A

y = número de placas del logotipo B

2. Formar las ecuaciones

x + y = Rellenar huecos (1): JXUwMDY5JXUwMDAxJXUwMDAw
Rellenar huecos (2): JXUwMDZk x + Rellenar huecos (3): JXUwMDY5JXUwMDAx y = Rellenar huecos (4): JXUwMDZmJXUwMDAyJXUwMDA1

3. Construir un sistema de ecuaciones equivalente al original donde la primera incógnita tenga coeficientes opuestos:

Rellenar huecos (5): JXUwMDc1JXUwMDE4 x + Rellenar huecos (6): JXUwMDc1JXUwMDE4 y = Rellenar huecos (7): JXUwMDc1JXUwMDE4JXUwMDA1JXUwMDAw
Rellenar huecos (8): JXUwMDZk x + Rellenar huecos (9): JXUwMDY5JXUwMDAx y = Rellenar huecos (10): JXUwMDZmJXUwMDAyJXUwMDA1

4. Sumar ambas ecuaciones y encontrar el número de placas del logotipo B que debe construir:

Rellenar huecos (11): JXUwMDZk y = Rellenar huecos (12): JXUwMDZhJXUwMDA3JXUwMDA1

y = Rellenar huecos (13): JXUwMDZkJXUwMDA1

5. Encontrar el número de placas del logotipo A que debe construir

x = Rellenar huecos (14): JXUwMDZkJXUwMDA1

6. Explicar el resultado

Necesitará construir 50 placas de cada tipo

Habilitar JavaScript

Opción C. Pierde el miedo a los cálculos

Ejemplo de logotipo
Para diseñar logotipos, es muy útil saber calcular el punto de corte de dos rectas. Practica cómo hacerlo utilizando el método de reducción:

https://www.geogebra.org/m/aDggwZT3 (Ventana nueva)

Opción D. Crea el logotipo de tu empresa

Diseña el logotipo de tu empresa, cumpliendo los siguientes requisitos:

Tener un diseño simple.
Utilizar máximo tres colores.
Sea necesario encontrar el punto de corte de dos rectas (incluye en tu trabajo la resolución de dicho sistema de ecuaciones por el método de reducción).

Pide a tu profesor/a que realice un concurso en clase con todos los logotipos que hayáis elaborado.

El logotipo que define tu empresa

Un buen logotipo puede llevar a tu empresa al éxito, por lo que su diseño debe ser muy meditado.

En esta ocasión has aprendido cómo utilizar el método de reducción en problemas relacionados con los logotipos.

Los pasos a seguir para resolver un sistema por el método de reducción son:

Construir un sistema equivalente al original donde los coeficientes de una de las variables sean iguales (u opuestos).
Sumar (o restar) ambas ecuaciones. Resultará una ecuación de primer grado en una variable. Resolver.
Sustituir el valor resultante en una de las ecuaciones originales y obtener el valor de la segunda incógnita.

4. Reviso lo aprendido

Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido)

Recuerda:

• Pregunta a tu profesor o profesora si la rellenarás en papel o en el ordenador.

• Si la rellenas en el ordenador, ¡no te olvides de guardarla en tu ordenador cuando la termines!

¡Ánimo, que lo harás genial!

Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0