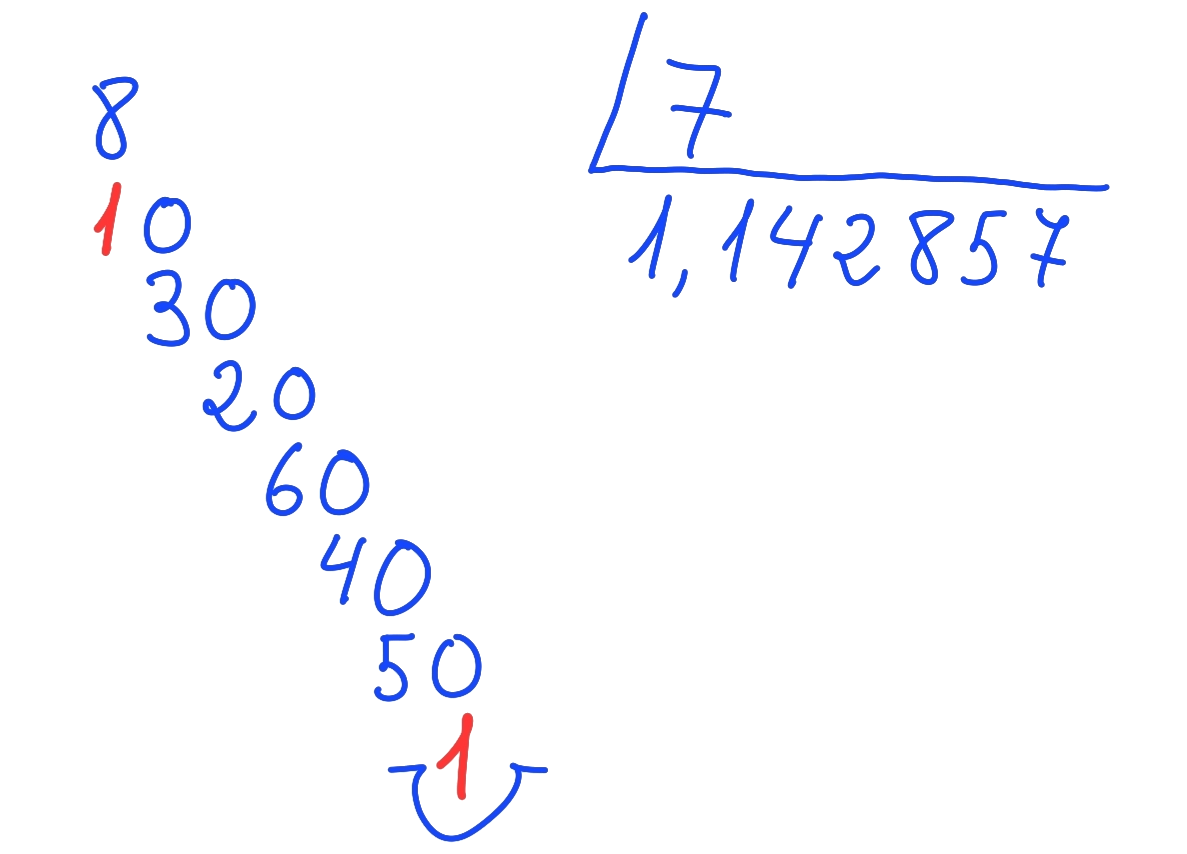Números: naturales, enteros, racionales, decimales, irracionales, reales.
¿Reconoces todos estos tipos de números? Seguro que sí.
En tu trabajo van a aparecer un montón de números (cantidades, precios, …)
¿de qué tipo son?
Para ayudarte a reconocerlos vamos a comenzar viendo cómo se definen, sus relaciones y cómo escribir un número de varias formas, esto es fundamental para realizar tu trabajo de forma correcta.
Los conjuntos numéricos son:
Los números naturales son 0, 1, 2, 3,4, 5, 6, 7, 8, 9, 10, 11, ...
El conjunto de los números naturales se nota con el símbolo $\mathbb{N} $,
que es una n mayúscula con el trazo diagonal doble.
Los números naturales son los primeros que utilizó el ser humano, y sirven para contar y para ordenar.
¿El 0 es un número natural?
Pues sobre esto no hay acuerdo.
Si usamos los números naturales para contar, es evidente que 0 debe ser un número natural.
Pero si usamos los números naturales para ordenar no tiene mucho sentido usar el 0,
pues para referirnos al primero empleamos el 1.
Los números enteros son el cero, los demás naturales con un signo + delante y con un signo - menos delante.
Los números que llevan un + delante se llaman positivos y normalmente no se pone el signo +.
Los números que llevan un - delante se llaman negativos.
El conjunto de los números enteros se nota con el símbolo $\mathbb{Z} $,
que es una z mayúscula con el trazo diagonal doble.
$\mathbb{Z}=\{...,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...\}$
Todos los números naturales son números enteros.
Los números enteros se utilizan para expresar magnitudes que toman valores mayores y menores que la cantidad de referencia que es el cero.
Por ejemplo, se usan los números enteros para expresar la temperatura,
se usan los valores positivos para las temperaturas mayores que 0º y las negativas para las temperaturas menores.
Los números enteros sirven para resolver uno de los problemas que presentan los números naturales,
y es que dos números enteros se pueden restar siempre. En los naturales sólo se puede restar un número más pequeño.
Los números racionales son los que se pueden escribir en forma de fracción. Por ejemplo: $\dfrac{3}{5} \ , \ \dfrac{-7}{3}$ .
El conjunto de los números racionales se nota con el símbolo $\mathbb{Q}$,
que es una q mayúscula con trazos dobles, o con una línea inclinada.
Todos los números enteros son números racionales,
pues basta con escribirlos mediante una fracción de denominador 1.
Los números racionales sirven para resolver uno de los problemas que tienen los números enteros,
y es que dos números racionales se pueden dividir siempre.
Todos los números racionales se pueden expresar como números decimales.
Los números irracionales son los números que no se pueden escribir en forma de fracción.
Por ejemplo: $\pi$ y $\sqrt{2}$.
Los números irracionales se pueden expresar como números decimales que tienen infinitas cifras decimales que no siguen ningún orden.
Por ejemplo, el valor de $\sqrt{2}$ con las primeras 30 cifras decimales es: 1.414213562373095048801688724209
El conjunto de los números reales es el que forma la unión de los números racionales y los números irracionales.
El conjunto de los números reales se nota con el símbolo $\mathbb{R}$, que es una r mayúscula con los trazos dobles o solo el trazo vertical doble.
Los números reales se identifican con los puntos de una línea recta.
Todos los demás conjuntos numéricos están contenidos en los números reales.
Todos los números reales se pueden expresar como números decimales.
Los números decimales están formados por una parte entera y una parte decimal separadas por una coma o punto decimal.
La parte entera la forman las cifras que hay a la izquierda de la coma y se corresponde a un número entero. La parte decimal es la que hay a la derecha de la coma, y el valor de cada cifra es la décima parte de la cifra de su izquierda.
Los números decimales se clasifican según sus cifras decimales.
Los números decimales exactos son los que tienen un número finito de cifras decimales.
Es decir, las cifras decimales se acaban.
Ejemplos:
4.758 -321.8991 0.6
Los números enteros son números decimales que su parte decimal es cero: 5=5.0
Todos los números decimales exactos son números racionales.
Los números decimales periódicos son los que tienen infinitas cifras decimales,
que se repiten en el mismo orden.
El conjunto de cifras decimales que se repite se llama periodo,
y se le pone un arco encima para señalarlo.
Por ejemplo:
$2.3535353535353535353535... =2.\widehat{35}$. En este número decimal el periodo es 35 que se repite infinitas veces.
Hay dos tipos de números decimales periódicos:
Ejemplos: $0.\widehat{3}$, $23.\widehat{823}$
el conjunto de estas cifras que están entre la coma decimal y el periodo se llama anteperiodo.
Ejemplos: $1.3\widehat{4}=1.344444444...$, $0.45\widehat{321}=0.45321321321...$
Todos los números decimales periódicos son números racionales.
Los números decimales irracionales son los números decimales que tienen infinitas cifras decimales que no siguen ningún orden de repetición.
Los números decimales irracionales son los números irracionales.
Ejemplos:
0.1010010001000100001...,
$\sqrt{2}=$1.414213562373095048801688724209...,
$\pi =$3.14159265358979323846264...
{"id":"b6195de7-fbdf-42a1-bebd-2880b5b0127d","title":"Números decimales","mindmap":{"root":{"id":"c32be1c5-0074-4ca1-b223-3fccfce5b8eb","parentId":null,"text":{"caption":"Números decimales","font":{"style":"normal","weight":"bold","decoration":"none","size":20,"color":"#000000"}},"offset":{"x":0,"y":0},"foldChildren":false,"branchColor":"#000000","children":[{"id":"bff59d07-b6b8-4fcb-9a9a-8601bd64f9aa","parentId":"c32be1c5-0074-4ca1-b223-3fccfce5b8eb","text":{"caption":"Exáctos","font":{"style":"normal","weight":"normal","decoration":"none","size":23,"color":"#000000"}},"offset":{"x":212,"y":-129.00001525878906},"foldChildren":false,"branchColor":"#bd1d76","children":[]},{"id":"61bb58ad-072d-40ab-ab9f-76c4ed8faa63","parentId":"c32be1c5-0074-4ca1-b223-3fccfce5b8eb","text":{"caption":"Periódicos","font":{"style":"normal","weight":"normal","decoration":"none","size":23,"color":"#000000"}},"offset":{"x":197,"y":-12},"foldChildren":false,"branchColor":"#413706","children":[{"id":"c2950fd5-0817-4989-a52f-8524bbcebce3","parentId":"61bb58ad-072d-40ab-ab9f-76c4ed8faa63","text":{"caption":"Puros","font":{"style":"normal","weight":"normal","decoration":"none","size":19,"color":"#000000"}},"offset":{"x":185,"y":-72.99998474121094},"foldChildren":false,"branchColor":"#413706","children":[]},{"id":"71b9d0e4-aa5d-4c0f-b8a5-dcbd2d6b0c99","parentId":"61bb58ad-072d-40ab-ab9f-76c4ed8faa63","text":{"caption":"Mixtos","font":{"style":"normal","weight":"normal","decoration":"none","size":19,"color":"#000000"}},"offset":{"x":178.23333740234375,"y":70.23330688476562},"foldChildren":false,"branchColor":"#413706","children":[]}]},{"id":"64a4524f-af1c-4947-9f1f-17f2f5909ec4","parentId":"c32be1c5-0074-4ca1-b223-3fccfce5b8eb","text":{"caption":"Irracionales","font":{"style":"normal","weight":"normal","decoration":"none","size":23,"color":"#000000"}},"offset":{"x":173,"y":145},"foldChildren":false,"branchColor":"#8747e4","children":[]}]}},"dates":{"created":1658295067165,"modified":1658295247875},"dimensions":{"x":4000,"y":2000},"autosave":false}
Todas las fracciones se pueden escribir como número decimal, exacto o periódico.
Si tienes una fracción,
¿Cuál es el número decimal que le corresponde?
Para escribir una fracción como número decimal basta con realizar la división,
hasta que salga de resto cero o se repita el resto.
A continuación tienes tres ejemplos, uno en el que sale un decimal exacto, otro un decimal periódico puro y otro con un decimal periódico mixto.
Escribe como número decimal: $\dfrac{7}{8}$
Se hace la división, hasta que salga resto cero o se repita el resto.
Como sale resto cero se acaba la división y el número decimal es el cociente: $\dfrac{7}{8}=0.875$
Escribe como número decimal: $\dfrac{8}{7}$
Se hace la división, hasta que salga resto cero o se repita el resto.
Como se repite el resto, vuelve a salir 1, el número decimal es periódico. Para determinar el periódo hay que fijarse en la cifra que aparece en el cociente después de que aparezca por primera vez el 1 en el resto. Esa cifra es el 1 del cociente, por tanto, esa es la primera cifra del periodo. Como 1 también es la primera cifra decimal el número es periódico puro.
$\dfrac{8}{7}=1.\widehat{142857}$
Escribe como número decimal: $\dfrac{5}{6}$
Se hace la división, hasta que salga resto cero o se repita el resto.
Se repite el resto, vuelve a salir 2, el número decimal es periódico. Para determinar el periodo hay que fijarse en la cifra que aparece en el cociente después de que aparezca por primera vez el 2 en el resto. Esa cifras es el 3, por tanto, la primera cifra del período es el 3, en este caso es la única cifra periódica. Como el 3 no es la primera cifra decimal el número es periódico mixto.
$\dfrac{5}{6}=0.8\widehat{3}$
A continuación tienes 3 ejemplos:
1.- El resultado es decimal exacto.
2.- El resultado es decimal periódico puro.
3.- El resultado da con un decimal periódico mixto.
Primero hay que asegurarse que la fracción es irreducible.
Después hay que realizar la factorización del denominador en producto de factores primos.
Si en la factorización los únicos números primos que aparecen son el 2 y/o el 5 el número es exacto.
Si en la factorización aparece un número primo distinto de 2 y de 5 el número es periódico.
Los únicos números decimales que se pueden expresar en forma de fracción
son los exactos y los periódicos.
El proceso para escribir un número decimal en forma de fracción cambia según el número sea exacto,
periódico puro o periódico mixto.
Vamos a explicar cada proceso usando un ejemplo.
Escribe como fracción el número 2.48
| 1º Llama $n$ al número decimal | 1º: $n=2.48$ |
| 2º Multiplica los dos miembros de la fracción por la potencia de 10 necesaria para que desaparezcan las cifras decimales |
2º: Como hay dos cifras decimales hay que multiplicar por $10^2=100$ $100n=248$ |
| 3º Se despeja $n$ | 3º: $n=\dfrac{248}{100}$ |
| 4º Se simplifica la fracción | 4º: $n=\dfrac{248}{100}=\dfrac{62}{25}$ |
Por tanto, $2.48=\dfrac{62}{25}$
Escribe como fracción el número: $3.\widehat{48}$
| 1º Llama $n$ al número decimal | 1º: $n=3.\widehat{48}$ |
| 2º Multiplica los dos miembros de la fracción por 10 elevado al número de cifras periódicas |
2º: Como hay dos cifras decimales periódicas hay que multiplicar por $10^2=100$ $100n=348.\widehat{48}$ |
| 3º A la última ecuación se le resta la primera | 3º: $\begin{array}{rr} \ & \\ \ & 100n=348.\widehat{48}\\- & n=3.\widehat{48}\\ \hline \ & 99n=345 \end{array}$ |
| 4º Se despeja $n$ | 4º: $n=\dfrac{345}{99}$ |
| 5º Se simplifica la fracción | 5º: $n=\dfrac{345}{99}=\dfrac{115}{33}$ |
Por tanto, $3.\widehat{48}=\dfrac{115}{33}$
Escribe como fracción el número: $0.27\widehat{5}$
| 1º Llama $n$ al número decimal | 1º: $n=0.27\widehat{5}$ |
| 2º Multiplica los dos miembros de la fracción por 10 elevado al número de cifras decimales que no son periódicas |
2º: Como hay dos cifras decimales no periódicas hay que multiplicar por $10^2=100$ $100n=27.\widehat{5}$ |
| 3º Multiplica los dos miembros de esta última expresión por 10 elevado al número de cifras decimales periódicas |
3º: Como sólo hay una cifra decimal no periódica se multiplica por 10 $1000n=275.\widehat{5}$ |
|
4º A la última ecuación se le resta la anterior |
3º: $\begin{array}{rr} \ & \\ \ & 1000n=275.\widehat{5}\\- & 100n=27.\widehat{5}\\ \hline \ & 900n=248 \end{array}$ |
| 5º Se despeja $n$ | 5º: $n=\dfrac{248}{900}$ |
| 6º Se simplifica la fracción | 6º: $n=\dfrac{248}{900}=\dfrac{62}{225}$ |
Por tanto, $0.27\widehat{5}=\dfrac{62}{225}$
_page-0001.jpg)
Ahora es tu turno de comprobar que identificas todos los números y los clasificas correctamente, sin olvidar, la conversión de decimales y fracciones .
Arrastra cada uno de los números sobre el tipo de decimales que es cada uno.
Practica el cálculo del número decimal que representa una fracción. Supera cinco niveles.
Practica el cálculo de la fracción generatriz de un número decimal.
No olvides que debes dar la fracción irreducible, para pasar de nivel.
Supera los cinco niveles propuestos.
Como sabes, si a un número decimal le añades ceros a la derecha el número no cambia. Por eso no tiene sentido escribir un número periódico que la parte periódica valga 0.
¿Hay alguna otra cifra que tampoco tenga sentido usar en la parte periódica?
Razona y escribe tu respuesta.
Intentar escribir el número $4.\widehat{9}$ en forma de fracción y observa qué pasa.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0