Diccionario
Conservas
Definición:
Alimentos envasados herméticamente para ser conservados durante mucho tiempo.
Ejemplo:
Mario tiene en su restaurante diferentes conservas.
Construye tu caseta de Feria
4.3 Decorar con circunferencias y sectores circulares
Ahora que has visto lo importante de algunas figuras planas y no tan planas, estás preparado para aprender a diseñar una caseta de feria un poco más especial.
En este apartado vas a aprender a trabajar con circunferencias, semicircunferencias y sectores circulares para completar el diseño de una caseta de feria.
Para poder hacerlo vas a necesitar unas herramientas de trabajo muy importantes: regla, compás y transportador de ángulos.
1. Con circunferencias, tenemos mucho que hacer
Cuando estemos diseñando nuestra caseta de feria, podemos utilizar elementos matemáticos para mejorar la decoración, organizar su montaje o para crear una maqueta.
Parece que no, pero decorar con elementos matemáticos siempre es muy llamativo. Si lo hacemos bien, puede quedar un frontal de la caseta muy bonito.
¿Qué cosas necesitamos saber? Vamos a ver algunos aspectos importantes:
La circunferencia y sus cosas
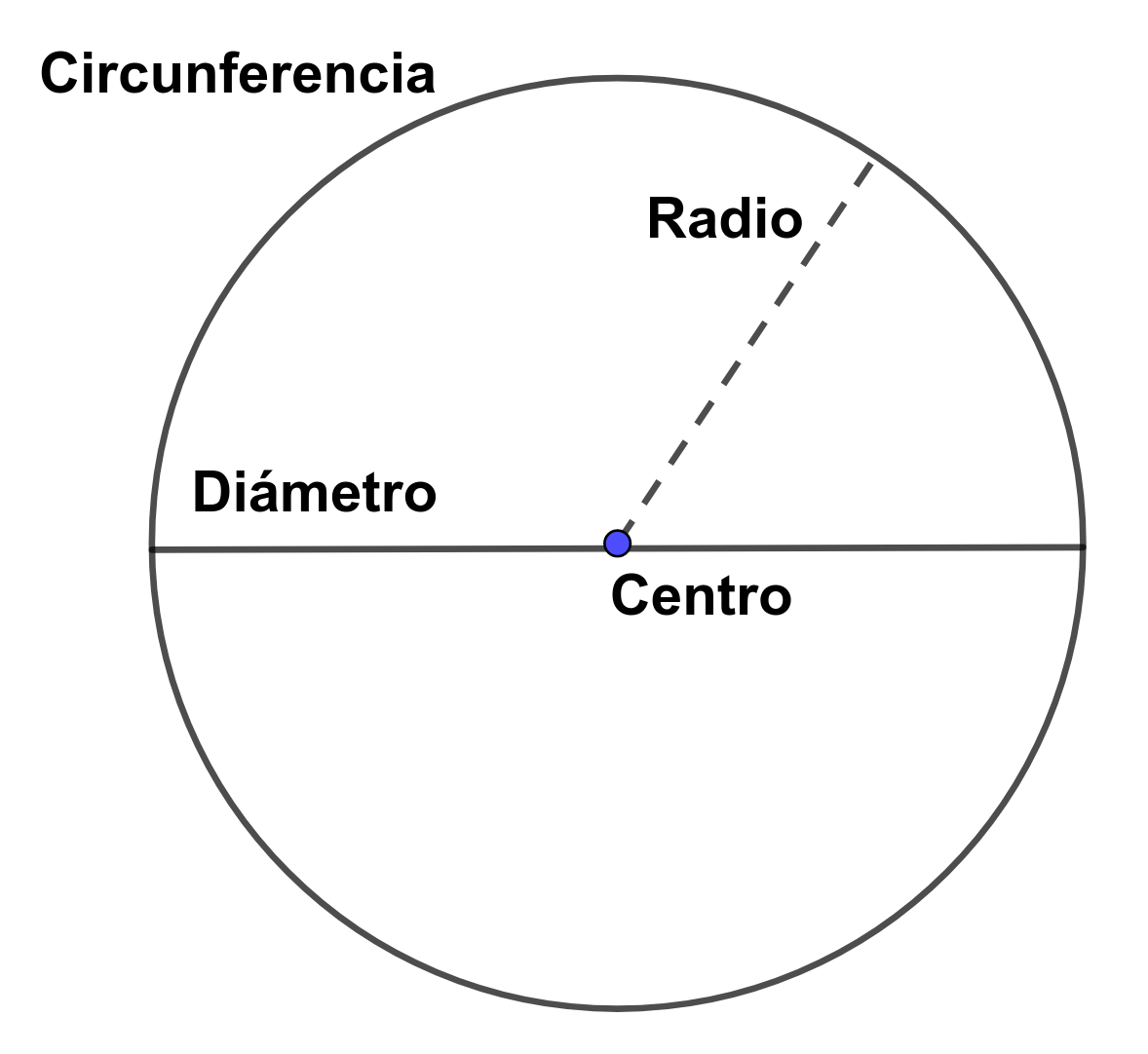
En primer lugar, es necesario saber qué es una circunferencia y qué elementos nos vas a ser útiles para trabajar en el diseño de nuestra caseta. Vamos a comenzar con algunas definiciones que nos serán de gran utilidad.
Una circunferencia es una línea plana cerrada que tiene todos sus puntos a una misma distancia de otro punto interior llamado centro.
Esa distancia a la que están todos los puntos se denomina radio.
El doble del radio es lo que denominamos como diámetro.
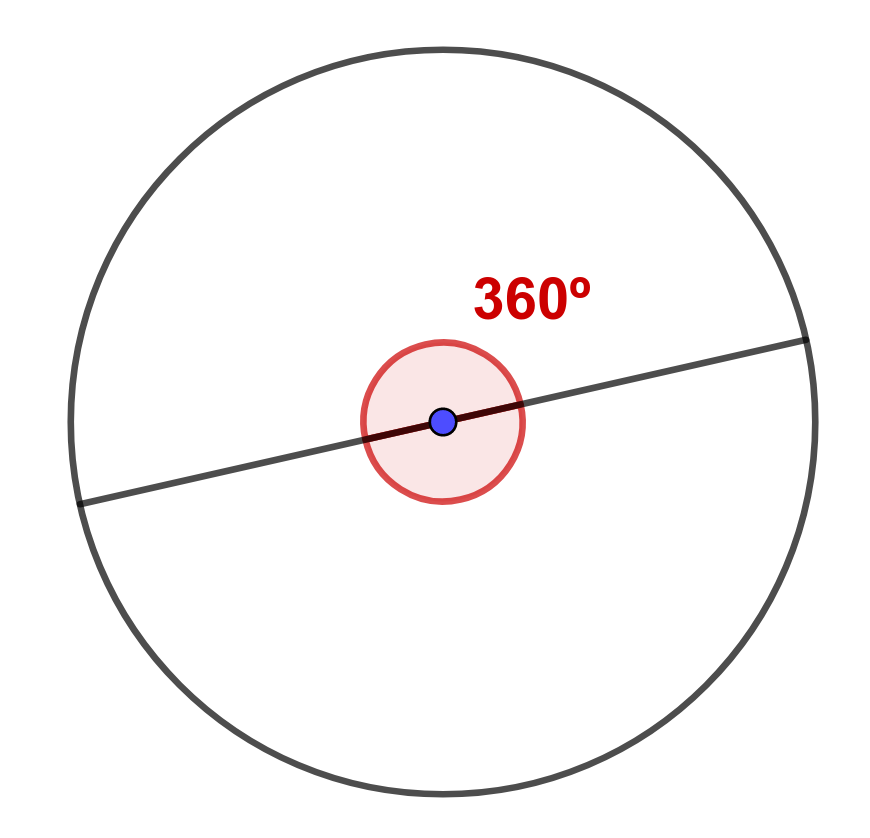
El ángulo interior de la circunferencia es de una vuelta completa, 360º.
Dentro y la curva
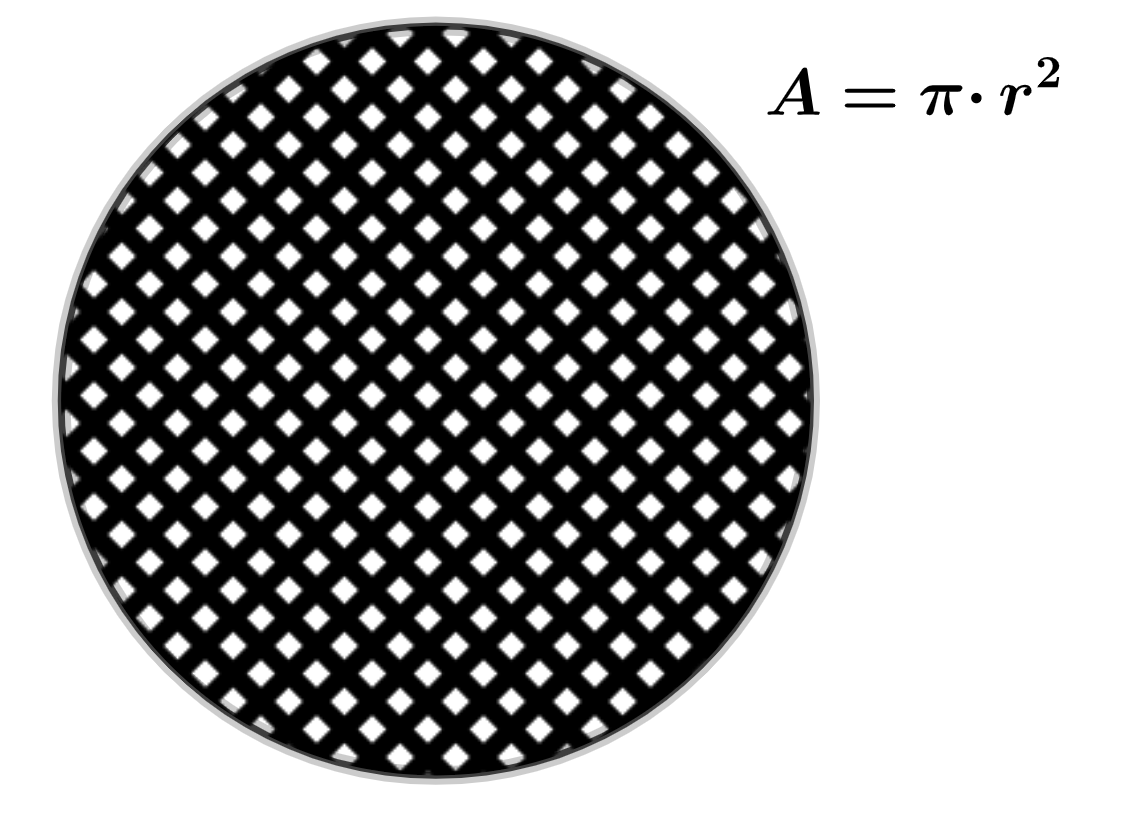
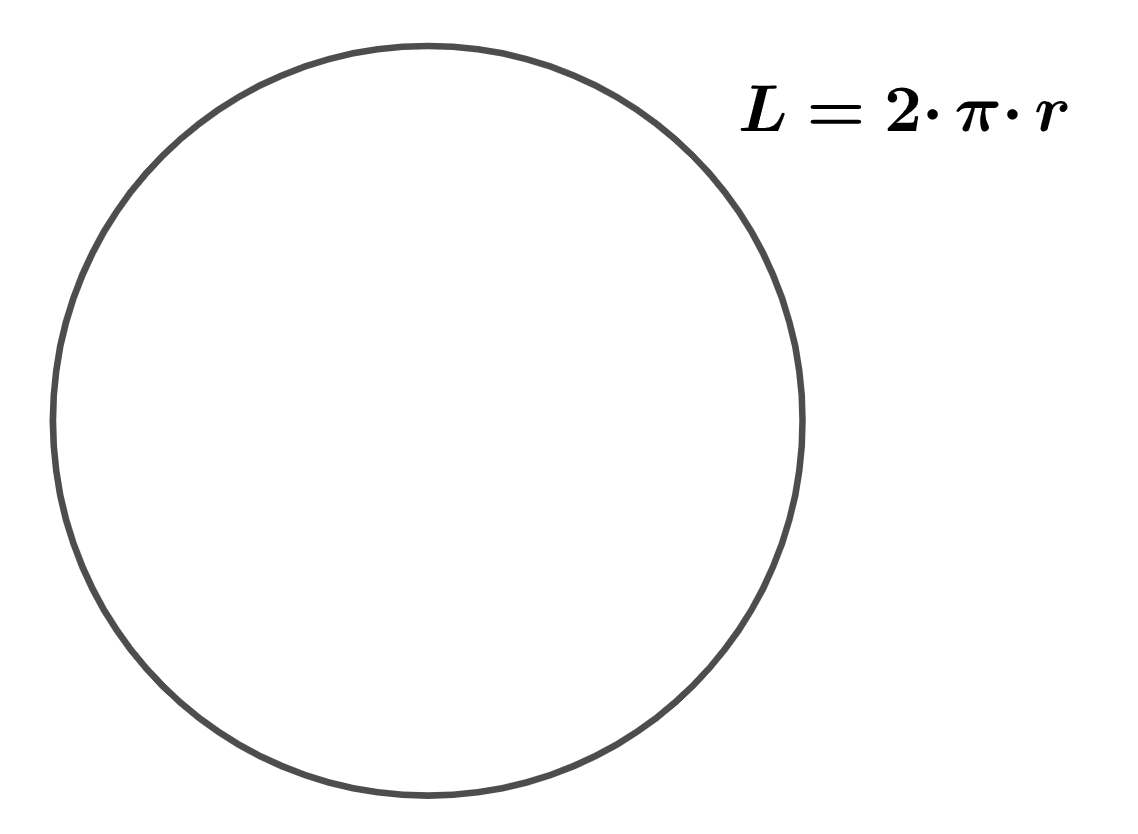
Al trabajar con una circunferencia, es interesante utilizar la zona interior a esta línea y saber cuánto mide la propia línea. Es lo que denominamos área de la circunferencia y perímetro. Nos puede ser útil para trabajar con la decoración de la portada de nuestra caseta. ¿Cómo podemos calcularlo?
El área de una circunferencia es la superficie que queda encerrada por la línea cerrada y podemos calcularla como el producto del número Pi por el radio de la circunferencia al cuadrado.
El perímetro el la longitud de la propia curva y se puede calcular como el doble del número Pi por el radio de la circunferencia.
¿Y la mitad?
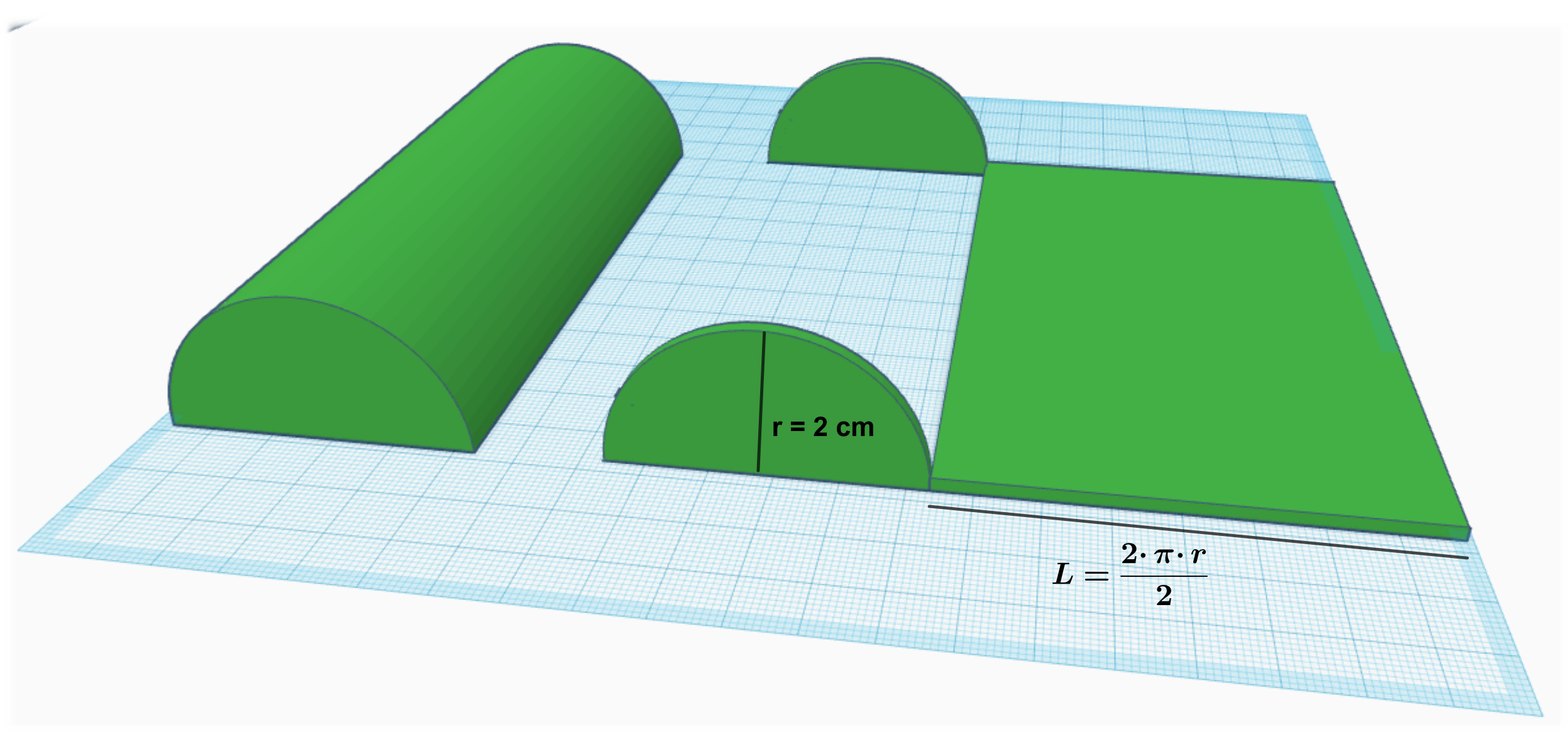
Para trabajar en la decoración de la caseta utilizando circunferencias, puede que en alguna ocasión utilicemos la mitad. A esta figura se le denomina semicircunferencia y tanto el área como el perímetro se calcula como la mitad del de la circunferencia con que tenga ese mismo radio.
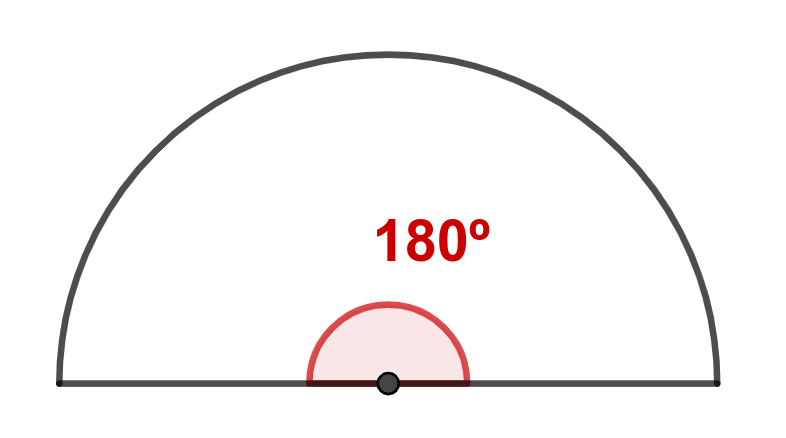
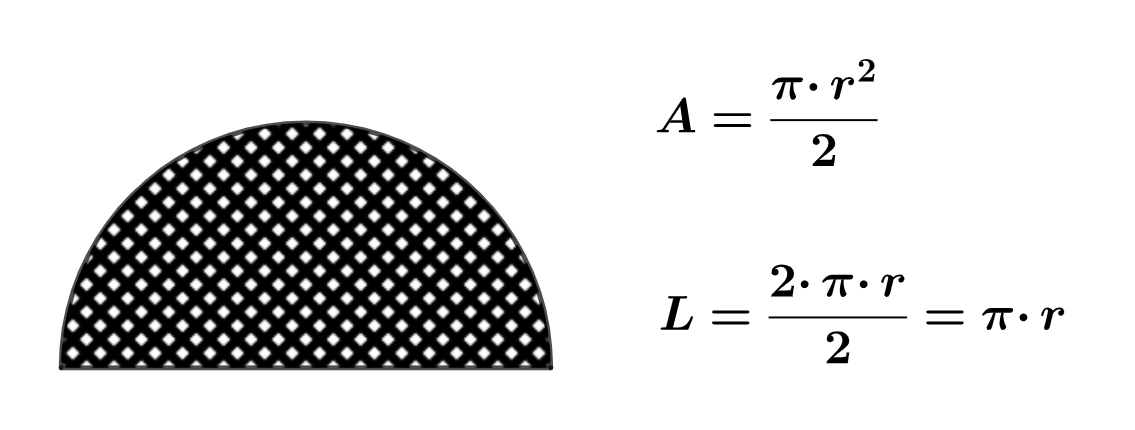El ángulo interior de una semicircunferencia es la mitad de 360º, 180º.
¿Y más pequeña?
Cada vez que queramos dividir la circunferencia en partes iguales, tanto el ángulo, el perímetro como el ángulo interior de cada parte quedará dividido por el número de partes. Por ejemplo, si quiero dividir en cuatro partes, lo dividiré entre cuatro y quedará de la siguiente manera: 
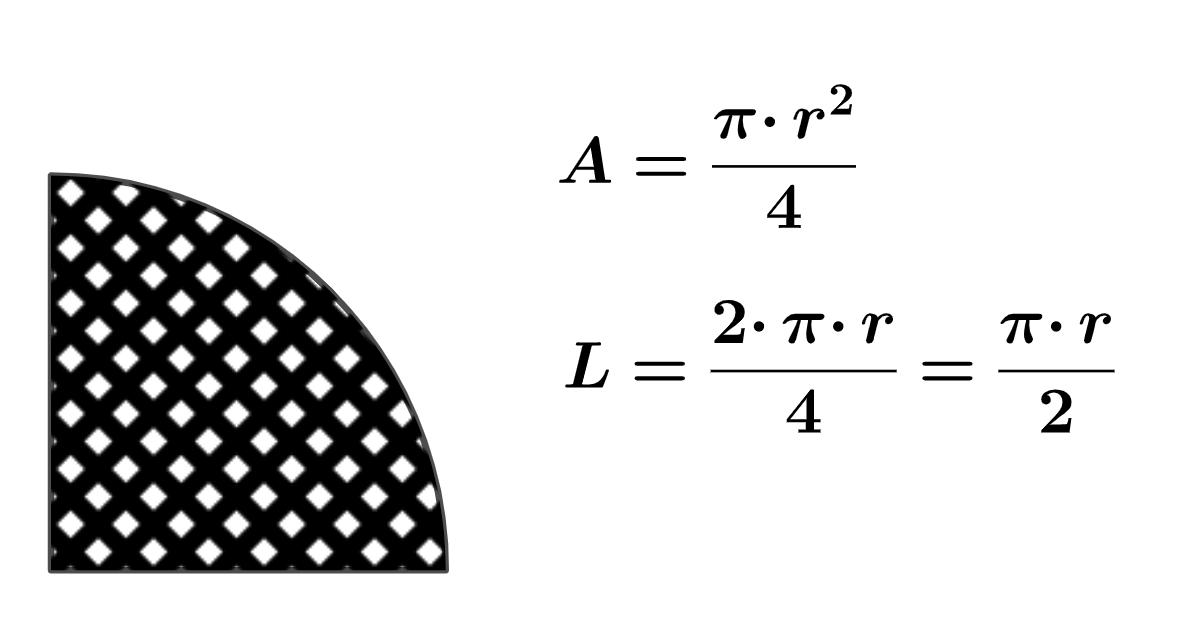
Por ejemplo, si el radio r = 3 metros, el área y el perímetro de este sector circular serían los siguientes:
A = (3'14 · 3²) : 4 = 7'1 m²
L = (3'14 · 3 ) : 2 = 4'7 m
El ángulo interior de un cuarto de circunferencia es la cuarta parte de 360º, 90º.
Una cualquiera
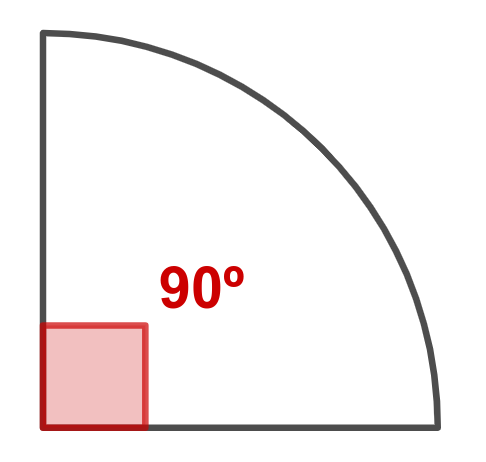
En general, se puede coger cualquier sección de la circunferencia para crear una composición artística que sirva para decorar el frontal de tu caseta. Simplemente tengo que pensar en cuántas partes se queda divida una circunferencia. Por ejemplo, para dividir la circunferencia en 8 partes iguales, quedaría de la siguiente manera
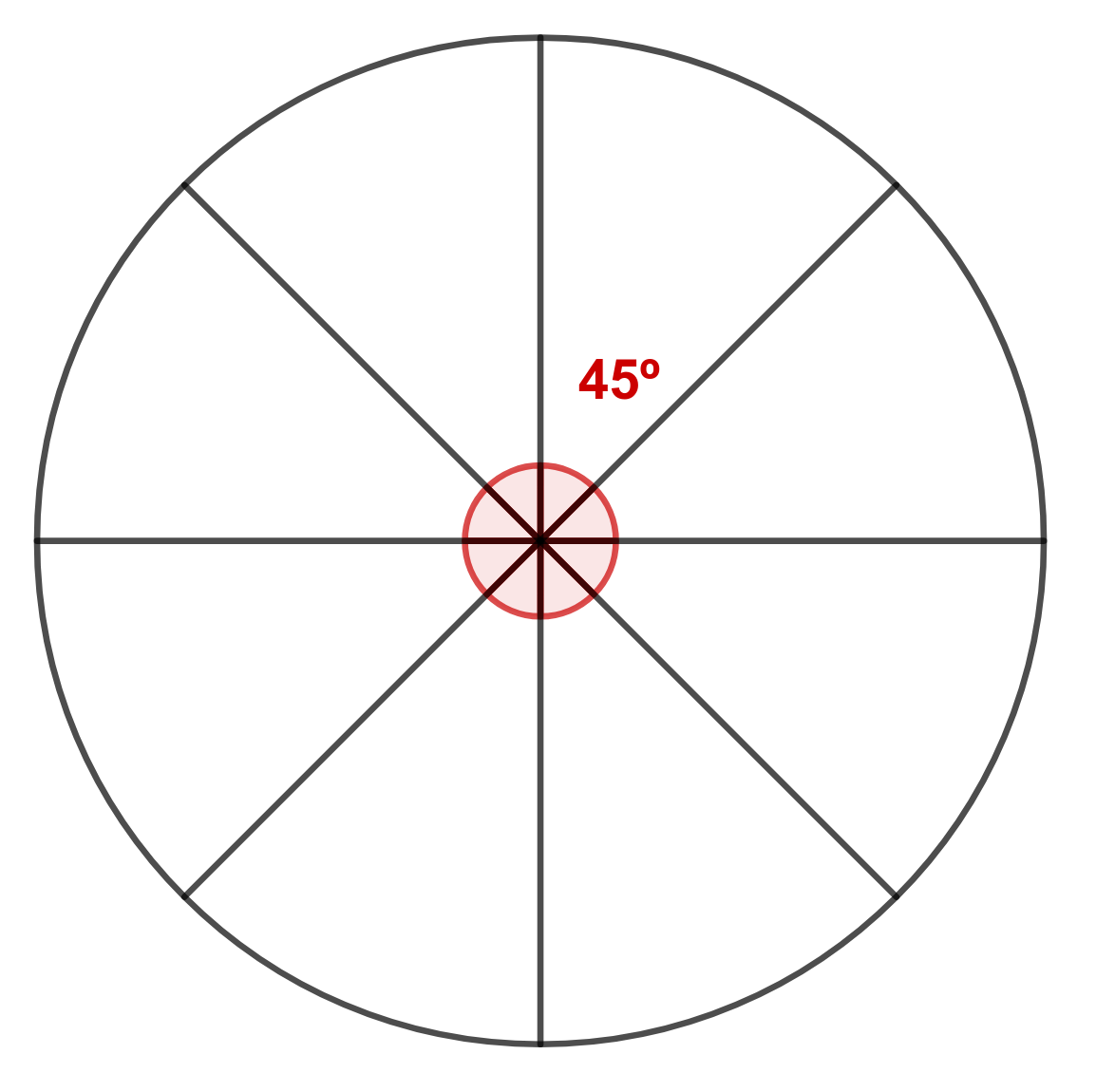
Cada sector quedará de la siguiente manera, pudiendo calcular su área y perímetro:
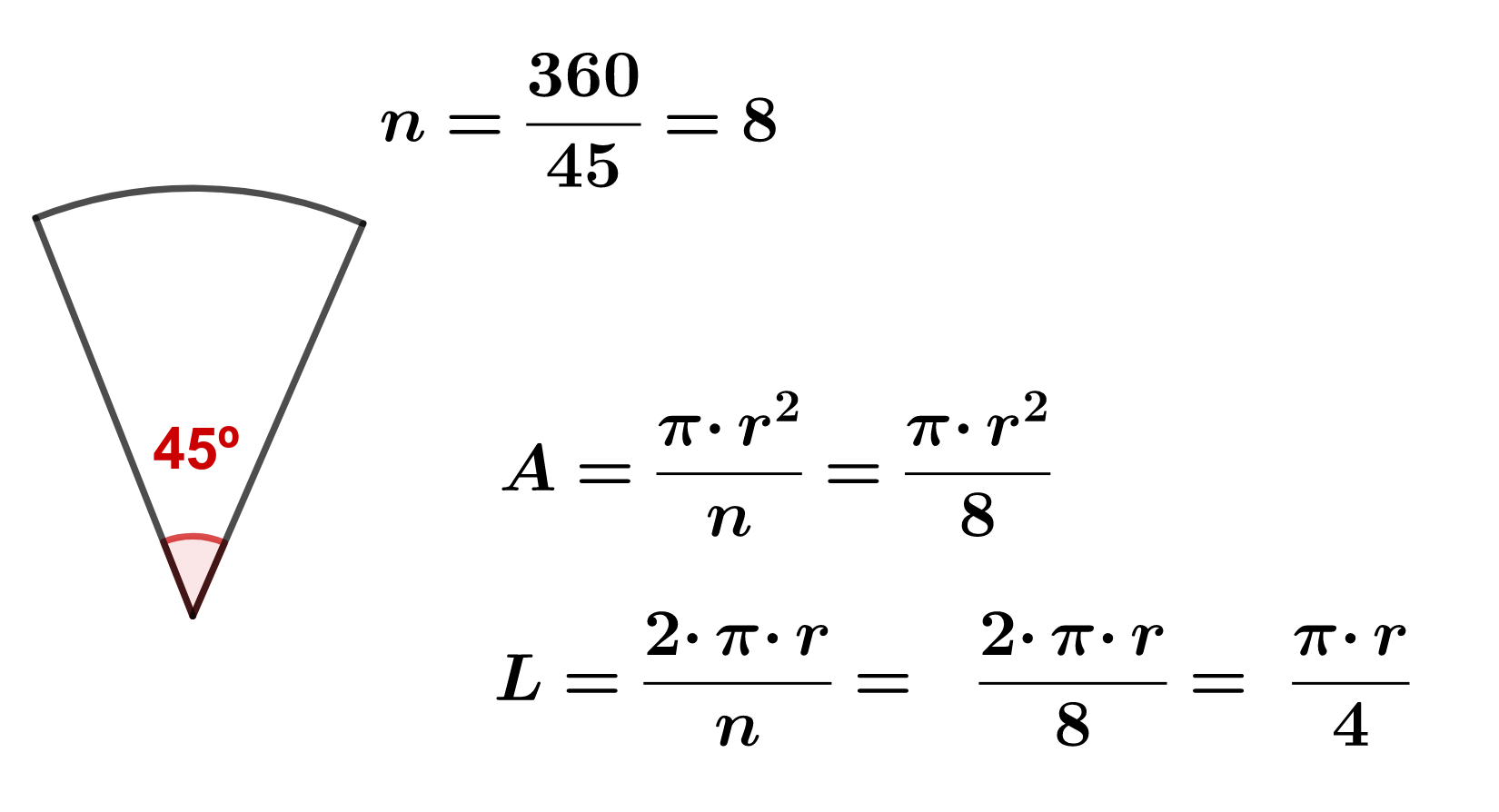Así, podemos calcular el ángulo del sector pensando en cuántos trozos queremos dividir el diseño de una circunferencia. Por ejemplo, si quiero hacer un diseño dividiendo una circunferencia en 12 partes (la semicircunferencia en 6 partes) cada sector tendrá un ángulo de 360º : 12 = 30º.
2. ¿Cómo sería la maqueta de una caseta así?
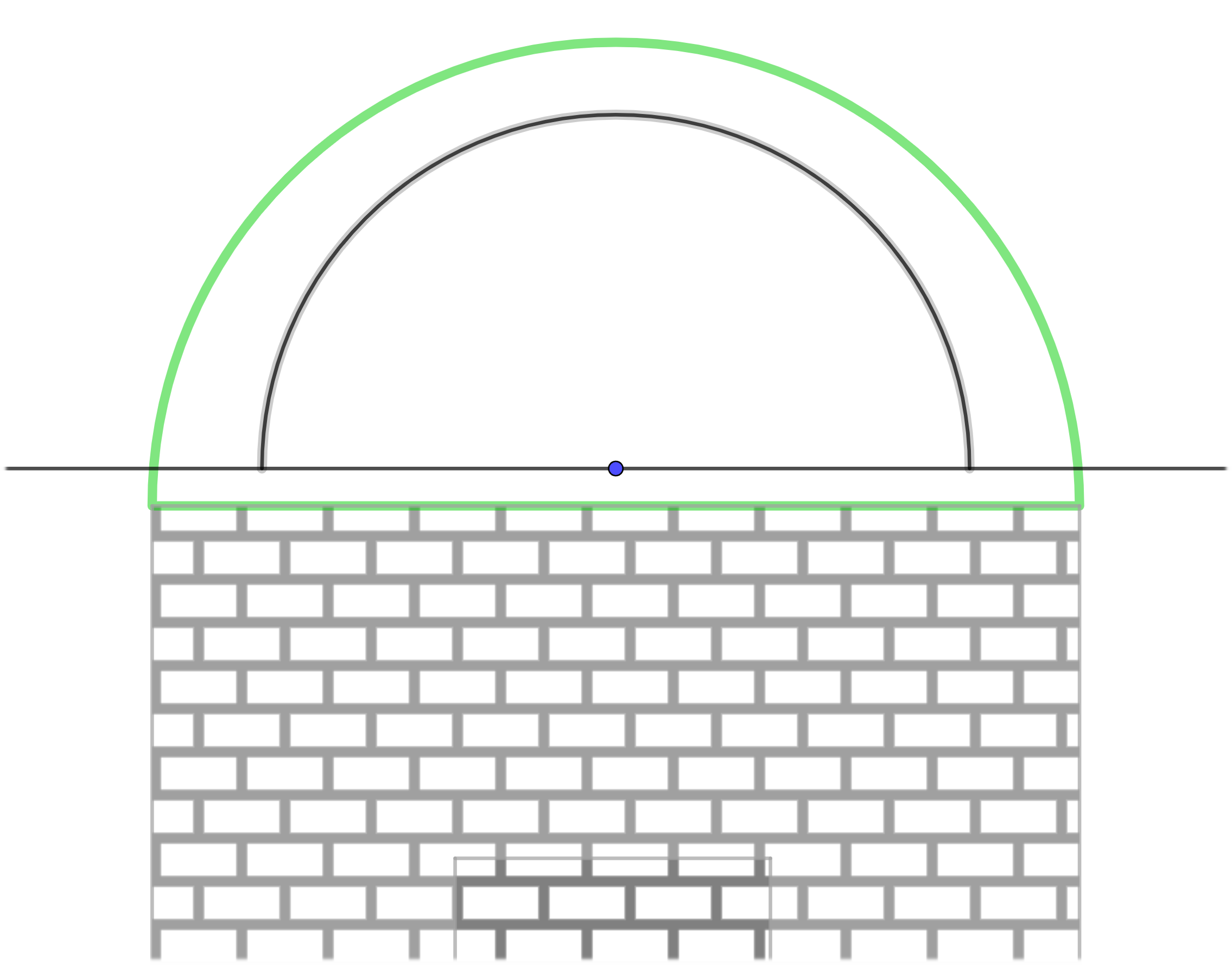
Si estamos trabajando con circunferencias, es porque la parte superior de nuestra caseta es un semicírculo.
Entonces, ¿cómo sería el plano de la maqueta de esta caseta?
Vamos a ver cómo sería una maqueta de cada una de las partes de nuestra caseta a escala 1:100. Es decir, un centímetro de la maqueta se corresponde con 100 cm de la longitud real, con un metro.
Una vista en 3D
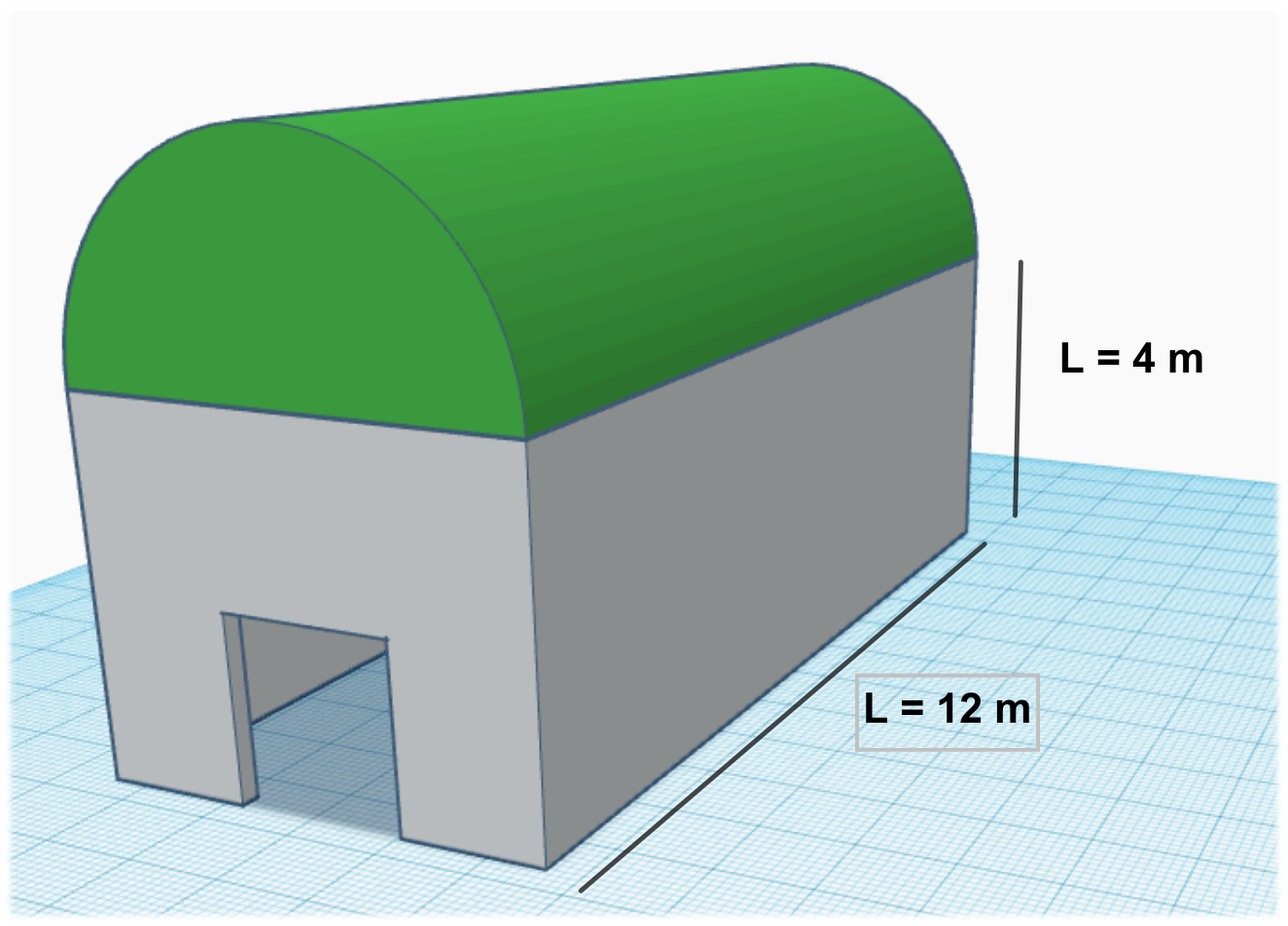
En la siguiente imagen se muestra cómo sería la maqueta de nuestra caseta que se caracteriza por tener el la parte superior del frontal con forma de semicircunferencia. Esto hace que el techo tenga forma cilíndrica, concretamente de medio cilindro.
Vamos a ver cómo quedaría cada una de las partes que formarían la maqueta de esta caseta.
El frontal lo conocemos
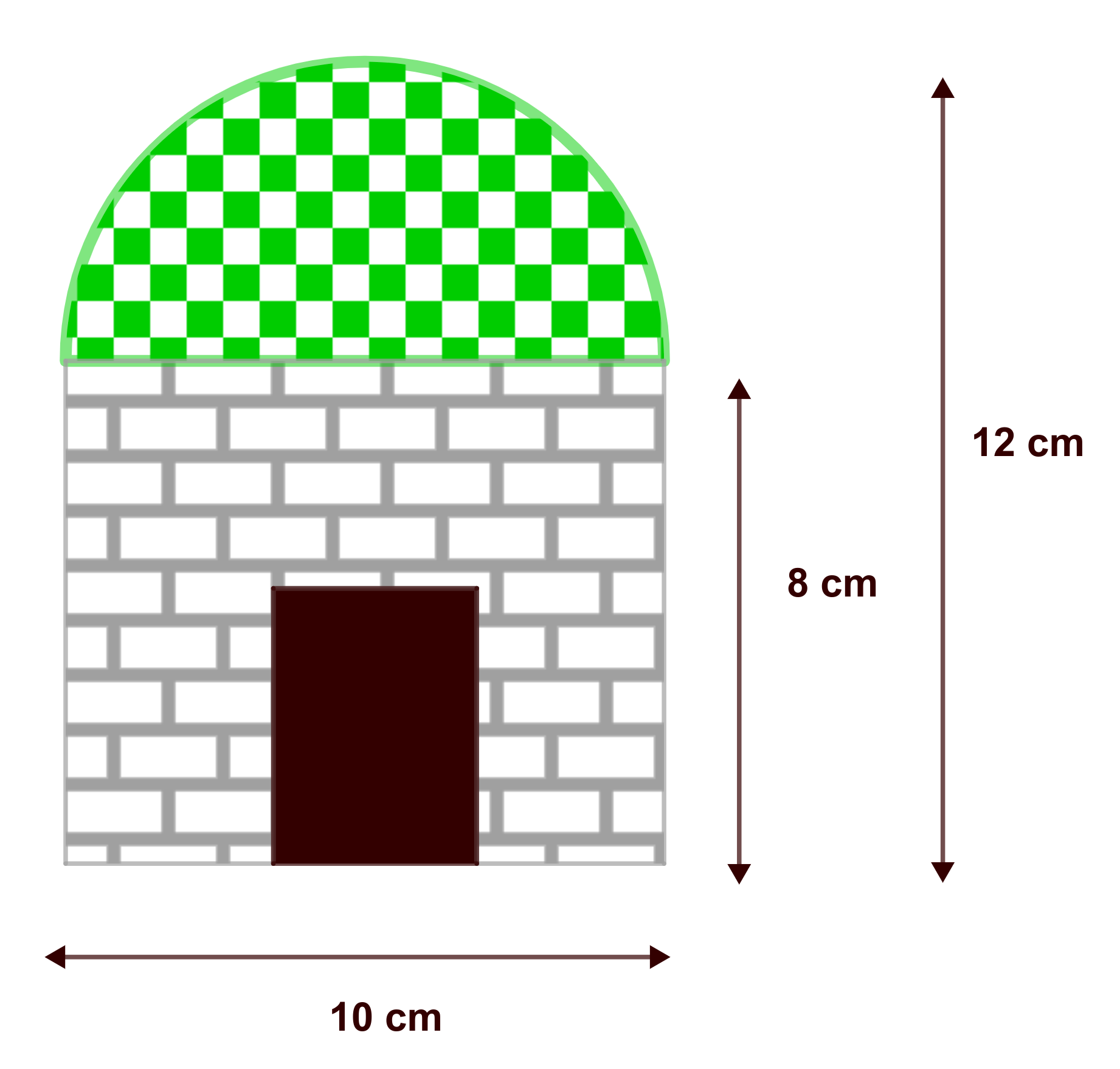
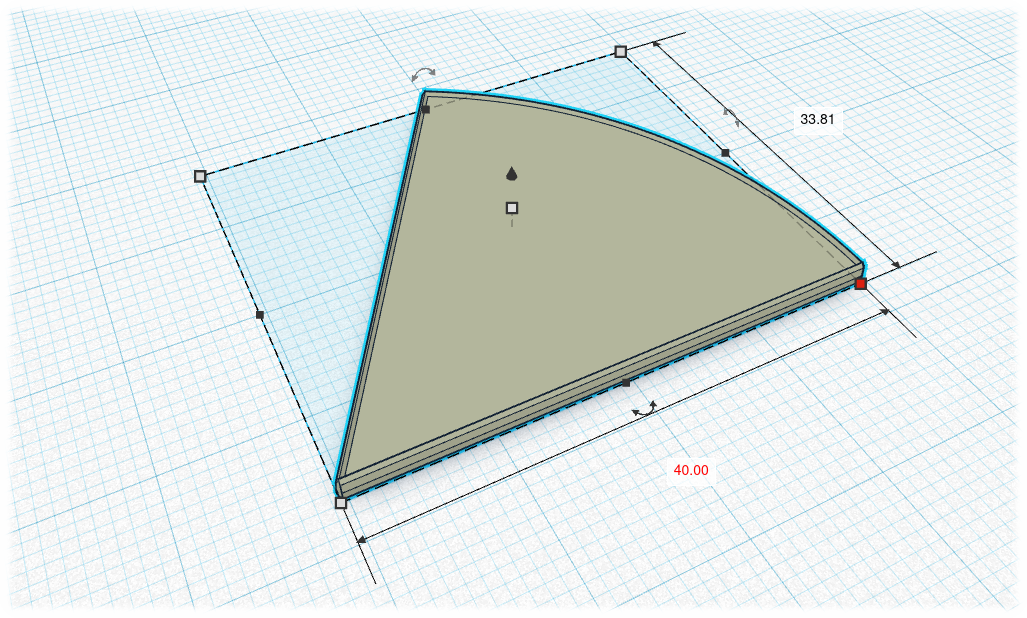
Imagina que tienes un frontal como el que aparece en la siguiente imagen, con estas dimensiones:
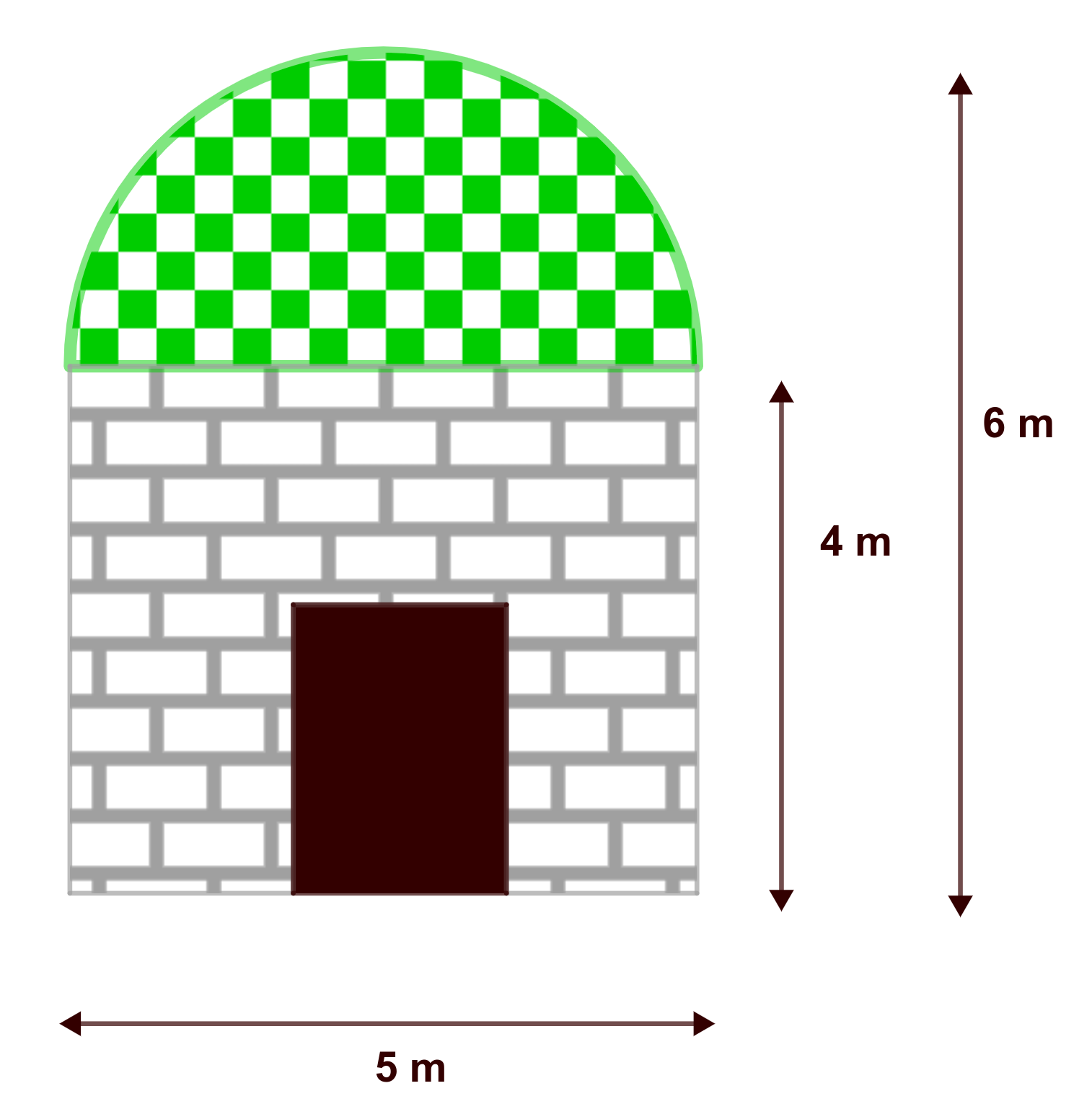¿Cuáles serían las longitudes de una maqueta a escala 1:100?
Anchura de la base → 5 metros = 500 cm, equivalen a 5 cm al dibujarlo en el papel.
Altura de la base rectangular → 4 metros equivalen a 4 centímetros
Altura total → 6 metros equivalen a 6 centímetros
Radio de la semicircunferencia → Esta medida es de 2 metros, equivalen a 2 centímetros.
La parte trasera de la caseta tendría la misma forma que el frontal.
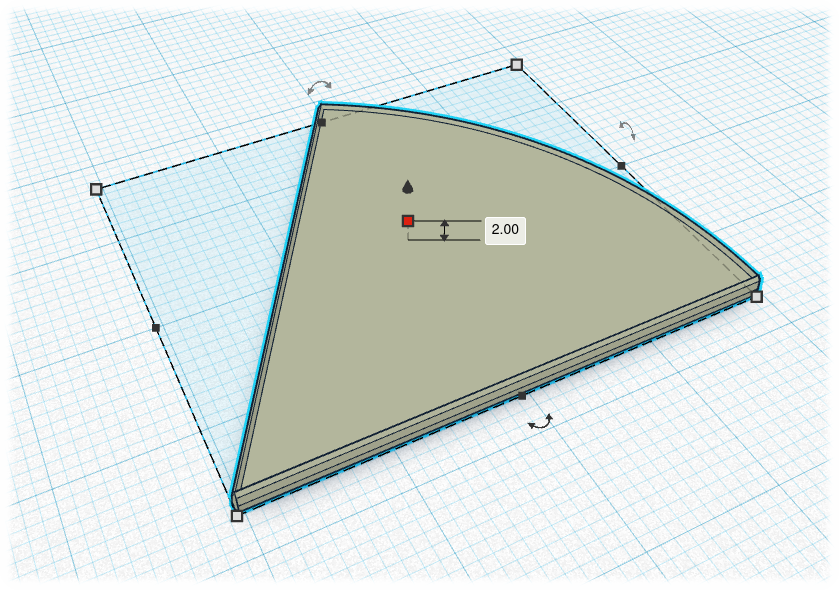
¿Cómo podrías dibujar la semicircunferencia? Marca el centro del lado superior del rectángulo y usa el compás para dibujar una semicircunferencia de radio igual a 2 cm.
¿Qué forma tiene el techo?
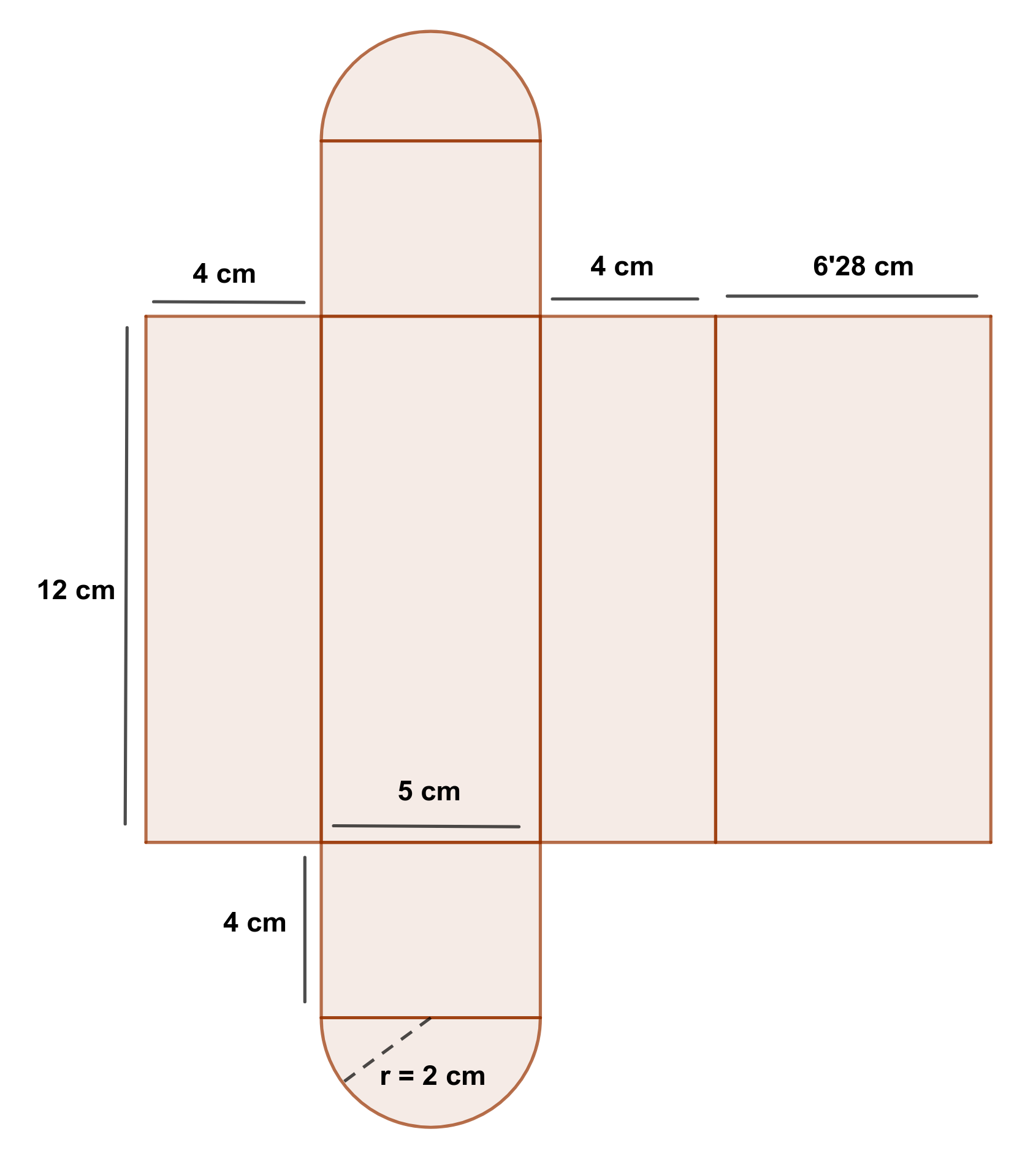
Como el frontal tiene forma de semicircunferencia, todo el techo será medio cilindro. Pero para hacer la maqueta, hay que tener en cuenta que el desarrollo de esta figura es de la siguiente manera:
Por lo tanto, como las partes semicirculares están incluidas en el frontal y en la pared trasera, solo habría que hacer el rectángulo que queda por encima. Pero, ¿qué dimensiones tiene ese rectángulo?
Está claro que el largo se corresponde con el largo de la caseta y que vendrá indicado en las dimensiones de la misma. Pero, ¿cuánto mide el ancho? E
sta parte se corresponde con el perímetro de la semicircunferencia sobre la que se apoya. Si en este caso el radio de la circunferencia es de 2 centímetros, el ancho del rectángulo será la mitad del perímetro de la circunferencia:
Como antes hemos visto que a escala 1:100 el radio es de 2 cm, la longitud sería la siguiente:
Ancho del techo → L = (2 · 3'14 · 2) : 2 = 6'28 cm
Largo del techo → Si en este caso se indica que la caseta tiene de largo 12 metros (como se ponía en un ejemplo de la página 3), equivalen a 12 centímetros.
¿Y los laterales?
Una vez hechas las partes frontal y trasera y el techo, las paredes laterales son muy fáciles de ver: se corresponde con dos rectángulos cuya altura es igual a la del rectángulo de frontal y cuya base se corresponde con el largo de la caseta. Si tenemos las siguientes dimensiones, vamos a ver la longitud de las partes de la maqueta:
Altura del lateral → 4 metros = 400 centímetros, equivalen a 4 centímetros.
Largo de la base → 12 metros equivalen a 12 centímetros.
¿Cómo quedaría la maqueta en papel?
Una vez tomadas todas las medidas de la maqueta, el modelo que hay que dibujar en papel para recortarlo y montarlo quedaría de la siguiente manera:
3. ¿Te atreves con el diseño?
Todo lo anterior es muy importante. Pero, ¿Cómo lo puedo utilizar para hacer que mi caseta de feria sea la más bonita de todas, la que tiene una portada más llamativa?
Una parte muy importante para hacer nuestra caseta es el diseño del frontal y de cualquier otra parte exterior que quieras. ¿Te atreves a hacer un diseño que atraiga al público utilizando algunos de los elementos matemáticos que se han visto anteriormente?
Opción A. Lo pasamos a un diseño
Antes de nada, prepara un modelo a escala 1:50 del frontal que ves en la siguiente imagen para hacer los diseños que se piden en las siguientes actividades.
¿Cómo podrías utilizar los sectores circulares para el diseño de tu caseta?
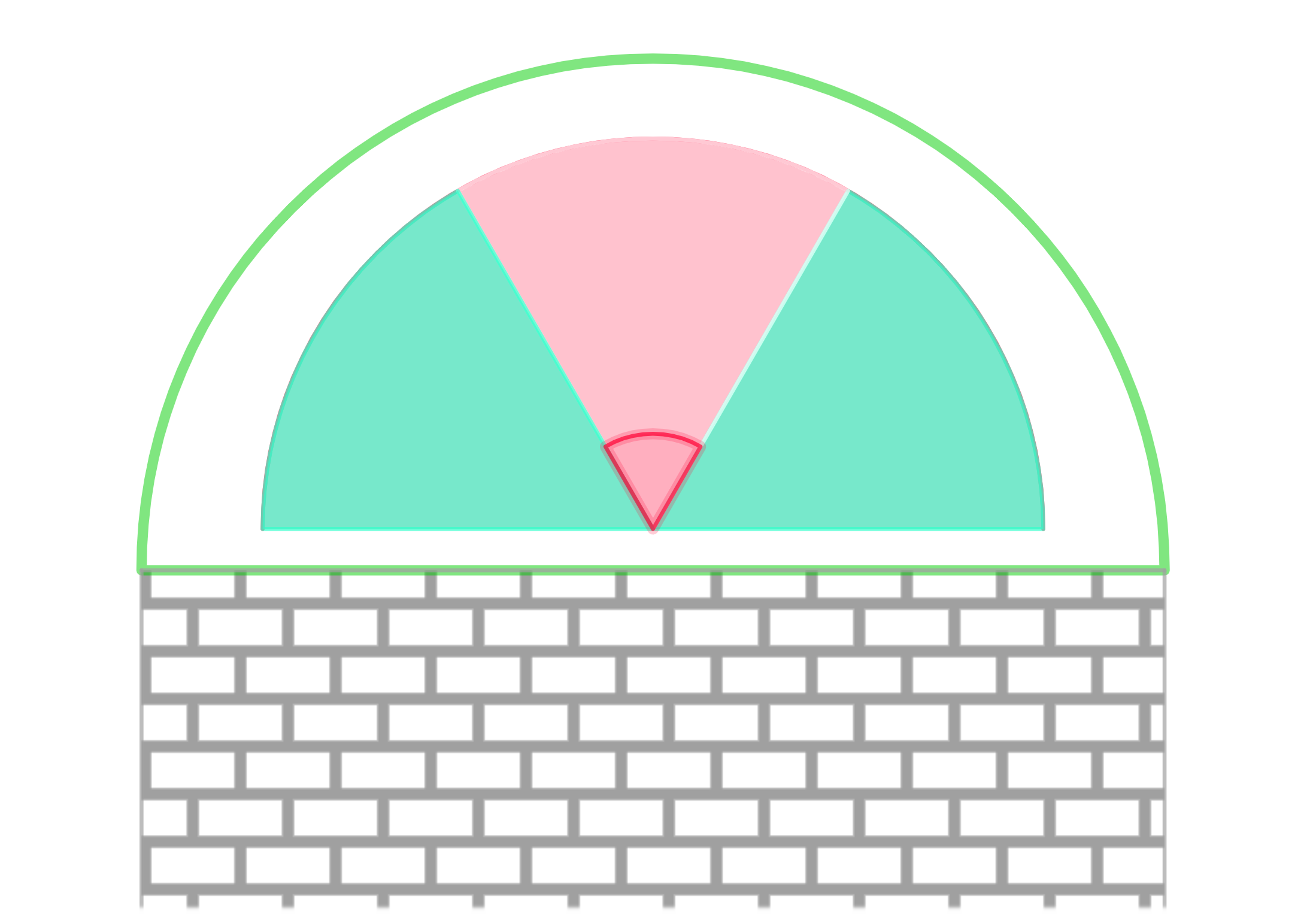
Muy fácil, sigue los siguientes pasos para decorar el frontal de tu caseta con sectores circulares que podrás poner de diferentes colores o con diferentes adornos.
La portada
Partiendo de la portada de tu caseta con forma semicircular, traza una línea por encima de la parte superior y busca su centro. Puedes hacerlo midiendo o con un compás.
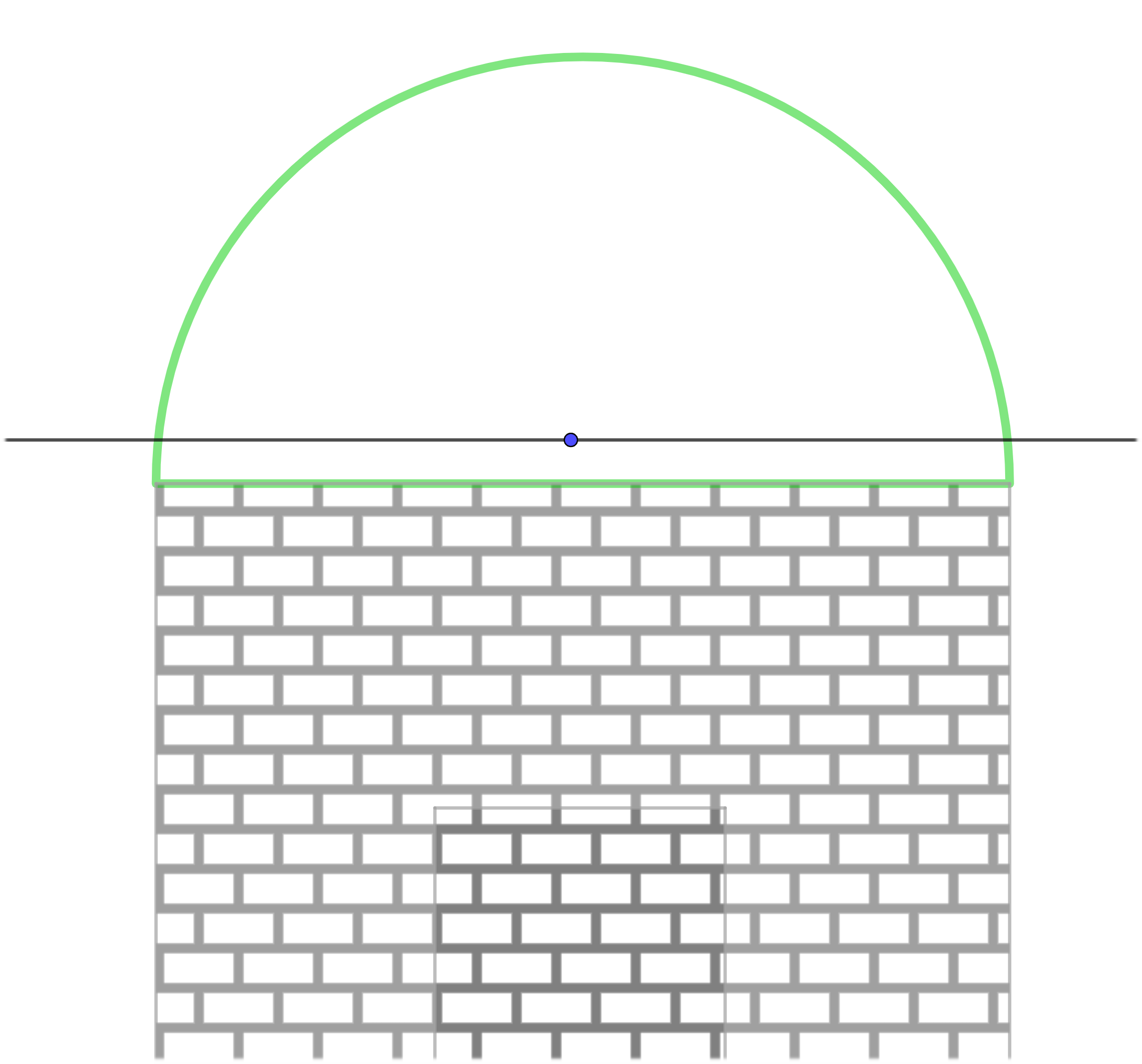
Para hacerlo con regla y compás, sitúa el compás en cada punto de corte de la recta con la caseta, abre un poco más de lo que mide el centro y traza dos circunferencias. Une la intersección superior e inferior y el punto donde corta con la primera recta es el centro.
Traza la semicircunferencia
Con el compás en el centro marcado, abre un poco menos de lo que mide el sector circular y traza una semicircunferencia:
- ¿En cuántas partes quieres dividir la semicircunferencia?
- ¿Qué ángulo tendrá cada sector circular?
- Calcula el área que tendrá cada sector.
Dibuja los sectores
Ahora solo queda trazar los sectores circulares que quieras y decorarlo.
Por ejemplo, si has decidido dibujar tres sectores, solo tendrás que marcar el ángulo calculado y dividir la semicircunferencia en tres partes iguales. Para ello necesitarás un transportador de ángulos.
Opción B. ¿Con cuántas partes trabajamos?
Solución
Solución
Solución
Solución
Opción C. No olvides el nombre
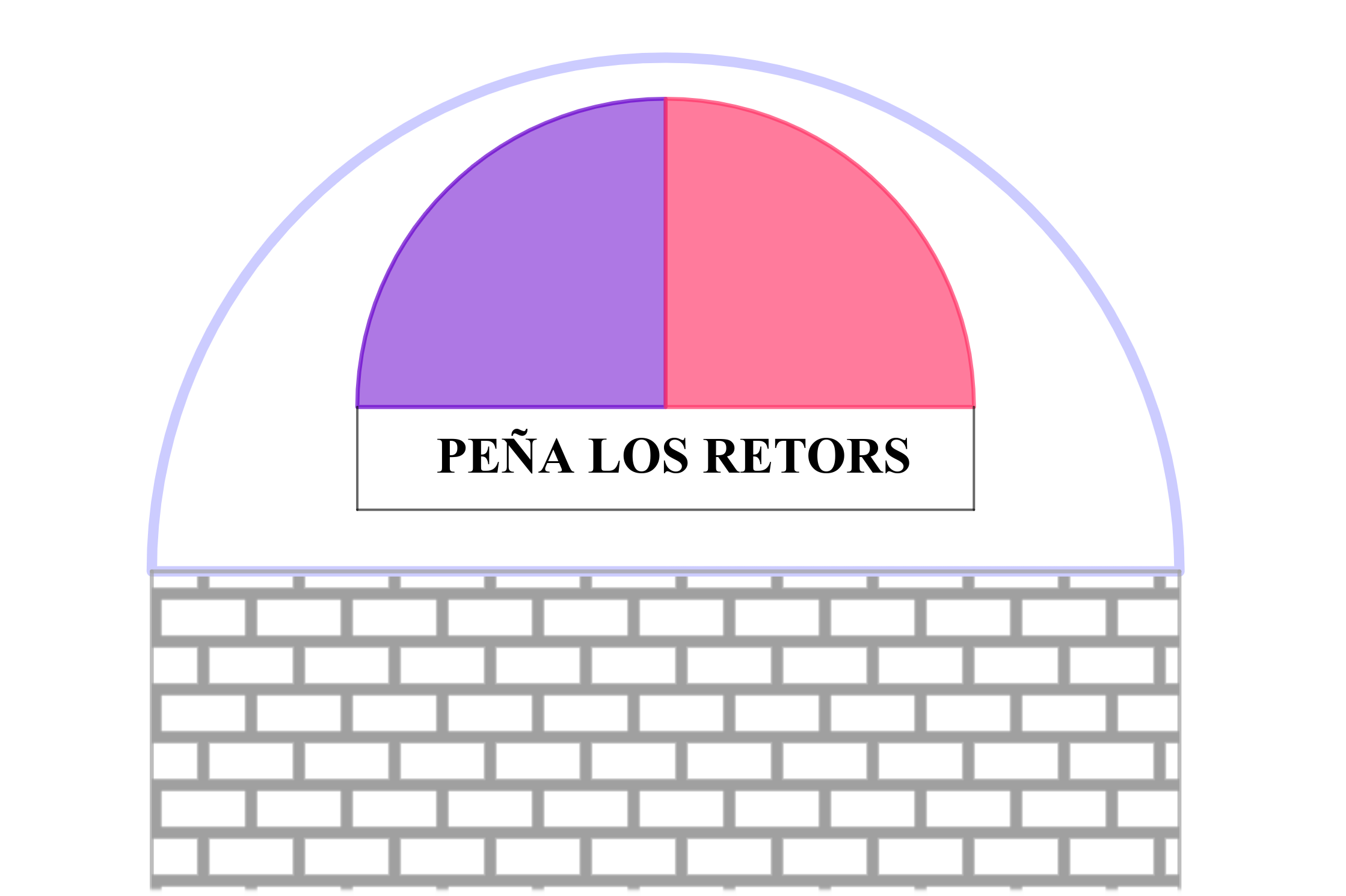
A la hora de diseñar la portada de nuestra caseta, también podemos poner el nombre visible en la parte superior con un cartel. De esta forma, no todo el espacio de la semicircunferencia superior será utilizado en decorar con sectores circulares.
Fíjate en la imagen y haz un diseño similar para tu caseta.
¿Ayuda con las medidas?
Si has tenido algún problema al calcular las medidas que debe tener el frontal de la caseta, puedes tomar el siguiente esquema del frontal de la caseta a escala 1:50 y completar la decoración con sectores circulares:
Para completar el diseño con los sectores circulares, puedes guiarte de los siguientes pasos para completar tu diseño:
- Dibuja un rectángulo centrado en la semicircunferencia del frontal de la caseta.
- Por encima de este rectángulo y con radio igual a la mitad de su longitud, dibuja dos, tres o cuatro sectores circulares diferentes.
- Escribe un nombre para tu caseta dentro del rectángulo. ¿Qué superficie ocupa el nombre de la caseta?
- Colorea cada uno de los sectores circulares. ¿Qué ángulo tiene cada uno de los sectores circulares que has dibujado y qué superficie ocupan?
Opción D. Pasamos al diseño en 3D
Decora el frontal de tu caseta con sectores circulares que podrás poner de diferentes colores o con diferentes adornos, y utiliza para ello cualquier programa de diseño.
Puedes usar geogebra
¿Te atreves a diseñar tus propios sectores circulares para la portada de tu caseta e imprimirlos en 3D?
Abre el programa Geogebra en tu ordenador o en tu dispositivo móvil y completa los siguientes pasos.
Dos puntos en el plano
Representa dos puntos en el plano de la pantalla de Geogebra.
Para facilitar la representación, es conveniente que tengan la misma coordenada Y.
Una rotación
Para formar adecuadamente el sector circular, hay que rotar el punto A respecto a B el ángulo que quieras que tenga tu sector.
Esto depende del número de partes en las que quieres dividir la semicircunferencia, como se ha visto anteriormente.
Recuerda que si n es el número de sectores que quieres, el ángulo de cada uno es 180 : n.
Así, por ejemplo, si quiero 3 sectores, cada un tendrá un ángulo de 60º.
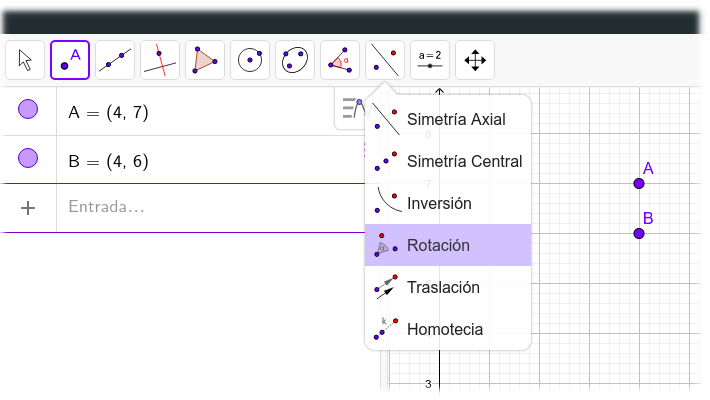
Por lo tanto, hay que hacer una rotación de 60º pulsando el botón que aparece en la imagen y seleccionando A y luego B.
Al hacerlo aparecerá una ventana para indicar el ángulo de rotación, el que tendrá el sector circular.
Al presionar OK aparecerá un nuevo punto en la pantalla.
Dibujar el sector
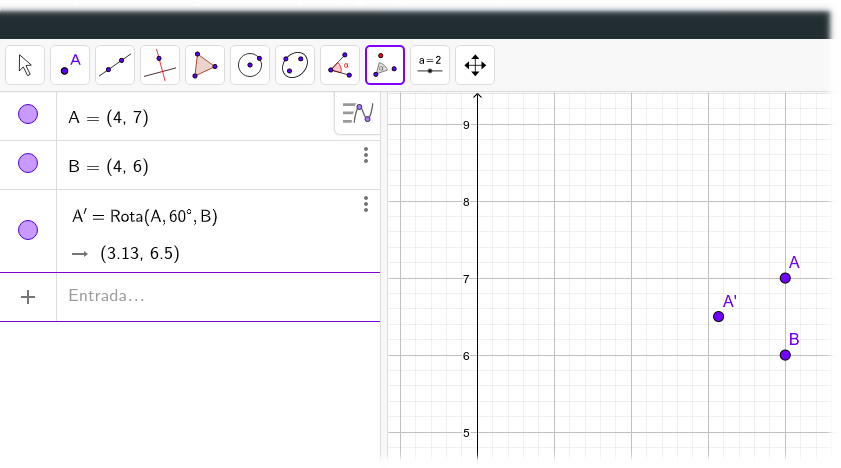
Selecciona la herramienta para dibujar un sector circular seleccionando primero el centro B y a continuación los pintos A y A'.
Al hacerlo aparecerá el sector circular comprendido en esos tres puntos y cuyo ángulo se corresponde con la rotación indicada anteriormente.
Ocultar lo que no sirve
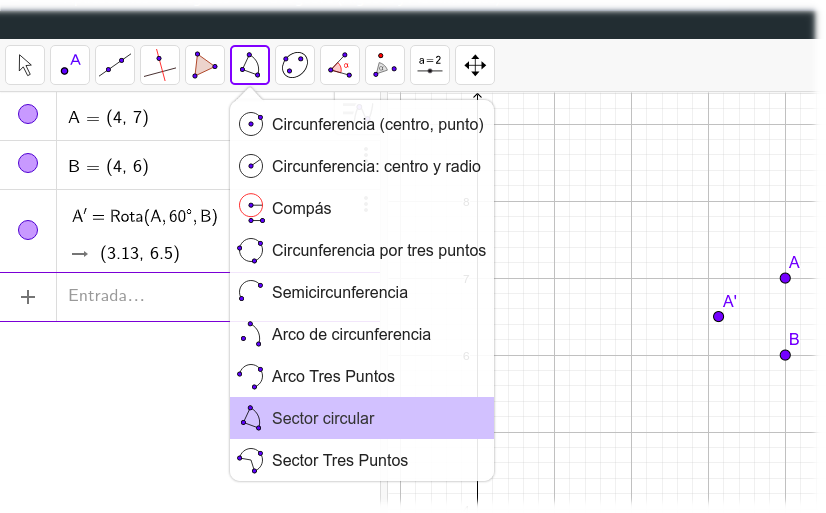
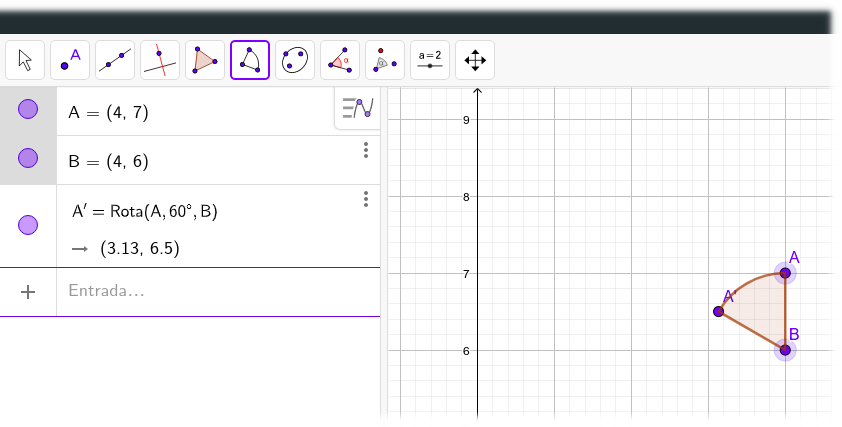
Para poder imprimir bien el sector circular, es necesario ocular varios objetos.
En primer lugar, pulsando sobre el plano de trabajo con el botón derecho del ratón, hay que ocultar los ejes y la cuadrícula.
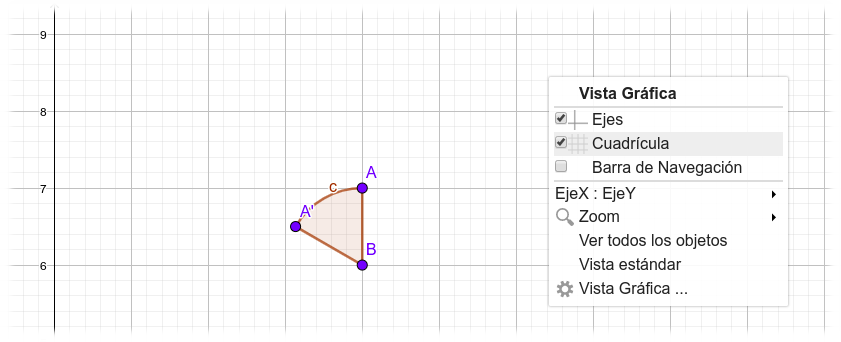
Al hacerlo el espacio de trabajo quedará en blanco, solo con el sector circular.
Para ocultar los puntos, basta con pulsar sobre cada círculo azul que hay en la parte izquierda de la pantalla y que representa a cada uno de los tres puntos.
Al hacerlo se pondrá blanco y no se verá el punto.
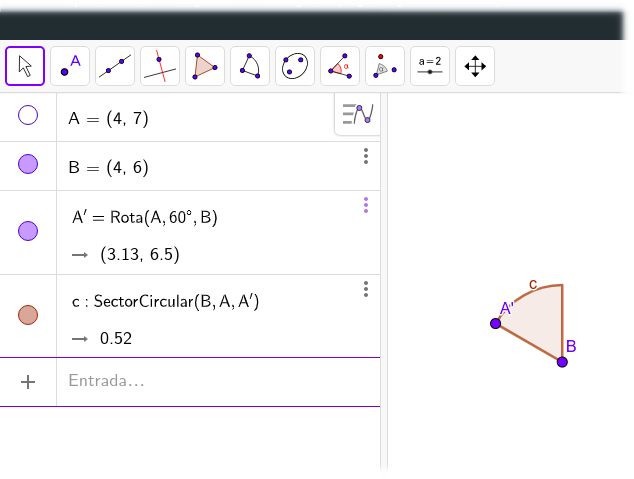Por último, hay que quitar el nombre del sector circular.
Basta con pulsar con el botón derecho sobre el sector y seleccionar la opción "etiqueta visible".
Preparar para la descarga
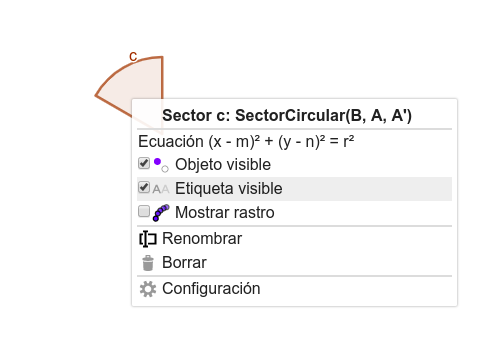
Para que el objeto se descargue correctamente, hay que modificar el grosor del trazo.
Pulsa con el botón derecho sobre el sector circular, selecciona configuración y dentro de la pestaña estilo modifica el valor grosor de trazo para dejarlo igual a 1.
Descargar archivo STL
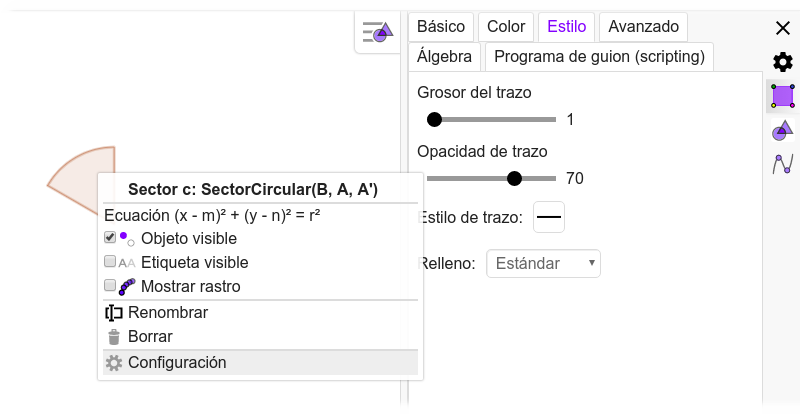
Accede al menú del archivo que hay en la parte superior derecha de la pantalla y selecciona archivo, descargar como y STL:
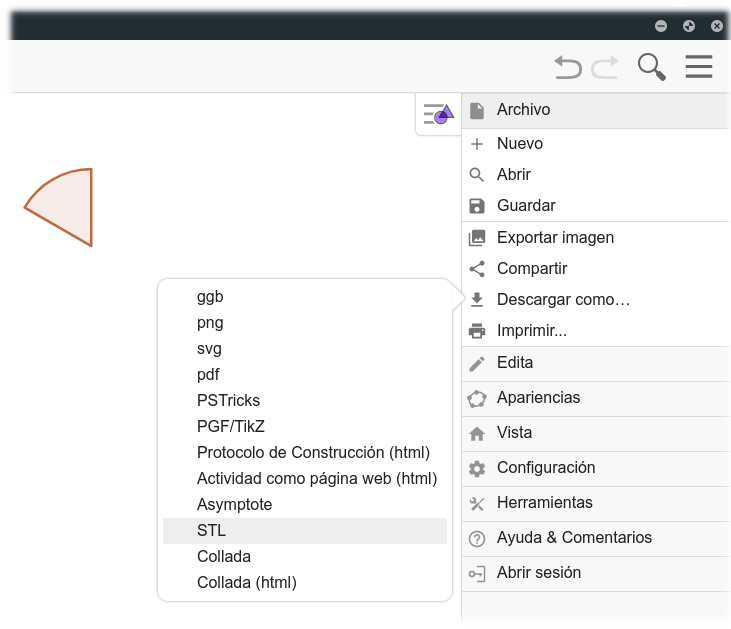
Al hacerlo aparecerá un cuadro con distintos valores para modificar.
Es importante poner la altura a 0.1 cm y el grosor a 1 mm. Luego pulsa descargar y guarda el archivo en tu dispositivo.
Vemos el diseño en 3D
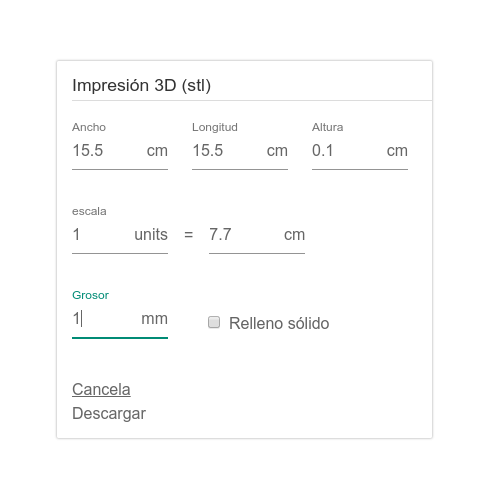
Para abrir el modelo 3D, puedes utilizar cualquier programa de diseño 3D.
Si lo haces desde este programa, accede a un nuevo diseño y selecciona la opción Importar que aparece en la parte superior derecha de la pantalla.
Busca el archivo en tu dispositivo.
Al seleccionar el archivo aparece una ventana para modificar el tamaño del diseño.
Para que no aparezca muy grande, puedes poner la escala al 50%.
Modifica el tamaño antes de imprimir
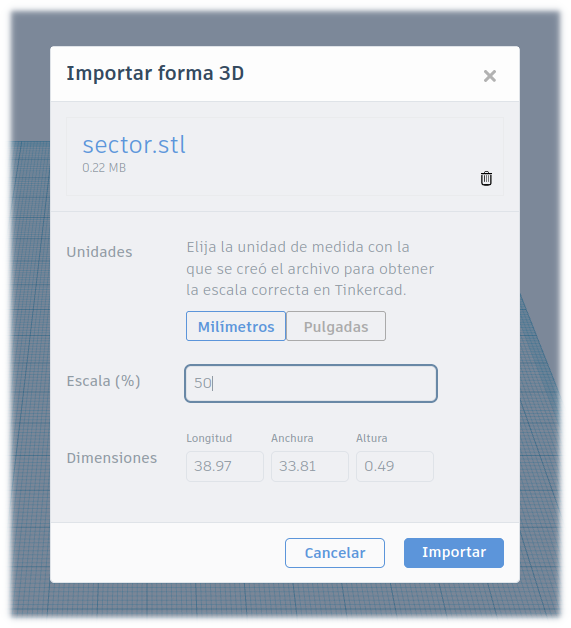
Antes de imprimir el archivo, puedes modificar las dimensiones ajustando al tamaño que quieres para tu caseta.
Si pulsas sobre el modelo y pinchas en una de las esquinas, aparece el valor de la longitud en milímetros.
Pulsa sobre el recuadro y escribe el valor en milímetros que quieres que tenga el lado del sector circular.
También es conveniente que ajustes la altura de la pieza y la dejes al menos a 2 milímetros pulsando en el recuadro blanco que queda sobre el sector circular.
Una vez ajustados estos valores a tu diseño, selecciona exportar y vuelve a guardar el archivo STL en tu dispositivo.
Listo para imprimir
Para imprimir el modelo, hay que generar el archivo gcode con cualquier programa de impresión 3D.
Abre el programa, selecciona tu archivo STL y ajusta los parámetros de impresión:
- Tipo de filamento: PLA
- Temperatura de extrusión: 200º
- Temperatura de la cama: 50º
- Relleno: 20%
- Color, el que más te guste para tu diseño
4. ¿Sabías que...?
El círculo es la figura geométrica más usada y necesaria en la vida cotidiana.
Es una curva cerrada y podemos observar su forma en la ruedas de los coches, en el fondo de los vasos y de las latas de conservas o refrescos, en la forma de la pizzas, en los relojes, en los anillos, en las señales de tráfico, en una noria, en las rotondas, en las sartenes, en las monedas...
¿Te atreves a encontrar más círculos a tu alrededor?
Una de las construcciones mas curiosas que existen es el puente de Rakotzbrücke o puente del diablo. Fue construido para unir las dos orillas de un lago en el parque Kromlauer en Alemania, aunque su construcción fue solo estética ya que el propio puente junto con su reflejo en el agua crea un círculo perfecto.
Definición:
Alimentos envasados herméticamente para ser conservados durante mucho tiempo.
Ejemplo:
Mario tiene en su restaurante diferentes conservas.
5. Reviso lo que aprendo
Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido)
Recuerda:
- Pregunta a tu profesor o profesora si la rellenarás en papel o en el ordenador.
- Si la rellenas en el ordenador, ¡no te olvides de guardarla en tu ordenador cuando la termines!
¡Ánimo, que lo harás genial!
Motus dice: ¿Qué tal va todo?
Parecía que no, pero la geometría se esconde detrás de la decoración de muchas de las cosas que conocemos.
Seguro que con lo que has visto y aprendido de circunferencias y sectores circulares puedes hacer diseños fantásticos para una caseta de feria.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0