Triángulos
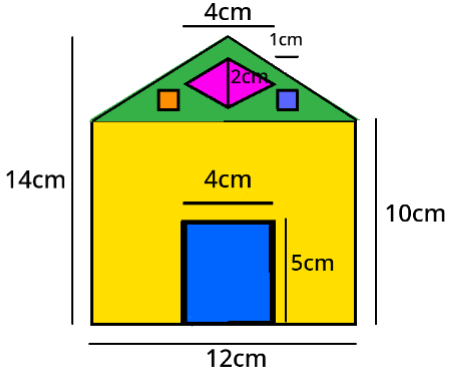
Ya has visto cómo los triángulos aparecen con frecuencia en las portadas de las casetas.
Si necesitamos saber la superficie que ocupan, necesitaremos conocer su área.
El área de un triángulo es el producto de su base por su altura dividido entre dos.
El borde de ese triángulo, su perímetro, se calcula como la suma de sus tres lados.
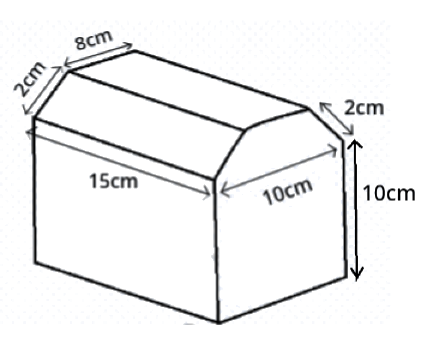
¿Cómo calcularías la superficie del friso del frontal de la caseta siguiente con forma de triángulo?


Conocemos su base que mide 12 cm, y su altura la podemos calcular restando 15-10=5cm.
Luego el área pedida es A=(12x5)/2=30cm2
Polígono regular
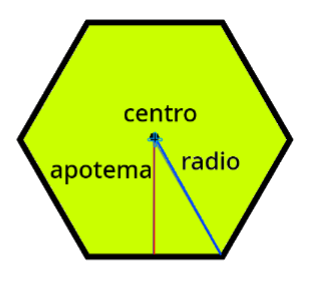
El área de un polígono regular es el producto de su perímetro por la apotema (que designamos por ap) dividido entre dos.
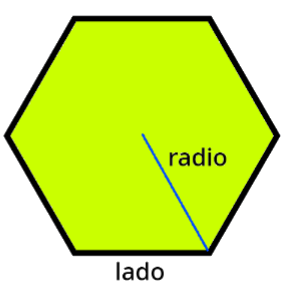
El perímetro se calcula sumando todos los lados o multiplicando la medida de un lado por el número de lados que tenga.
Vamos a intentar calcular el área del adorno con forma de pentágono regular que aparece en este frontal de caseta:

Los datos que nos aportan es que su radio mide 5 cm y que el lado mide 6 cm.
Para calcular el perímetro, basta hacer: Perímetro= 6+6+6+6+6= 6x5= 30cm
Para calcular su área, como sabemos que el área sigue la fórmula A=(P x ap)/2 debemos calcular anteriormente su apotema.

Estamos en la situación del Teorema de Pitágoras, teniendo como hipotenusa el radio del pentágono, y como catetos la apotema y la mitad del lado.
52=ap2+32 → 25=ap2+9 → ap2=16 → ap=4cm. Luego el área sería A=(30 x 4)/2=60cm2
Polígono no regular
En el caso de que tengamos un polígono no regular de más de 4 lados, para hallar su área tendríamos que descomponer en figuras más sencillas (triángulos o cuadriláteros fundamentalmente), que sabemos calcular su área.
El perímetro se hallaría sumando todos los lados del polígono.
Por ejemplo, si quisiéramos hallar el área y el perímetro de la fachada de la caseta siguiente:
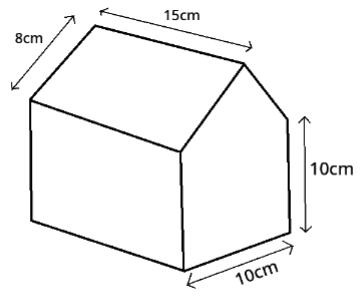

Tendríamos que descomponer en un triángulo por una parte y un cuadrado por otra parte y calcular sus áreas.
Área total= área del cuadrado + área del triángulo= (10 x 10) + (10 x altura del triángulo)/2

La altura del triángulo (h), la calculamos con el Teorema de Pitágoras, ya que es un cateto del triángulo rectángulo
82=h2+52 → 64=h2+25 → h2=64-25=39 → h= 6'24cm
Luego: Área total=(10 x 10) + (10 x altura del triángulo)/2=100+31'2= 131'2cm2
Por otro lado, y mucho más fácil y cómodo de calcular, el perímetro sería: P= 8+8+10+10+10= 46cm









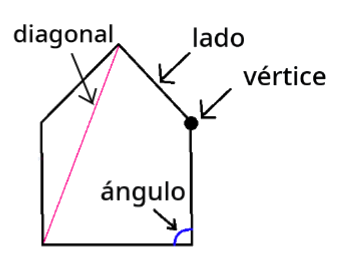









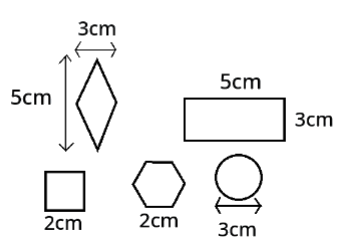
 Llega la hora de saber si eres capaz de calcular las áreas y perímetros de los polígonos que puedes utilizar para montar tu caseta.
Llega la hora de saber si eres capaz de calcular las áreas y perímetros de los polígonos que puedes utilizar para montar tu caseta.