Diccionario
Abstracto
Arista
El mundo en una caja
4.2. Volúmenes
Ya conocemos las figuras planas y cómo podemos calcular su área. Pero, ¡los objetos que queremos enviar no caben en ellas! Necesitamos objetos matemáticos para poder enviar aquello que deseemos.
¡Ven conmigo a pasear por la tercera dimensión!
1. Volumen y capacidad
Un cuerpo geométrico es una región cerrada del espacio.
Ya conoces muchos cuerpos geométricos:
Los cuerpos geométricos se clasifican en:
- Poliedros: si todas las superficies que lo delimitan son polígonos.
- Cuerpos redondos: si alguna de las superficies que lo delimitan son curvas.
El volumen de un cuerpo geométrico es la cantidad de espacio que ocupa. Se mide en unidades de volumen, que son las de longitud al cubo: $m^3$, $dm^3$, $cm^3$, ...
La capacidad de un cuerpo geométrico es la cantidad de espacio que hay dentro del cuerpo. Se mide en unidades de capacidad: litros, decilitros, centilitros, ...
Si pensamos en un cuerpo geométrico abstracto, por ejemplo un cilindro, el volumen y la capacidad coinciden puesto que está formada por superficies planas que no tienen volumen. Sin embargo, en la realidad, el volumen y la capacidad no coinciden nunca.
Piensa en un vaso con forma de cilindro. La capacidad del vaso es la cantidad de espacio que cabe dentro. Para calcularla podemos medir la cantidad de agua que puede contener. Sin embargo, el volumen del vaso es la cantidad de espacio que ocupa el vaso, que es mucho más pequeña. La puedes medir sumergiendo el vaso en un recipiente con agua y viendo cuánto aumenta el volumen del agua.
Otra forma de ver que capacidad y volumen no es lo mismo es la siguiente: piensa en un vaso de plástico y en otro de cristal que tengan la misma capacidad. El vaso de plástico es más fino. Por tanto, su volumen es menor.
Definición
Difícil de entender.
Lectura facilitada
Un cuerpo geométrico es
una región cerrada del espacio.
Ya conoces muchos cuerpos geométricos.
Los cuerpos geométricos se clasifican en:
- Poliedros: todas las superficies que lo delimitan
son polígonos.
- Cuerpos redondos: alguna de las superficies que lo delimitan
son curvas.
El volumen de un cuerpo geométrico
es la cantidad de espacio que ocupa.
Se mide en unidades de volumen
que son las de longitud al cubo:
som3, dm3, cm3, y otros.
La capacidad de un cuerpo geométrico
es la cantidad de espacio que hay dentro del cuerpo.
Se mide en unidades de capacidad:
l , dl, cl , y otros.
Piensa en un cuerpo geométrico abstracto,
por ejemplo un cilindro:
el volumen y la capacidad coinciden,
porque está formada por superficies planas
que no tienen volumen.
En la realidad,
el volumen y la capacidad no coinciden nunca.
Piensa en un vaso, tiene forma de cilindro.
Capacidad del vaso: cantidad de agua que cabe dentro.
Se calcula midiendo la cantidad de agua que cabe dentro.
Volumen del vaso: cantidad de espacio que ocupa el vaso.
Se puede medir sumergiendo el vaso en un recipiente con agua.
El volumen de aumenta, es la cantidad de espacio que ocupa el vaso.
Capacidad y volumen no es lo mismo.
Piensa en un vaso de plástico y otro de cristal
con la misma capacidad.
El vaso de plástico es más fino,
por tanto, su volumen es menos.
¿Quieres recordar las unidades de medida de volumen?
Las unidades de medidas de volumen
Son las medidas de longitud al cubo.
Un metro cúbico(m3) es el volumen
de un cubo de arista un metro.
Un decímetro cúbico (dm3) es el volumen
de un cubo de arista un centímetro.
Igual con las otras unidades.
1 decímetro = 10 centímetros.
1 decímetro cúbico = 10 X 10 X 10 = 1000 centímetros.
Para cambiar de unidad:
- Al pasar a una unidad inferior, multiplica x 1000.
- Al pasar a una unidad superior, divide entre 1000.
Ejemplos:
12 m3 = 12 x 1000 dm3 = 12.000 dm3.
12000 dm3 = 12000 x 1000 cm3 = 120.000 cm3
25m3 = 25: 1000 dam3 = 0´00025 hm3
0´025 dam3 = 0´025: 1000 hm3 = 0´000025 hm3
¿Quieres recordar las unidades de medida de volumen?
Las unidades de medida de volumen son las medidas de longitud al cubo.
Así, un metro cúbico ($m^3$) es el volumen de un cubo de arista un metro. Un decímetro cúbico ($dm^3$) es el volumen de un cubo de arista un centímetro, y lo mismo con las otras unidades.
De esta forma, como un decimetro son 10 centímetros, un decímetro cubico son $10\cdot 10 \cdot 10 =1000$ centímetros cubicos.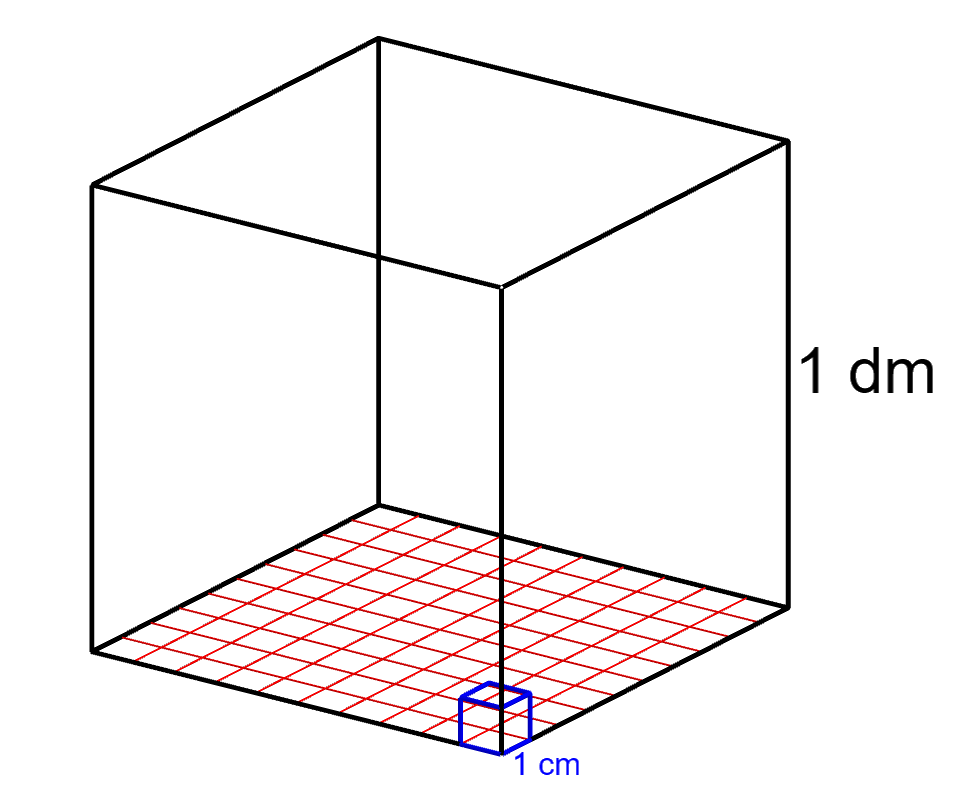 
Por tanto, para cambiar de unidad, al pasar a una unidad inferior hay que multiplicar por 1000 en vez de por 10 que se hace con las unidades de longitud. Y para cambiar a una unidad mayor hay que dividir por 1000, en vez de por 10 que se hace con las unidades de longitud.
Ejemplos:
$12 \ m^3=12 \cdot 1000\ dm^3 =12000\ dm^3 =12000\cdot 1000 \ cm^3 =12000000\ cm^3$
$25 \ m^3 =25 : 1000\ dam^3 =0.025 \ dam^3 = 0.025 : 1000 \ hm^3 =0.000025 \ hm^3$
2. Volumen y área de un cuerpo geométrico
El volumen de un cuerpo geométrico es la porción del espacio que ocupa.
El área de un cuerpo geométrico es la suma de las áreas de todas las superficies que lo forma.
Por ejemplo, con los paquetes de nuestra empresa de mensajería, el volumen de un paquete es espacio que ocupa, y el área del paquete es la suma de las áreas de las caras del paquete.
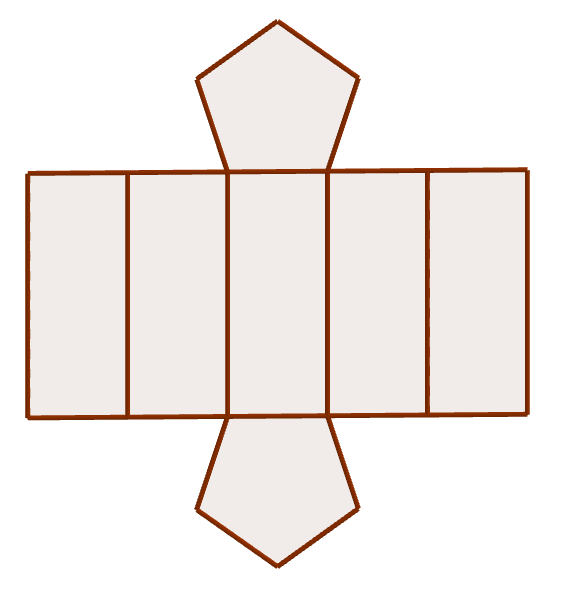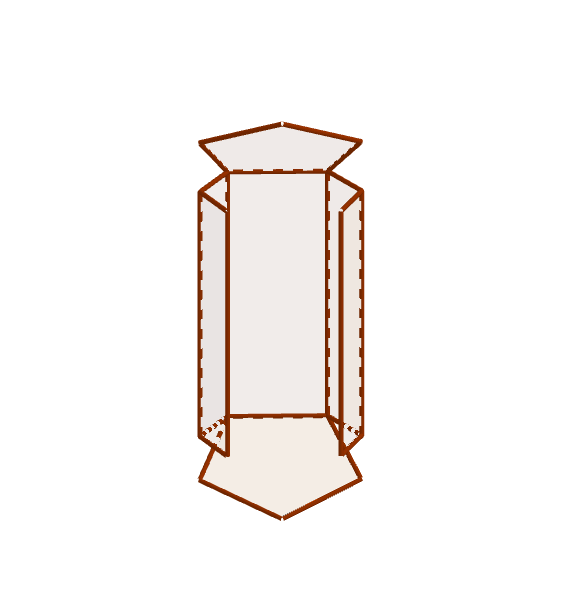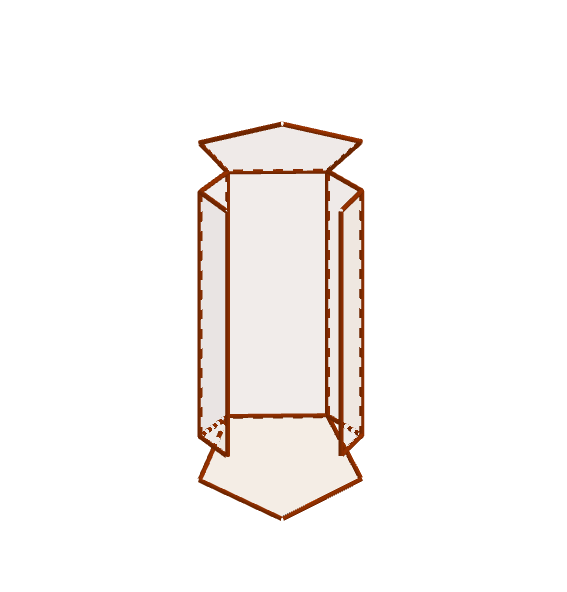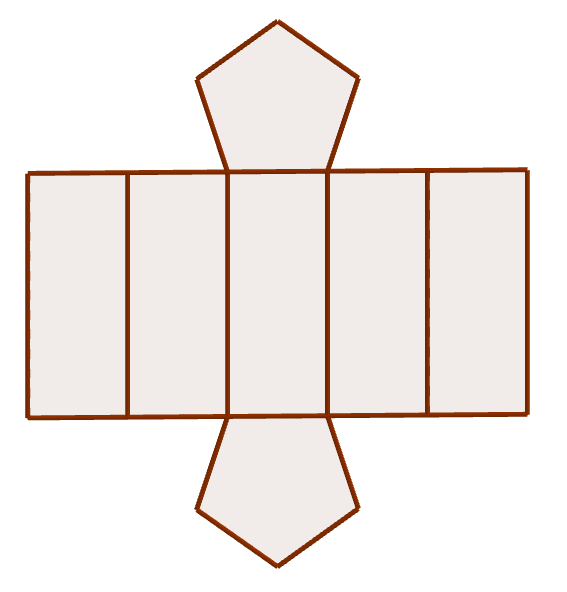
Desarrollo plano
Se llama desarrollo plano de un cuerpo geométrico a una figura plana tal que mediante dobleces sirve para construir el cuerpo geométrico.
Lectura facilitada
El volumen de un cuerpo geométrico es
la porción de espacio que ocupa.
El área de un cuerpo geométrico es
la suma de las áreas de todas las caras
que lo forma.
En nuestra empresa de mensajería
el volumen de un paquete es el espacio que ocupa
y el área del paquete es la suma de las áreas
de las caras del paquete.
Se llama Desarrollo Plano de un cuerpo geométrico
a una figura plana que mediante dobleces
sirve para construir el cuerpo geométrico.
3. Algunos cuerpos geométricos
Vamos a clasificar algunos de los cuerpos geométricos que más se utilizan, estudiando cómo se calcula su volumen y su área.
Algunos de estos cuerpos te van a ser muy útiles para diseñar los paquetes de la empresa de paquetería.
Prisma
Un prisma es un poliedro que tiene dos caras que son polígonos iguales y paralelos, que se llaman bases, y el resto son paralelogramos, y se llaman caras laterales.
Si las caras laterales son rectángulos se llama prisma recto y si las caras laterales no son rectángulos se llama prisma oblicuos.
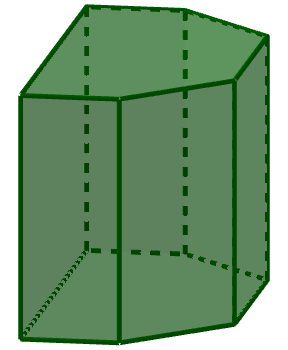
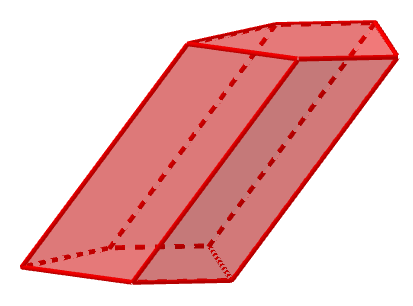
Se llaman prismas regulares a los prismas rectos cuyas bases son polígonos regulares.
El volumen de un prisma es igual al área de una base por su altura.
La altura de un prisma es la distancia entre las dos bases.
$V=A_b \cdot h$
Para calcular el área es fundamental conocer su desarrollo plano, que está compuesto por los dos polígonos de las bases y los paralelogramos de las caras laterales.
Ejemplo:
Calcula el volumen y el área del siguiente prisma triángular regular, en el que el lado de la base es 3 cm, la altura del triángulo de la base es 2.60 cm y la altura del prisma es 6 cm.
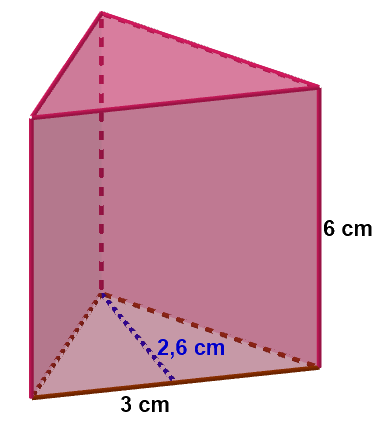
$\mbox{Área base}=\dfrac{\mbox{base}\cdot \mbox{altura}}{2}=\dfrac{3\cdot 2.6}{2}=\dfrac{7.8}{2}=3.9 cm^2$
$\mbox{Volumen}=\mbox{Área base}\cdot \mbox{altura}=3.9\cdot 6=23.4 cm^3$
El desarrollo plano de este prisma esta formado por los dos triángulos y los tres rectángulos de las caras laterales:
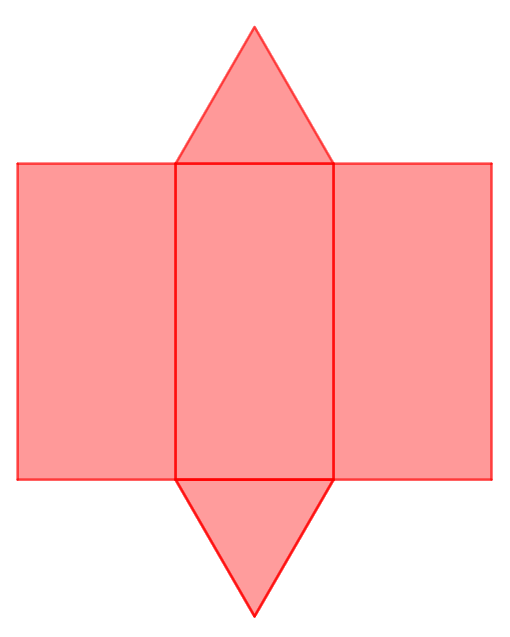
$\mbox{Área prisma}=2\cdot \mbox{área base}+3\cdot \mbox{área rectángulo}=2\cdot 3.9 +3\cdot 3\cdot 6=7.8+54=61.8 cm^2$
Cubo
Un cubo es poliedro que tiene seis caras que son cuadrados iguales.
Un cubo es un caso particular de prisma, en el que las bases son cuadrados y las caras laterales también.
Los dados con los que jugamos al parchís son cubos:
El volumen del cubo es igual al lado de un cuadrado elevado al cubo.
$V=l^3$
El área de un cubo es 6 por el área de un cuadrado, es decir, 6 por el lado al cuadrado.
$A=6l^2$
El desarrollo plano del cubo está formado por seis cuadrados.
Ejemplo:
Calcula el área y el volumen de este cubo de arista 5 dm.
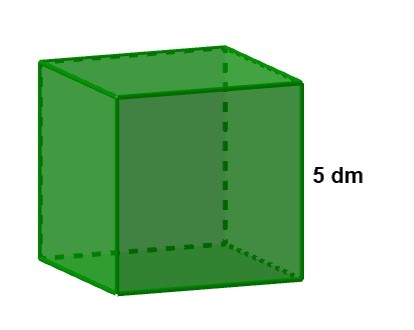
$\mbox{Área base}=\mbox{lado}^2=5^2=25 \ dm^2$
$\mbox{Volumen}=\mbox{lado}^3=5^3=125 \ dm^3$
El desarrollo plano está formado por seis cuadrados de lado 5 dm:
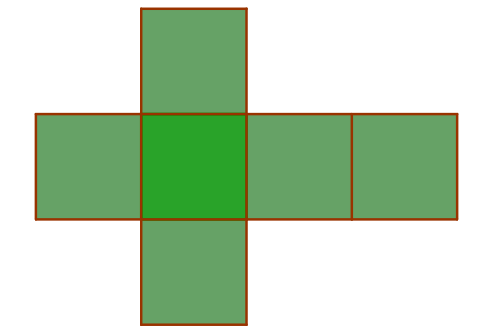
$\mbox{Área cubo}=6\cdot \mbox{lado}^2=6\cdot 5^2=6\cdot 25=150 \ dm^2$
Ortoedro
Un ortoedro es un poliedro formado por seis cara rectangulares paralelas dos a dos.
Es decir, un ortoedro es un prisma recto de bases rectangulares.
Este cuerpo geométrico es el que más vas a usar en este proyecto. Como has visto en actividades anteriores, y habrás podido comprobar por ti mismo, la gran mayoría de paquetes tienen forma de ortoedro.
Un ortoedro tiene tres aristas distintas, a la longitud de esas aristas se les llama ancho, largo y alto. El nombre que se le da a cada uno depende de cómo colocamos el ortoedro, pero para realizar los cálculos de su área y volumen da igual.
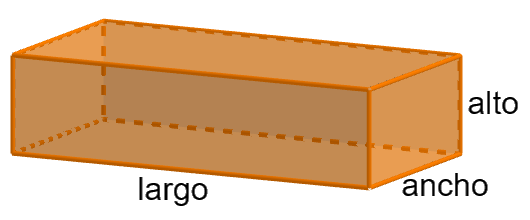
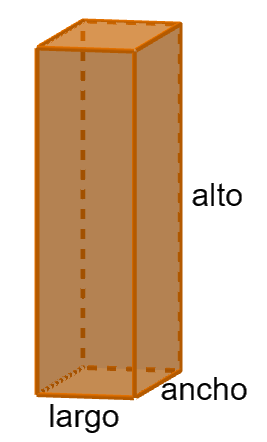
El volumen de un ortoedro, como es un prisma, se puede calcular multiplicando el área de la base por la altura.
Aunque lo que se suele usar es que el volumen de un ortoedro es igual al producto del largo por el ancho por el alto.
$\mbox{Volumen}=\mbox{largo}\cdot \mbox{ancho} \cdot \mbox{alto}$
El área del ortoedro es la suma de las áreas de los seis rectángulos que lo forman.
El desarrollo plano de un ortoedro está formado por seis rectángulos.
Ejemplo:
Calcula el área y el volumen de este cubo que mide 5 m de largo, 3 m de ancho y 9 m de alto.
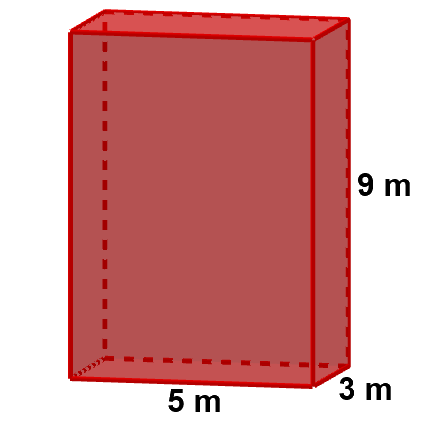
$\mbox{Volumen}=\mbox{largo}\cdot \mbox{ancho} \cdot \mbox{alto}=5\cdot 3 \cdot 9 =135 \ m^3$
El desarrollo plano es:
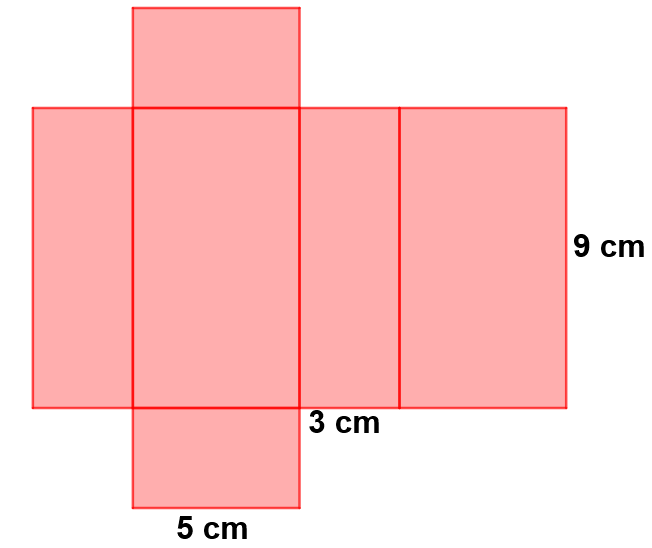
$\mbox{Área base}=5\cdot 3 =15 \ m^24$
$\mbox{Área cara frontal}= 5\cdot 9=45 \ m^2 $
$\mbox{Área cara lateral}=3\cdot 9 =27 \ m^2$
$\mbox{Área ortoedro}=2\cdot 24+2\cdot 45 +2\cdot 27 = 48+90+54=192 \ m^2$
Cilindro
Un cilindro es el cuerpo geométrico que se obtiene al girar un rectángulo sobre uno de sus lados.
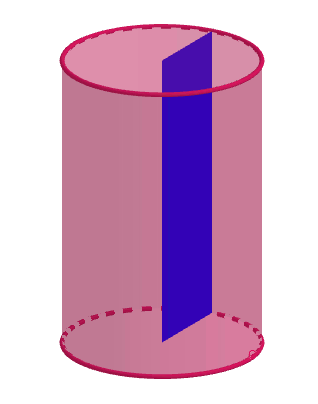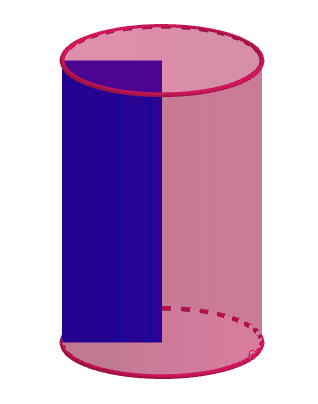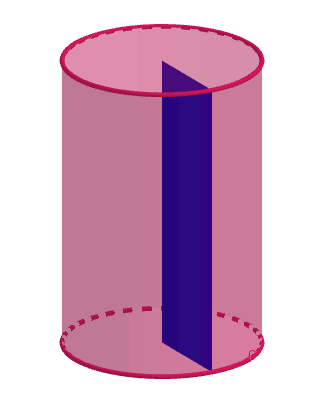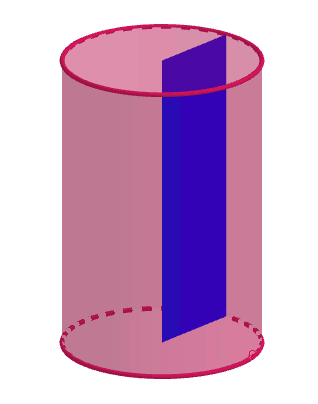
Un cilindro es como un prisma en el que las bases son círculos, pero no podemos decir que es un prisma porque los prismas son poliedros y están formados sólamente por polígonos.
El cilindro es uno de los cuerpos geométricos que más se utiliza, por ejemplo, la mayoría de latas de conservas, las latas de bebidas, las latas de pintura, ...
El volumen de un cilindro es el producto del área de la base por su altura.
Como la base del cilindro es un círculo, el área de la base es igual al producto de $\pi$ por el radio al cuadrado
$\mbox{Volumen}=\mbox{Área base}\cdot \mbox{altura} = \pi \cdot r^2 \cdot h$
El desarrollo plano de un cilindro está formado por los dos círculos de las bases y un rectángulo, que sale de despleglar la superficie lateral.
Por tanto, el área de un cilindro es dos veces el área del círculo más el área del rectángulo lateral que tiene como base la longitud de la circunferencia y como altura la altura del cilindro.
$\mbox{Área base}= 2 \cdot \pi \cdot r^2 +2 \cdot \pi \cdot r \cdot h = 2 \cdot \pi \cdot r \cdot (r+h)$
Ejemplo:
Calcula el área y el volumen de este cilindro que mide 6 dam de altura y su radio mide 4 dam.
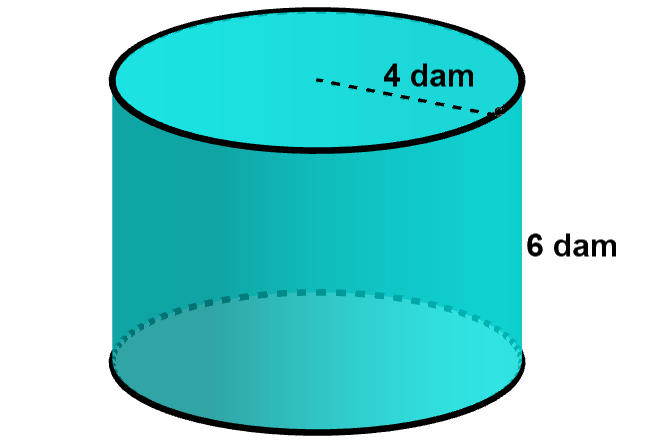
$\mbox{Volumen}=\pi r^2 h=\pi \cdot 4^2\cdot 6 =96 \pi \approx 301.59 \ dam^3$
$\mbox{Área}=2 \pi r^2 +2 \pi r h =2\pi \cdot 4^2 +2\pi \cdot 4 \cdot 6 =32 \pi +48 \pi = 80 \pi \approx 251.33 \ dam^2$
Pirámide
Una pirámide es un poliedro que está formado por un polígono, que llamamos base, y resto de caras son triángulos con vértice en común.
Los triángulos se llaman caras laterales, y el vértice en común se llama cúspide.
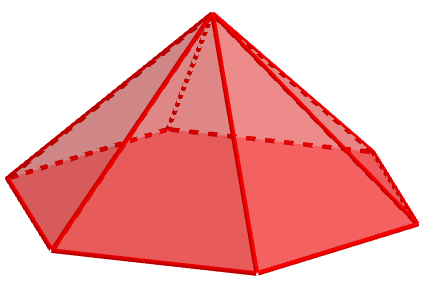
Las pirámides más famosas son las de Egipto.
El volumen de una pirámide es igual a un tercio del área de la base por su altura.
La altura de una pirámide es la distancia de la base a la cúspide.
$\mbox{Volumen}=\dfrac{1}{3}\mbox{área base}\cdot \mbox{altura}$
Para calcular el área es fundamental conocer su desarrollo plano, que está compuesto por el polígono de la base y los triángulos laterales..
¡Importante! no confundir la altura del triángulo, que es la distancia de la cúspide a la base, con la altura de las caras laterales, que es la distancia de la cúspide a la base del triángulo.
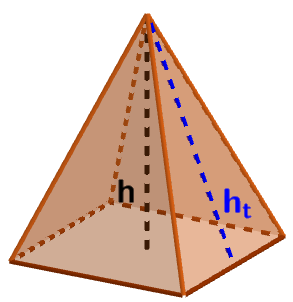
h es la altura de la pirámide
ht es la altura de la cara lateral
Ejemplo:
Calcula el volumen y el área de esta pirámide cuadrangular en la que la arista de la base mide 3 cm, la altura de la pirámide es 5 cm y la altura de la cara lateral es 5.22 cm.
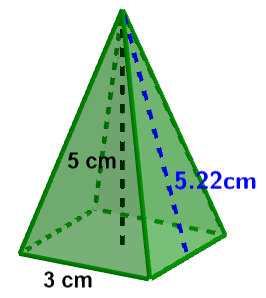
$\mbox{Volumen}=\dfrac{1}{3}\cdot \mbox{área base} \cdot \mbox{altura} =\dfrac{1}{3} \cdot 3^2 \cdot 5 = 15 \ cm^3$
Para calcular el área dibujamos el desarrollo plano:
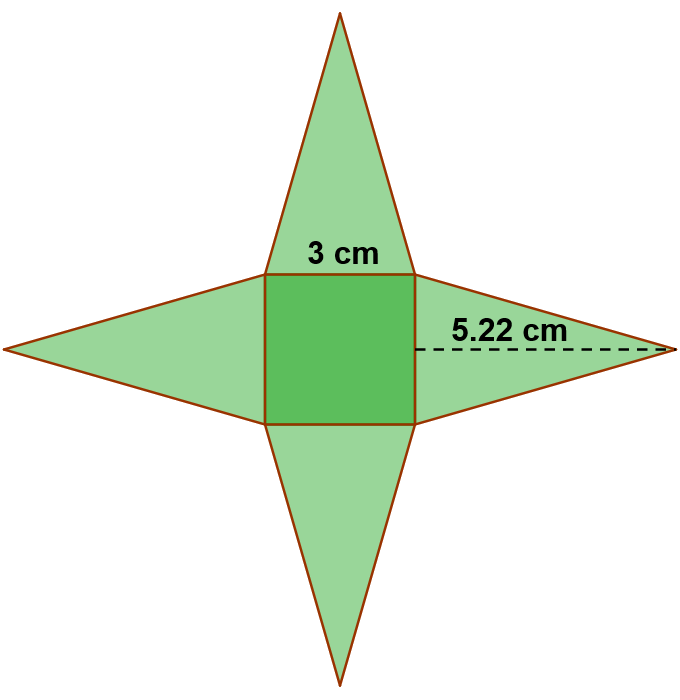
El área es igual al área del cuadrado de la base más el área de los cuatro triángulos laterales.
$\mbox{Área}=\mbox{área base} + 4\cdot \mbox{área triángulo} = 3^2 +4\cdot \dfrac{3\cdot 5.22}{2} = 9 + 7.83 = 16.83 \ cm^2$
Cono
Un cono es el cuerpo geométrico que se obtiene al girar un triángulo rectángulo sobre uno de sus catetos.
Un cono es como una pirámide en el que la base es un círculo, pero no podemos decir que es una pirámide porque las pirámides son poliedros y están formados solamente por polígonos.
La altura del cono es la distancia de la cúspide.
Se llama generatriz a cualquiera de los segmentos que une la cúspide con un punto de la circunferencia que genera la base. Es la hipotenusa del triángulo que genera el cono.
El cono es un cuerpo geométrico que se utiliza mucho:
El volumen de un cono es igual a un tercio del producto del área de su base por la altura del cono.
$\mbox{Volumen}=\dfrac{1}{3}\cdot \mbox{área base} \cdot \mbox{altura} =\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h$
El desarrollo plano de está formado por el círculo de la base y un sector circular que resulta al desplegar el lateral.
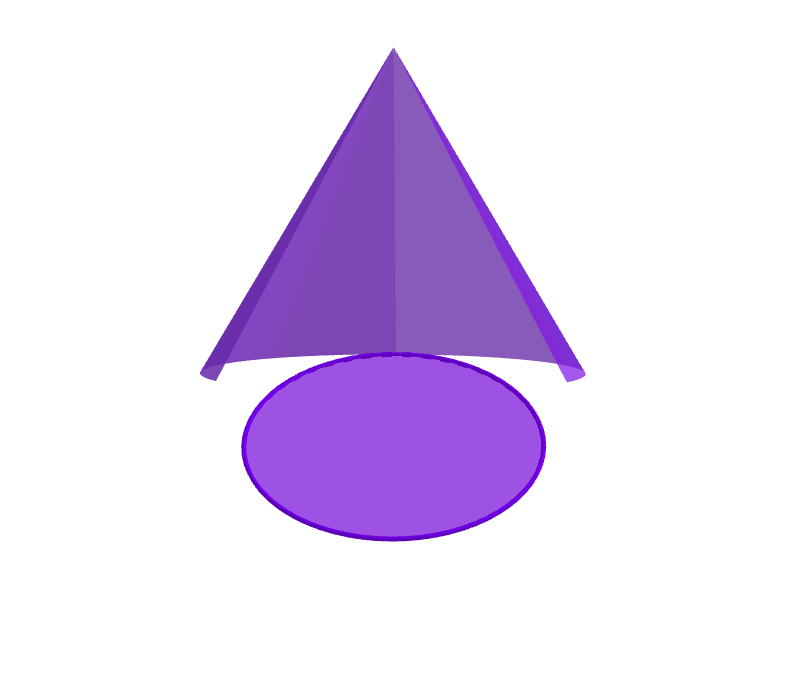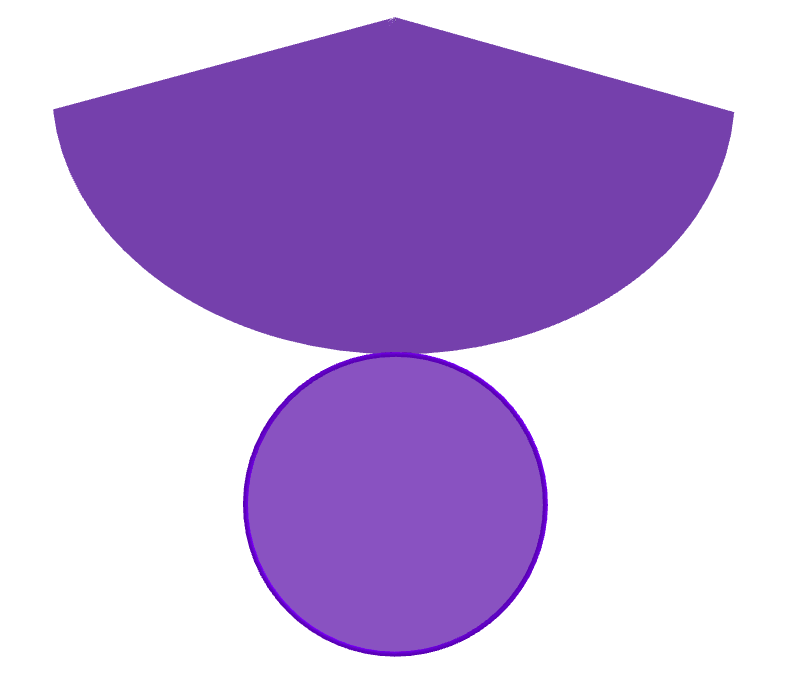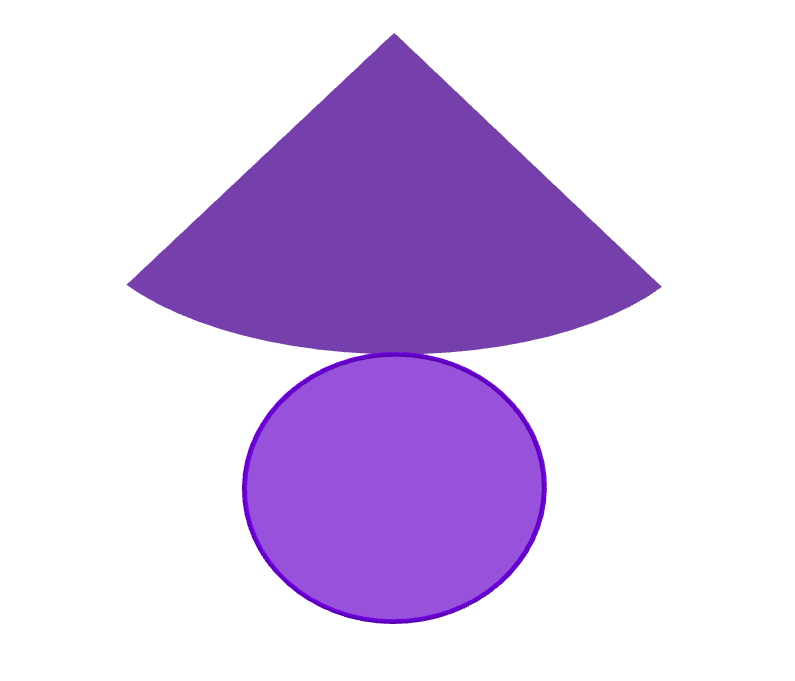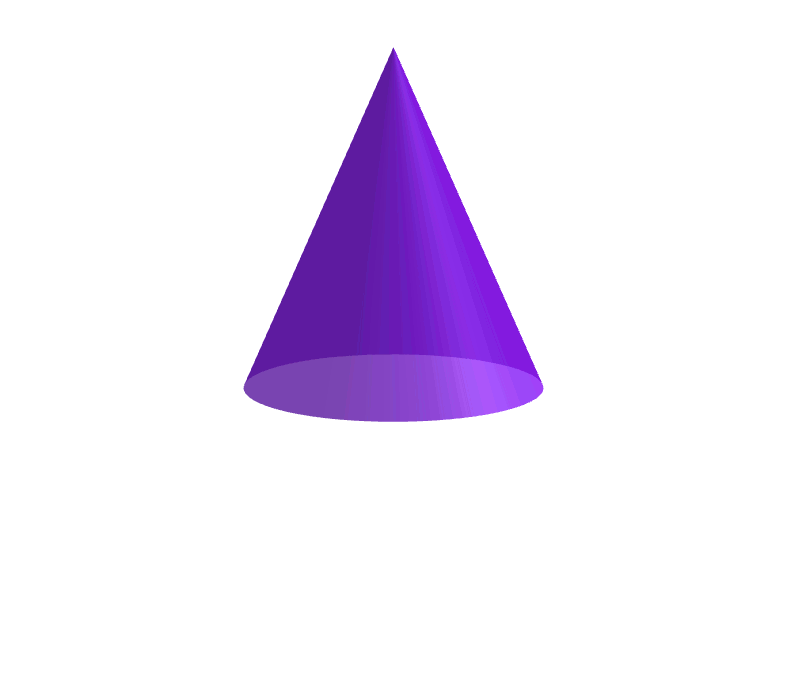
El área del cono es por tanto la suma del área del círculo de la base más el área del sector circular. Se puede calcular cnon la fórmula:
$\mbox{Área} =\mbox{área base}+\mbox{área sector} = \pi \cdot r^2 +\pi \cdot r \cdot g = \pi \cdot r \cdot (r+g)$
Ejemplo:
Calcula el área y el volumen de este cono que mide 8 cm de alto, su radio mide 6 cm y su generatriz 10 cm.
$\mbox{Volumen}=\dfrac{1}{3}\cdot \pi \cdot 6^2 \cdot 8 = 288 \pi \approx 904.78 \ cm^3$
$\mbox{Área cono}=\pi \cdot 6^2 +\pi \cdot 6 \cdot 10 =36 \pi + 60 \pi =96 \pi \approx 301.59 \ cm^2$
Esfera
Una esfera es el que cuerpo que se obtiene al girar un semicírculo sobre su diámetro.
Una esfera tiene la propiedad de que todos los puntos que la forman están a la misma distancia (radio) de un punto interior que se llama centro.
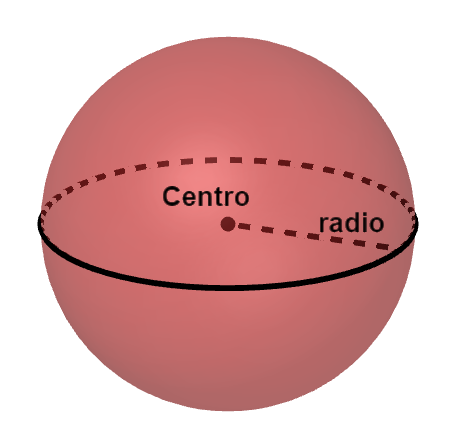
Hay multitud de ejemplos de esfera, una pelota, una canica, ...
El volumen de una esfera es igual a cuatro tercios del producto de pi por el radio al cubo.
$V=\dfrac{4}{3} \cdot \pi \cdot r^3$
La esfera no tiene desarrollo plano.
El área de una esfera es igual al cuádruple del producto de pi por el radio al cuadrado.
$A=4\cdot \pi \cdot r^2$
Es decir, el área de la esfera es igual al área de cuatro circunferencias con el mismo radio que la esfera.
Ejemplo:
Calcula el volumen y el área de esta esfera de radio 9 mm.
.png)
$V = \dfrac{4}{3} \cdot \pi \cdot r^3 =\dfrac{4}{3} \cdot \pi \cdot 9^3 =108\pi \approx 339.29\ mm^3$
$A=4\cdot \pi \cdot r^2=A=4\cdot \pi \cdot 9^2=364 \pi \approx 1017.88 \ mm^2$
Kardia dice ¡Qué curioso!
Los sólidos platónicos son poliedros en los que todas sus caras son polígonos regulares iguales, es decir, todas sus caras son triángulos equiláteros, cuadrados, pentágonos regulares, ...
El nombre de 'sólidos platónicos' viene de que el filósofo y matemático griego Platón, en su libro "Timeo" otorgó un papel destacado a estos polígonos regulares asociándolos a los elementos primarios de la naturaleza, en cada uno de ellos verás a qué elemento se asociaban.
Solo hay 5 sólidos platónicos que son:
Tetraedro
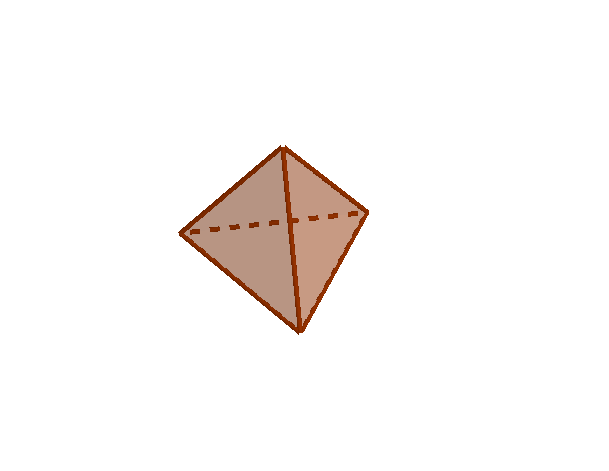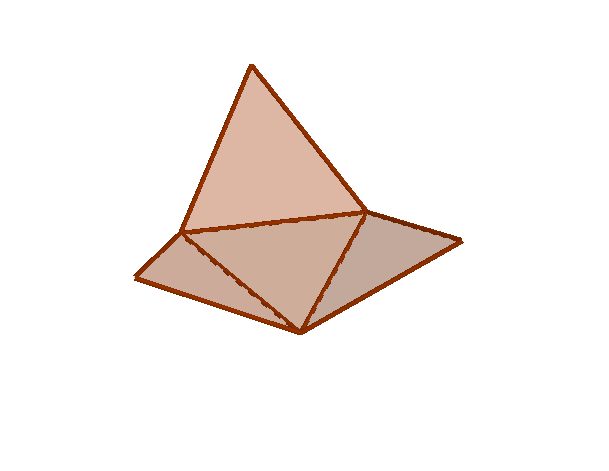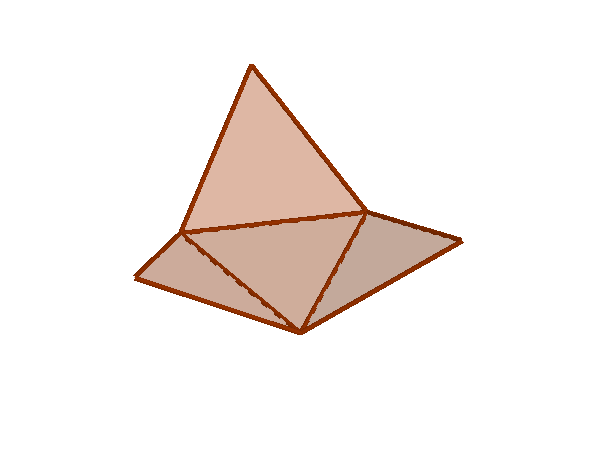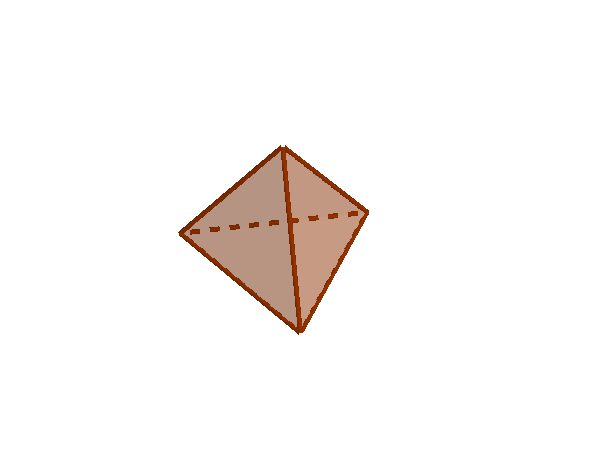
Características del tetraedro:
- 4 caras, todas son triángulos equiláteros.
- 4 vértices.
- 6 aristas
Platón asociaba el tetraedro con el fuego.
Cubo 
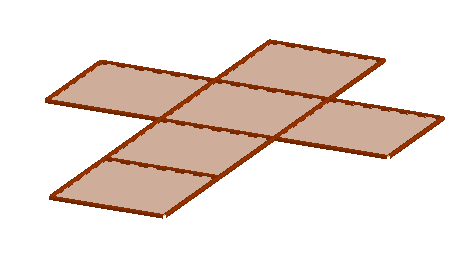
Observando el poliedro se pueden distinguir:
- 6 caras, todas ellas cuadradros.
- 8 vértices
- 12 aristas
El cubo se asociaba con la tierra.
Octaedro
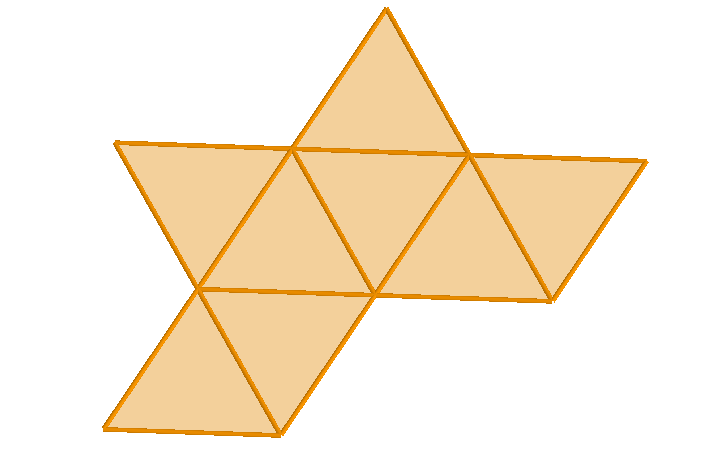
Características del octaedro:
- 8 caras, todas son triángulos equiláteros.
- 6 vértices
- 12 aristas
El octaedro era el aire.
Dodecaedro
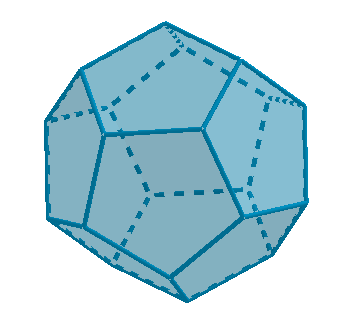
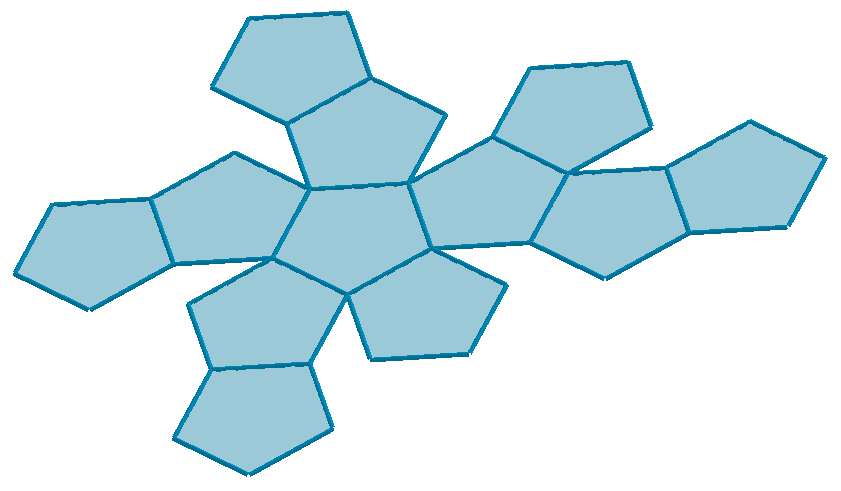
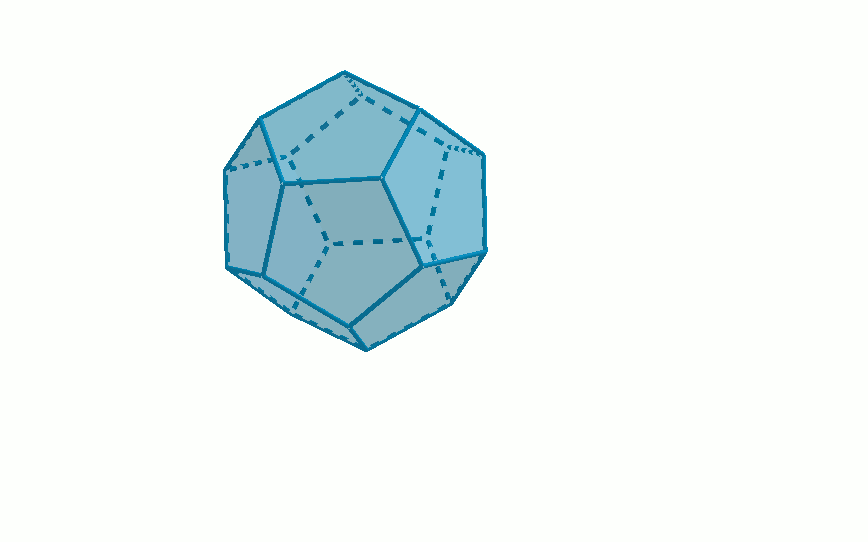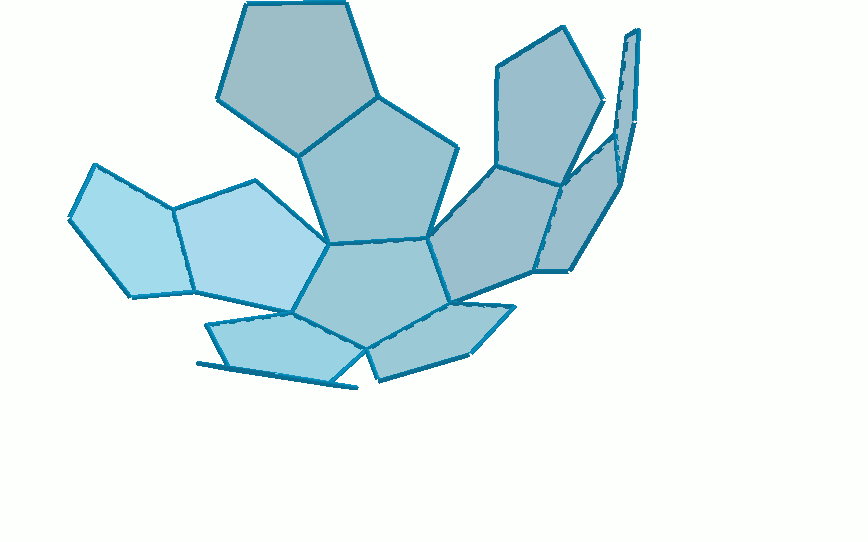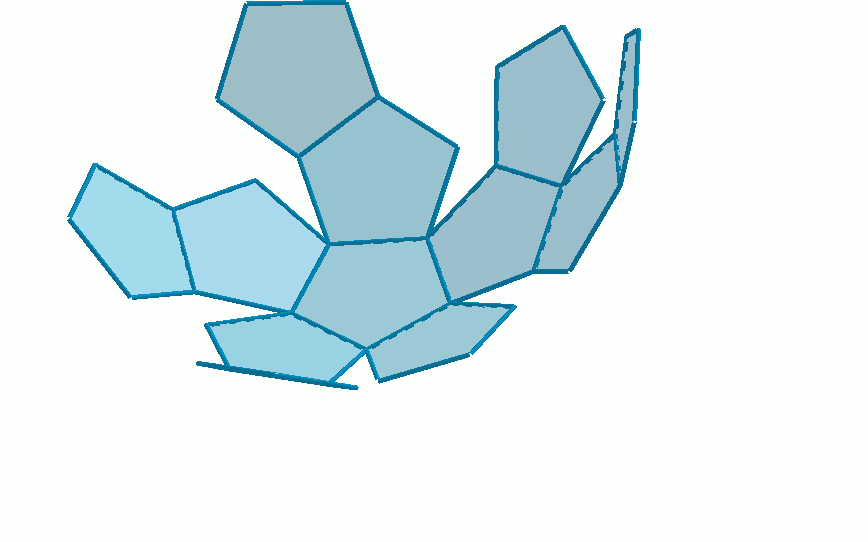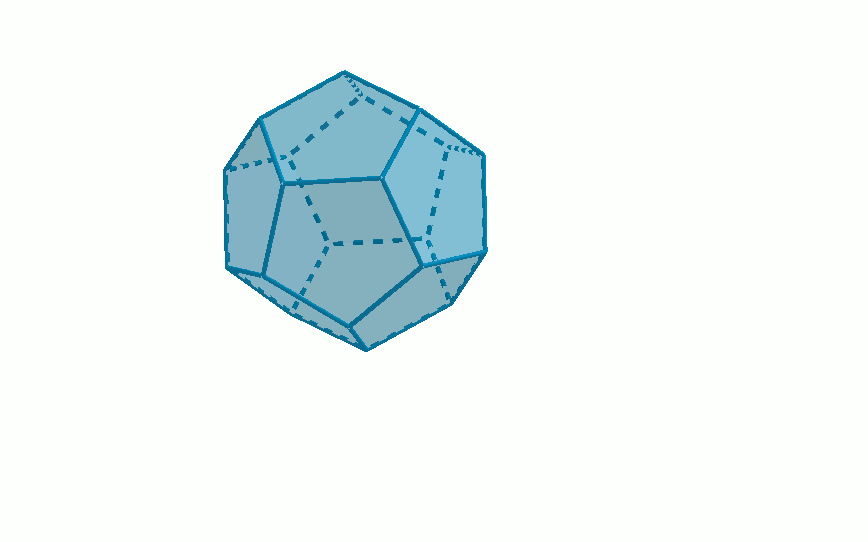
Características del dodecaedro:
- 12 caras, todas son pentágonos regulares.
- 20 vértices
- 30 aristas
Para Platón el dodecaedro era el quinto elemento, creía que formaba los cuerpos celestes, se asociaba al cosmos.
Icosaedro
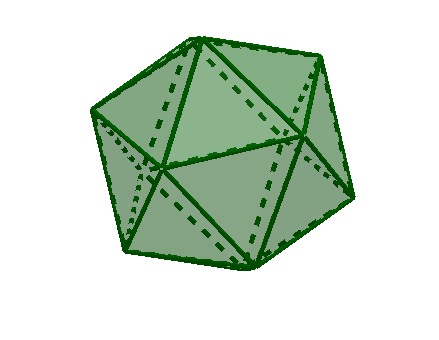
Características del icosaedro:
- 20 caras, todas son triángulos equiláteros.
- 12 vértices.
- 30 aristas
Platón asociaba el icosaedro al agua.
Comparativa
| Caras | Vértices | Aristas | |
| Tetraedro | 4 | 4 | 6 |
| Cubo | 6 | 8 | 12 |
| Octaedro | 8 | 6 | 12 |
| Dodecaedro | 12 | 20 | 30 |
| Icosaedro | 20 | 12 | 30 |
Observa que C+V=A+2
Donde C son las caras, V los vértices y A las aristas
4. Pasamos a la acción
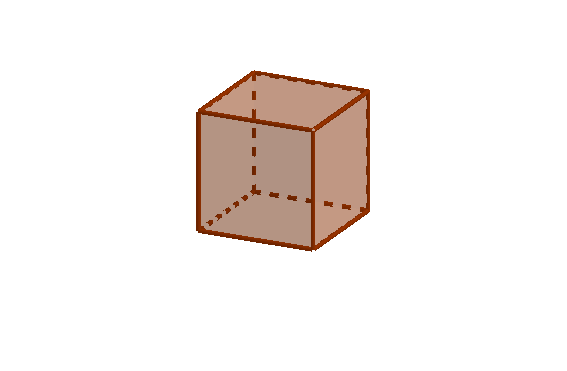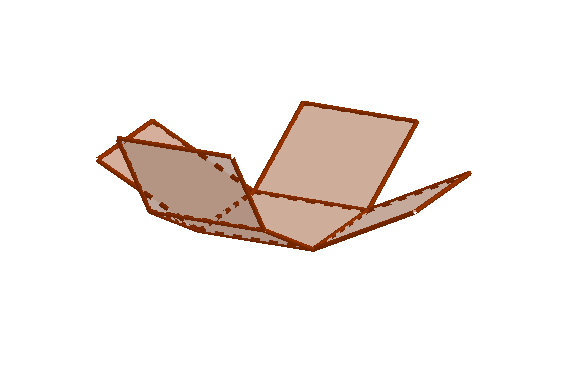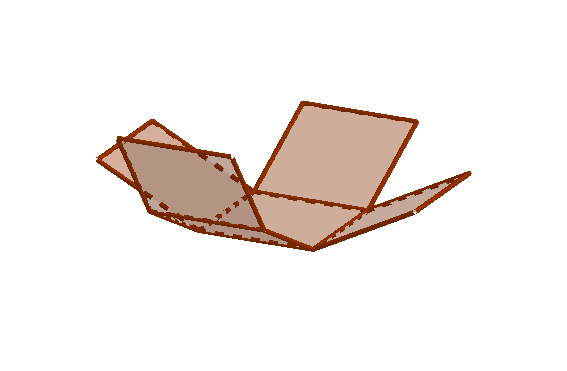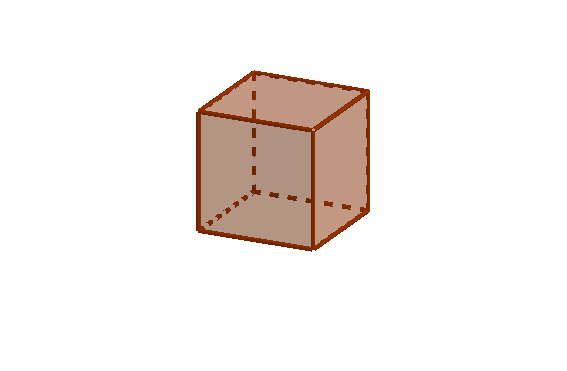
Ahora que conoces los cuerpos geométricos y la forma de calcular su volumen y área vas a empezar a trabajar con ellos.
Para la empresa de mensajería los más importantes son los ortoedros, porque la mayoría de paquetes tienen esa forma.
Opción A: Volumen el prisma y de la pirámide
Has visto que la fórmula para calcular el volumen de un prisma y de una pirámide es muy parecida, el volumen de una pirámide es un tercio del volumen de un prisma con la misma base y la misa altura.
$\mbox{Volumen prisma} = \mbox{área base} \cdot \mbox{altura}$
$\mbox{Volumen pirámide} =\dfrac{1}{3} \mbox{área base} \cdot \mbox{altura}$
En esta actividad vas a construir un prisma pentagonal y una pirámide pentagonal con la misma base y la misma altura y vas a comprobar esa relación.
Imprime este documento, recorta y construye los cuerpos geométricos. Sigue las instrucciones y observa como para llenar el prisma tienes que llenar tres veces la pirámide.
Opción B: Identifica los cuerpos geométricos
Ahora toca recordar todo lo que has visto antes. Realiza la siguiente actividad recordando los cuerpos geométricos, su desarrollo plano y la fórmulas de su volumen y de su área.
Si lo prefieres en papel descarga este documento.
Opción C: Calculando áreas y volúmenes
En la empresa de mensajería es muy importante el cálculo de áreas y volúmenes de los paquetes, que son cuerpos geométricos, sobre todo, ortoedros.
Practica, realizando todos los cálculos en tu libreta, calculando el volumen y área de los siguientes cuerpos geométricos.
Opción D: Diseña paquetes
Vas a diseñar y construir tus primeros envases para paquetes.
Como sabes, la mayoría de paquetes que se transportan en una empresa de mensajería son ortoedros. Esto es así, entre otras cosas, porque se pueden a
pilar muy fácilmente.
Para construir los paquetes de esta actividad vas a necesitar cartulinas de distinto tamaño, los más usuales son A4, A3 y 50x65 cm.
Diseña, recorta y construye un ortoedro grande y dos iguales más pequeños de forma que los dos más pequeños juntos encajen encima del grande, como le ocurre a los paquetes que tiene la mujer de la imagen debajo de la mano.
Opción E: Cilindro y esfera
Si vas a realizar esta actividad es que ya dominas el trabajo con áreas y volúmenes de los cuerpos geométricos.
En esta actividad va a ser un poco más teórica.
Dada una esfera de radio R, ¿cuáles son las dimensiones, radio y altura, del cilindro más pequeño en el que cabe la esfera?
A partir de la fórmulas del volumen del cilindro y la esfera, encuentra la relación que existe entre los volúmenes de una esfera y el menor cilindro capaz de contenerlo.
Motus dice Toc, toc…
¿Has hablado contigo mismo para resolver esta actividad?
No, no eres raro. Es muy frecuente que cuando estamos trabajando hablemos en silencio con nosotros mismos.
Es una forma de comprender mejor lo que hacemos y de buscar soluciones a las tareas o actividades.
De hecho, te aconsejo que lo hagas con mucha frecuencia porque te ayudará a:
- Recordar algunos pasos que necesites para realizar la actividad.
- Hacerte preguntas para entender mejor la información.
- Animarte a terminar la actividad, mantenerte concentrado…
- Saber cómo te sientes ante la actividad
Habla contigo mismo y aprenderás mejor.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0