Triángulo

Un triángulo es polígono que tiene tres lados.

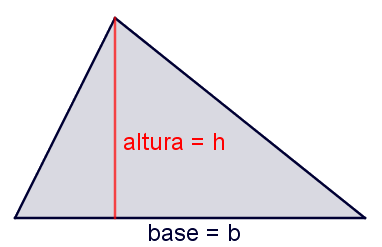
El área de un triángulo es igual al producto de la base por su altura dividido entre dos.

$A=\dfrac{b\cdot h}{2}$

La altura de un lado es la distancia de ese lado al vértice opuesto.

Ejemplo:

Vamos a calcular el área del siguiente triángulo:

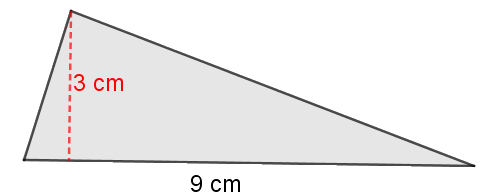
$A=\dfrac{\mbox{base}\cdot \mbox{altura}}{2}=\dfrac{9\cdot 3}{2}=\dfrac{27}{2}=13.5 \ cm^2$

Cuadrado

Un cuadrado es un polígono de cuatro lados que tiene todos los lados y todos los ángulos iguales.

El área de cuadrado es igual al lado al cuadrado.

$A=l^2$

Ejemplo:

Vamos a calcular el área del siguiente cuadrado:

$A = \mbox{lado}^2 = 4^2 = 16 \ cm^2$

Rectángulo

Un rectángulo es un polígono de cuatro lados que tiene los cuatro ángulos iguales.

El área de un rectángulo es igual a base por altura.

Es decir, el área de un rectángulo es el producto de los dos lados distintos.

$A = b \cdot h$

Ejemplo:

Vamos a calcular el área del siguiente rectángulo:

$A = \mbox{base}\cdot \mbox{altura} = 5\cdot 3 =15 \ cm^2 $

Rombo

Un rombo es un polígono que tiene cuatro lados iguales.

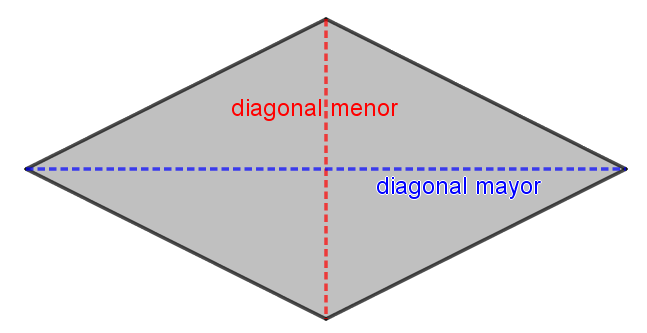
El área de un rombo es igual al producto de las diagonales dividido entre dos.

Se suele expresar, área del rombo igual a diagonal mayor por diagonal menor dividido entre dos.

$A =\dfrac{D\cdot d}{2}$

Una diagonal es el segmento que une dos vértices opuestos.

Ejemplo:

Vamos a calcular el área del siguiente rombo:

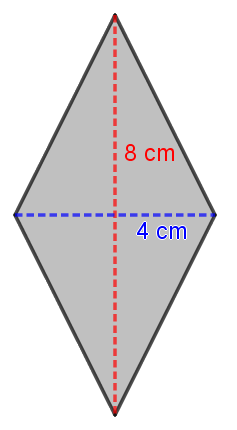
$A=\dfrac{\mbox{Diagonal mayor}\cdot \mbox{diagonal menor}}{2}=\dfrac{8\cdot 4}{2}=\dfrac{32}{2}=16 \ cm^2$

Paralelogramo

Un paralelogramo es un polígono de cuatro lados que tiene dos pares de lados paralelos.

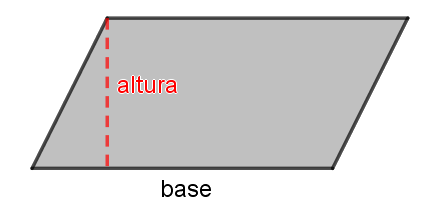
El área de un paralelogramo es igual al producto de la base por su altura.

$A=b\cdot h$

La altura sobre un lado es la distancia de ese lado al lado paralelo.

Ejemplo:

Vamos a calcular el área de este paralelogramo:

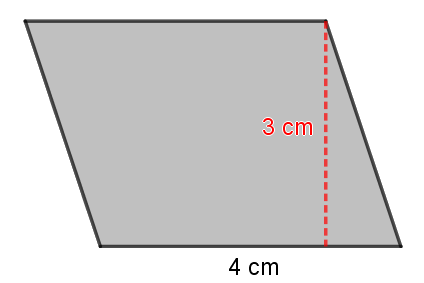
$A=\mbox{base}\cdot \mbox{altura} = 4 \cdot 3 =12 \ cm^2$

Trapecio

Un trapecio es un polígono de cuatro lados que tiene dos lados paralelos.

El área de un trapecio es igual a la suma de las dos bases, multiplicada por la altura y dividida entre dos.

Se suele expresar, área del trapecio igual la base mayor más base por menor, por altura entre dos.

$A=\dfrac{(B+b)\cdot h}{2}$

Las bases son los dos lados paralelos y la altura la distancia entre ellos.

Ejemplo:

Vamos a calcular el área del siguiente trapecio:

$A=\dfrac{(\mbox{Base mayor}+\mbox{base menor})\cdot \mbox{altura}}{2}=\dfrac{(4+2)\cdot 3}{2}=\dfrac{6\cdot 3}{2}=\dfrac{18}{2}=9 \ cm^2 $

Polígono regular

Un polígono regular es el que tiene todos sus lados y todos sus ángulos iguales.

El área de un polígono regular es igual al producto de su perímetro por el apotema dividido entre dos.

$A=\dfrac{P\cdot ap}{2}$

El perímetro es la suma de todos sus lados. Como todos los lados son iguales se puede calcular multiplicando lo que mide un lado por el número de lados.

El apotema es la distancia del centro del polígono a un lado.

Ejemplo:

Calcula el área del siguiente heptágono regular:

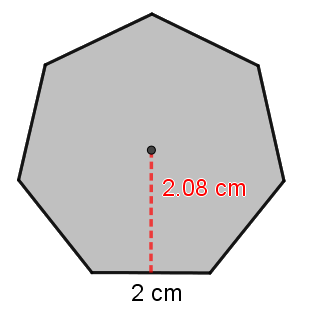
$\mbox{Perímetro} = \mbox{lado}\cdot \mbox{número de lados}=2\cdot 7=14 \ cm$

$A=\dfrac{\mbox{Perímetro}\cdot \mbox{apotema}}{2}=\dfrac{14\cdot 2.08}{2}=\dfrac{29.12}{2}=14.56 \ cm^2$

Círculo

Un círculo es la región del plano contenida dentro de una circunferencia.

Una circunferencia de centro C y radio R es el conjunto de puntos cuya distancia a C es R.

Es decir, la circunferencia es la línea exterior y el círculo lo que hay dentro.

El área de un círculo es igual al producto del número pi por el radio al cuadrado.

$A=\pi r^2$

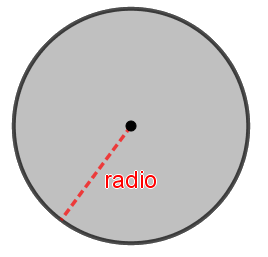
Ejemplo:

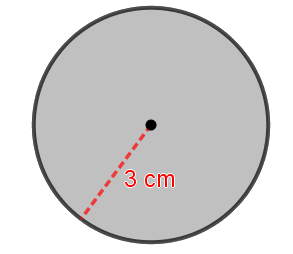
Vamos a calcular el área de este círculo:

$A=\pi \cdot \mbox{radio}^2=\pi \cdot 3^2 =\pi \cdot 9 \approx 28.27 \ cm^2$