Diccionario
Contigua

Extracción




Ya estamos casi a punto para poder empezar el proyecto final.
Antes queremos darte un par de herramientas que te ayudarán a contabilizar mejor los casos totales y favorables de cada situación.
Estamos hablando de los diagramas de árbol, que ya los has trabajado y además es una de las partes previas que tienes que desarrollar en el reto final.
También las tablas de doble entrada, son de gran utilidad para recoger y analizar la información obtenida de cada experimento aleatorio.
Estas herramientas serán fundamentales para elaborar el informe que presentaremos a la empresa de moda.
¡Ánimo!
Ya estamos casi a punto para poder empezar el proyecto final.
Antes queremos darte un par de herramientas que te ayudarán
a contabilizar mejor los casos totales y favorables de cada situación.
Estamos hablando de los diagramas de árbol,
que ya los has trabajado
y además es una de las partes previas
que tienes que desarrollar en el reto final.
También las tablas de doble entrada,
son de gran utilidad para recoger
y analizar la información obtenida de cada experimento aleatorio.
Estas herramientas serán fundamentales
para elaborar el informe que presentaremos a la empresa de moda.
¡Ánimo!

Podríamos llamar Técnicas de conteo a aquellas herramientas matemáticas que nos permite conocer de forma rápida las agrupaciones que se pueden realizar con los diferentes elementos de un conjunto.
Por ejemplo, ¿Cuántas banderas diferentes de tres franjas podemos hacer con cinco colores distintos? o ¿ De cuántas formas distintas podemos agrupar nuestros libros de lengua, matemáticas y biología?
También, en el caso de experimentos compuestos, puede ser necesario utilizar técnicas adecuadas para conocer el espacio muestral.
Gracias a las técnicas de conteo, podemos responder a estas preguntas de forma rápida y eficaz.
A continuación veremos algunas técnicas básicas de conteo.
Empezaremos por un caso sencillo, un experimento en el que se combinan dos experimentos sencillos.
En este caso, utilizaremos las tablas de doble entrada. Para que lo comprendas mejor, será mejor poner un ejemplo.
Supón que lanzamos dos monedas a la vez ¿qué posibles resultados podemos obtener?
En el primer lanzamiento tenemos dos posible resultados: (cara, cruz)=$\{(c\}$ o $\{+\}$. Empezamos construyendo la tabla:
| Cara | ||
| No cara |
En el segundo lanzamiento, el resultado también es: (cara, cruz)=$\{c\}$ o $\{+\}$. La tabla nos queda:
| Cara | No cara | |
| Cara | ||
| No cara |
El espacio muestra se construye rellenando la tabla.
| Cara | No cara | |
| Cara | (c,c) | (c,+) |
| No cara | (+,c) | (+,+) |
El espacio muestral será: $E=\{(c,c),(c,+),(+,c),(+,+)\}$
En la fase "Más y más caracteres", trabajaste con los diagramas de árbol.
Vamos a utilizarlos ahora para el cálculo de probabilidades.
Cuando combinamos más de dos experimentos sencillos,
tenemos que usar la técnica de diagrama de árbol.
Vamos a ver en qué consiste con un ejemplo.
Tenemos una urna con bolas de colores azul, rojo.
El experimento consiste en hacer tres extracciones .
¿Cuál sería el espacio muestral?
El espacio muestral estaría formado por ocho sucesos: $E=\{(A,A,A),((A,A,R),(A,R,A),(A,R,R),(R,A,A),(R,A,R),(R,R,A),(R,R,R)\}$

Podríamos llamar Técnicas de conteo
a aquellas herramientas matemáticas que nos permite conocer
de forma rápida las agrupaciones que se pueden realizar
con los diferentes elementos de un conjunto.
Por ejemplo,
¿Cuántas banderas diferentes de tres franjas
podemos hacer con cinco colores distintos?
¿ De cuántas formas distintas podemos agrupar nuestros libros
de lengua, matemáticas y biología?
También, en el caso de experimentos compuestos,
puede ser necesario utilizar técnicas adecuadas
para conocer el espacio muestral.
Gracias a las técnicas de conteo,
podemos responder a estas preguntas de forma rápida y eficaz.
A continuación veremos algunas técnicas básicas de conteo.
Tablas de doble entrada.
Empezaremos por un caso sencillo,
un experimento en el que se combinan dos experimentos sencillos.
En este caso, utilizaremos las tablas de doble entrada.
Para que lo comprendas mejor, será mejor poner un ejemplo.
Supón que lanzamos dos monedas a la vez
¿qué posibles resultados podemos obtener?
En el primer lanzamiento tenemos dos posible resultados:
(cara, cruz)={(c} o {+}.
Empezamos construyendo la tabla:
| Cara | ||
| No cara |
En el segundo lanzamiento, el resultado también es: (cara, cruz)=$\{c\}$ o $\{+\}$. La tabla nos queda:
| Cara | No cara | |
| Cara | ||
| No cara |
El espacio muestra se construye rellenando la tabla.
| Cara | No cara | |
| Cara | (c,c) | (c,+) |
| No cara | (+,c) | (+,+) |
¿Cómo utilizar las tablas de contingencia y los diagramas de árbol para calcular probabilidades?
En las siguientes pestañas vas a ver dos ejemplos que te enseñarán como utilizar estas herramientas en el cálculo de probabilidades.
Retomemos el ejemplo de lanzar dos dados y sumar las puntuaciones,
los diferentes sucesos que se pueden dar,
se recogen fácilmente en una tabla de doble entrada.
Observa:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
a) ¿Cuál es el espacio muestral de este experimento aleatorio?
¿Cuántos sucesos elementales forman el espacio muestral?
Como puedes observar, al realizar la tabla, estamos recogiendo todos los posibles resultados del experimento, es decir, estamos obteniendo el espacio muestral.
$E=\{2,3,3,4,4,4,5,5,5,5,6,6,6,6,6,7,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9,10,10,10,11,11,12\}$
Está formado por 36 sucesos elementales.
b) Escribe los sucesos $A=Obtener\;suma\;par$ $B=Obtener\;suma\;nº primo$ $C=Obtener\;suma\;mayor\;que\;5$.
Los sucesos pedidos son:
$A=\{2,4,6,8,10,12\}$ $B=\{2,3,5,7,11\}$ $C=\{6,7,8,9,10,11,12\}$
c) Calcula las siguientes probabilidades: $P(A)$,$P(B)$,$P(C)$.
Suceso $A$, hay 6 casos favorables de un total de 36, por tanto, según la ley de Laplace: $P=\dfrac{6}{36}=\dfrac{1}{6}\approx0,17$
Suceso $B$, hay 5 casos favorables de un total de 36, por tanto, según la ley de Laplace: $P=\dfrac{5}{36}=\approx0,14$
Suceso $C$, hay 7 casos favorables de un total de 36, por tanto, según la ley de Laplace: $P=\dfrac{7}{36}=\approx0,19$
Considera una urna que contiene 4 bolas de color azul y 6 bolas de color rojo.
Vamos a hacer dos extracciones, devolviendo en cada una de ellas la bola extraída a la urna.
a) Dibuja un diagrama de árbol que represente la situación.
b) Denominamos al suceso "sacar bola azul" mediante $A$ y al suceso "sacar bola roja" por $R$.
Determina las siguientes probabilidades:
a) El diagrama de árbol que representa la situación del ejercicio sería:
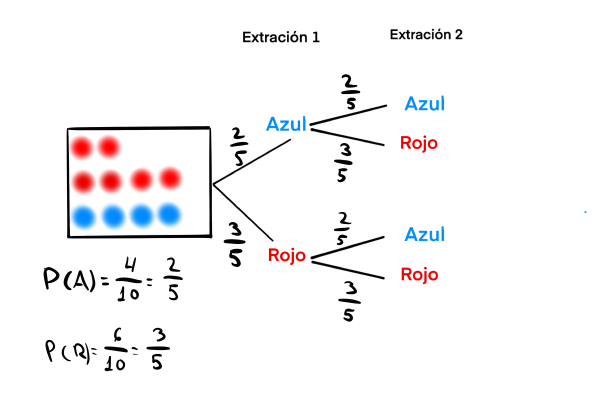
Observa como sobre cada rama está indicada la probabilidad de cada suceso elemental.
b) Fíjate bien en que los sucesos de los que hay que calcular la probabilidad en cada caso, están en ramas contiguas,
eso quiere decir que para hallar las probabilidades de los sucesos de esa rama,
habría que multiplicar en tres si las probabilidades de cada suceso elemental.
$P(1ªA y 2ª R)=\dfrac{2}{5}·\dfrac{3}{5}=\dfrac{6}{25}=0.24$
$P(1ªR y 2ª R)=\dfrac{3}{5}·\dfrac{3}{5}=\dfrac{9}{25}=0.36$
$P(1ªR y 2ª A)=\dfrac{3}{5}·\dfrac{2}{5}=\dfrac{6}{25}=0.24$
$P(1ªA y 2ª A)=\dfrac{2}{5}·\dfrac{2}{5}=\dfrac{4}{25}=0.16$

Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido)
¡Ánimo, que lo harás genial!

Vamos a integrar todo lo trabajado en contextos diferentes para ello te proponemos las siguientes actividades.
Presta mucha atención y realiza cada ejercicio con cuidado, ya que todo lo que vas a poner en práctica te será de utilidad en el reto final, que por cierto, está a la vuelta de la esquina.
Falso
Repasa las explicaciones de está página
Verdadero
Para reforzar esta idea, revisa el apartado: "Tablas de doble entrada y diagramas de árbol para calcular probabilidades".
Verdadero
Para reforzar esta idea, revisa el apartado: "Tablas de doble entrada y diagramas de árbol para calcular probabilidades".
Verdadero
Estudia el ejemplo puesto en el apartado "Calculo de probabilidades con diagramas de árbol"
Falso
Estudia el ejemplo con tabla de doble entrada de está página.
 Las reglas para desarrollar la carrera son las siguientes:
Las reglas para desarrollar la carrera son las siguientes:
Coge dos dados y juega varias veces, anotando en que puesto queda cada coche.
Responde a las siguientes preguntas:
a) ¿Qué coche ha ganado más veces? ¿Siempre ocurrirá lo mismo?
b) Explica qué ocurre con el coche 6.
c) ¿Por qué el coche 1 gana más que el cero?
1. Tira de nuevo los dados, y elabora una tabla de doble entrada en tu cuaderno con todos los posibles resultados del experimento de lanzar dos dados y restar los resultados.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
2.
Tira dos dados entre 100 y 150 veces, resta los resultados de cada tirada, y copia y completa la siguiente tabla:
| Resultado | Frecuencia absoluta | Frecuencia relativa |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Asigna una probabilidad aproximada a cada resultado.
 Vamos a ver qué opciones tienen los pilotos de formar su indumentaria.
Vamos a ver qué opciones tienen los pilotos de formar su indumentaria.
Como puedes ver en la imagen, hay cuatro colores disponibles.
Se trata de saber cuántas posibles combinaciones hay sin repetir color, es decir, si la camiseta es azul, el pantalón no puede ser de ese color.
a) Realiza en tu cuaderno un diagrama de árbol para averiguar las opciones disponibles.
b) ¿Cuál sería el espacio muestral de esta situación? ¿Cuántas opciones diferentes tiene el piloto para vestirse?
c) Calcula las probabilidades de cada una de las combinaciones.
¿Te has equivocado en algo al hacer la actividad?
Cuando queremos aprender algo, lo normal es equivocarse al principio. Fallar forma parte de aprender. ¿Recuerdas cuando montaste en bici por primera vez? ¿o cuando intentabas nadar en el agua? Seguro que al principio no fue fácil, pero cada vez que fallabas, lo intentabas de nuevo. Con cada fallo aprendemos del error y lo mejoramos para la vez siguiente.
Para aprender de tus errores sigue estos consejos:
1. Me doy cuenta de en qué parte he fallado.
2. Busco la forma de mejorar ese error.
3. Lo intento de nuevo.
4. Entiendo que el error es importante para aprender.
No lo olvides: cuando te equivocas una vez, aprendes para el siguiente intento.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0