Diccionario
Capital

Reinvertir




Has visto lo útiles que son las progresiones aritméticas para el cálculo del interés simple.
Pero esto no es suficiente, vas a estudiar ahora cómo el calculo de los intereses puede ir un poco más lejos.
Vas a utilizar las progresiones geométricas para aprender a manejar el interés compuesto.
Este cálculo será esencial para culminar con éxito el reto que te planteamos.
Has visto lo útiles que son las progresiones aritméticas
para el cálculo del interés simple.
Pero esto no es suficiente, ahora vas a estudiar
cómo el cálculo de los intereses
puede ir un poco más lejos.
Vas a utilizar las progresiones geométricas
para aprender a manejar el interés compuesto.
Este cálculo será esencial
para culminar con éxito el reto que te planteamos.
Ya eres un experto en sucesiones.
Así que vamos a intentar ampliar tus conocimientos.
Observa la siguiente secuencia de números:
\( 3,9,27,81,243,.......\)
Ya sabes que los términos de las sucesiones los nombramos de la siguiente manera: \( a_{1}=3 \), \( a_{2}=9 \), \( a_{3}=27 \), \( a_{4}=81 \), \(a_{5}=243 \).....
¿Sabrías calcular \( a_{7}\)?
Observa que cada término se obtiene del anterior multiplicando por tres.
Esto dicho de otra manera, es: si dividimos un término concreto entre el inmediatamente anterior, obtenemos tres.
\( \dfrac{a_{2}}{a_{1}}=\dfrac{9}{3}=3 ; \dfrac{a_{3}}{a_{2}}=\dfrac{27}{9}=3 ; \dfrac{a_{4}}{a_{3}}=\dfrac{81}{27}=3 ;\dfrac{a_{5}}{a_{4}}=\dfrac{243}{81}=3 \)
Una sucesión cuyos términos se obtienen multiplicando por una cantidad fija r, se llama Progresión Geométrica de razón r.
En nuestro ejemplo, tendríamos una progresión geométrica de razón 3.
Como puedes observar, los términos de una progresión geométrica son infinitos.
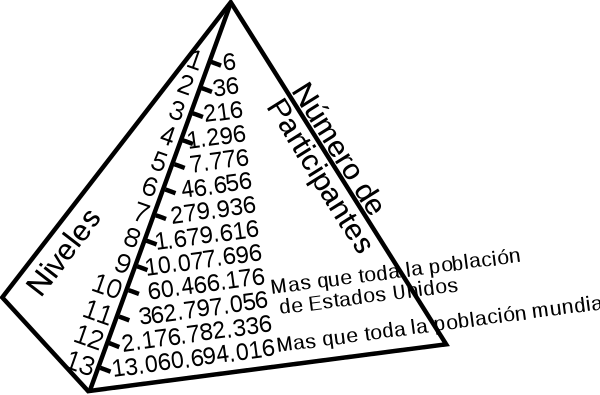
Partiendo del primer término de una progresión geométrica a1, y conociendo la razón, podemos obtener los siguientes términos.
\( a_{1}= a_{1}\)
\( a_{2}= a_{1}·r\)
\( a_{3}= a_{2}·r=a_{1}·r^2\)
Si generalizamos esta secuencia, obtenemos: \( a_{n}= a_{1}·r^{n-1}\)
A esta expresión le llamamos término general de la progresión, ya que conociendo el primer término y la razón, podemos obtener cualquier otro.
Vamos a aplicar el término general que acabamos de aprender para calcular términos de la progresión.
\(\rightarrow \) Calcular el quinto término de una progresión geométrica de \( r=-2\) y \(a_{1}=5\)
El término general sería: \(a_{n}=5·(-2)^{n-1}\) , luego el quinto término: \(a_{5}=5·(-2)^{5-1}=5·(-2)^4=5·16=80\)
\(\rightarrow \) Calcular el primer término de una progresión geométrica de razón 4, cuyo cuarto término es 128.
El término general de esta progresión sería: \(a_{n}=a_{1}·4^{n-1}\) , luego el cuarto término:
\(a_{4}=a_{1}·4^{4-1}=a_{1}·4^3\)
Se indica que el cuarto término es igual a 128, luego: \(a_{4}=a_{1}·4^3=128\) \(\rightarrow \) \(a_{1}·64=128\)
expresión de la que se puede calcular el primer término: \( \dfrac{128}{64}=2\)
La progresión tendría el siguiente término general: \(a_{n}=2·4^{n-1}\)
\(\rightarrow \) La razón de una progresión geométrica también puede ser una fracción. Estudia el siguiente ejemplo:
Calcula el quinto término de una progresión geométrica de razón \( r=\dfrac{1}{2}\) y \(a_{1}=32\)
El término general de esta progresión sería: \(a_{n}=32·\left( \dfrac{1}{2} \right)^{n-1}\)
El quinto término lo podemos calcular de la siguiente manera:
\(a_{5}=32·\left( \dfrac{1}{2} \right)^{5-1}=32·\left( \dfrac{1}{2} \right)^4=32·\dfrac{1}{2^4}=32·32·\dfrac{32}{16}=2\)
En determinadas situaciones, puede resultarnos útil conocer la suma de los primeros términos de una progresión geométrica, por ejemplo los 10 primeros términos, o los 6 primeros términos.
La expresión matemática para realizar este cálculo es: \(S_{n}=\dfrac{a_{1}·r^n-a_{1}}{r-1}\)
En el estudio del interés simple, hemos visto como los beneficios que se van obteniendo cada año, no se reinvierten.
¿Qué crees que ocurriría si al final de cada año, los beneficios obtenido se suma al capital y de este modo se reinvierte? Vamos a verlo.
El interés generado es el mismo que en el caso del interés simple: $i=0,05·8000=400$, luego el capital final después del 1º año es: $C_f=8000+400=8400 €$.
La diferencia viene ahora, para el 2º año, el capital inicial no es de $8000 €$, si no de $8400 €$. Por tanto el interés generado al final del 2º año es: $8400·0,05= 420 €$
El capital final después de ese 2º año sería: $C_f=8000·(1+0,05)^2=8400+420=8820 €$.
Puedes comprobar que el interés generado durante el 3º año sería: $8820 ·0,05=441 €$.
Por lo que el capital final en el 3º año es: $C_f=8000·(1+0,05)^3=9261 €$
Lo que está ocurriendo es que el capital final aumenta según una progresión geométrica en la que el primer término es $8000$ y la razón es $(1+0,05)$.
Se podría escribir que para el 3º año, el capital final es: $C_f=C_i·(1+0,05)^3$.
El capital final es: $C_f=C_i·(1+0,05)^4=8000·(1+0,05)^4=9724,05 €$
El capital final es: $C_f=C_i·(1+0,05)^5=8000·(1+0,05)^5=10210,26 €$


En general, la expresión para calcular el capital final de una determinada cantidad inicial $C_i$, sujeta aun interés compuesto de rédito $r$, durante un tiempo $t$ años, es:
$C_f=C_i·(1+\dfrac{r}{100})^t$
Si el tiempo va expresado en meses, la expresión sería:
$C_f=C_i·(1+\dfrac{r}{12·100})^{12·t}$
También se podría plantear capitalizar los intereses de forma trimestral, luego, como un año tiene 4 trimestres:
$C_f=C_i·(1+\dfrac{r}{4·100})^{4·t}$

En las siguientes actividades vas poner en practica lo que has aprendido sobre interés compuesto.
Te permitirá saber si esa reinversión te produce suficientes beneficios.
¡A por ello!
Completa la siguiente tabla aplicando un interés compuesto
IMPORTANTE: Introduce el resultado redondeando al número entero más cercano.
Al igual que hiciste con el interés simple, vamos a intentar averiguar de dónde viene la expresión matemática con la que calculamos el interés compuesto. Para ello sigue las siguientes indicaciones:
Imagina que tienes un capital C, y lo inviertes a un rédito r durante t años.
Calcula la sucesión formada por los capitales totales al final del primer año , al final del segundo año , al final del tercer año,......., al final del año t.
¿Qué tipo de sucesión es? ¿Cuál es la razón?
A partir de tus cálculos, ¿visualizas la expresión general?
Esta lista de cotejo te ayudará a comprobar si has deducido correctamente la fórmula.
¿Cuántas veces te has distraído al hacer la actividad?
Seguro que cuando estabas haciendo esta actividad ha ocurrido algo que te ha hecho parar. Puede que alguien pegase a la puerta, que el profe haya hablado con alguien, que hayas oído un ruido en la calle, que te hayas acordado de algo que hiciste ayer…
Cuando aprendemos estamos rodeados de cosas que nos pueden distraer. Al volver a la actividad te cuesta más trabajo centrarte.
Por eso es importante que aprendas a controlar tus distracciones. Te doy algunos consejos:
- Concéntrate bien en la actividad que tienes que realizar.
- Si tiene muchos pasos o es muy difícil, haz descansos cortos para descansar.
- Si te molesta lo que hay a tu alrededor trata de ver si puedes reducirlo: cierra las ventanas, pide silencio.
- Piensa que si te distraes tardarás más tiempo en terminar.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0