1. Nuestra ruta
Comenzaremos estudiando el principio de inclusión-exclusión para dos y tres conjuntos y, posteriormente, el principio de comparación que nos resultará de utilidad para acotar el número de elementos de un conjunto determinado.
MG1 - Situación de aprendizaje 1.1: Números y operaciones: Más coches que matrículas
6.2. Principios de inclusión-exclusión y de comparación
2. Debes saber
Principio de inclusión-exclusión: Nos permite calcular el cardinal de la unión de varios conjuntos a partir del cardinal de cada uno de ellos y de sus posibles intersecciones.
Para dos conjuntos A y B, este principio dice: card(A U B) = card(A) + card(B) - card(A ∩ B)
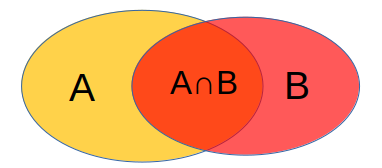
Justificación: A U B está formado por todos los elementos que pertenecen a A más todos los que pertenecen a B, pero los elementos comunes solo se escriben una vez. Cuando calculamos card(A) + card(B), los elementos de A ∩ B los estamos contando dos veces (están incluidos en el cardinal de A y también en el de B), es por eso que debemos restar card(A ∩ B).
Para entender cómo debemos aplicar este principio, veamos dos ejemplos.
3. Ejemplos
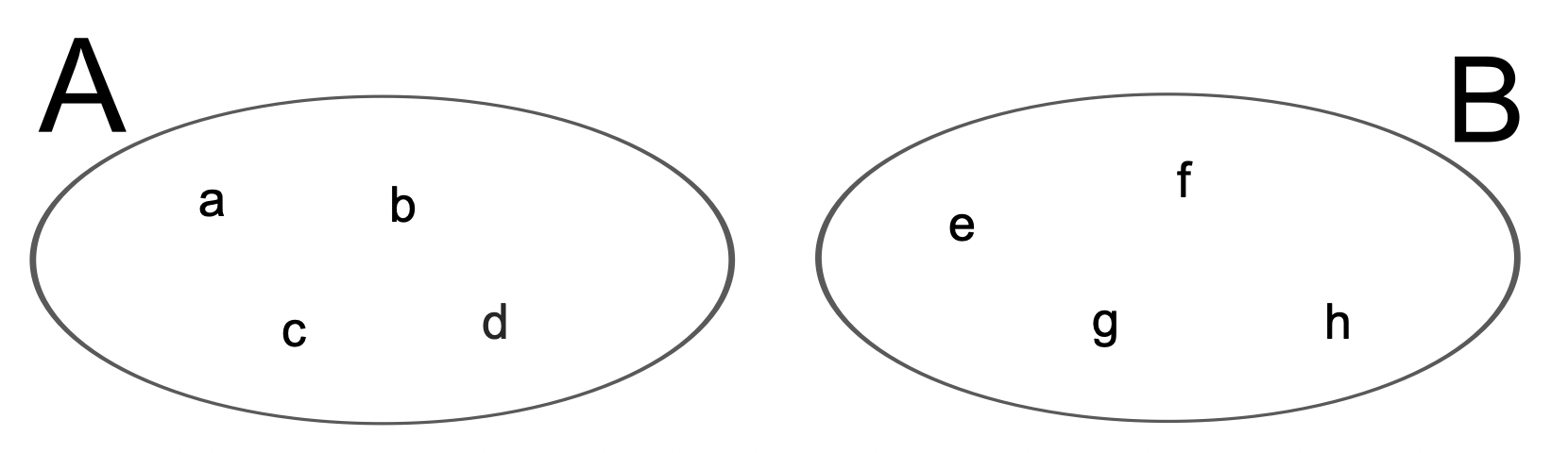
Ejemplo 1. Sean los conjuntos A = {a, b, c, d} y B = {e, f, g, h}. Tenemos que A U B = {a, b, c, d, e, f, g, h}
Como A y B son disjuntos, es decir, A ∩ B = Ø, implica que card(A ∩ B) = 0
Comprobamos que se cumple el principio
card(A U B) = card(A) + card(B) - card(A ∩ B), pues
card(A U B) = 8, card(A) = 4, card(B) = 4, card(A ∩ B) = 0 y obtenemos la igualdad 8 = 4 + 4 -0.
En general, si A y B son disjuntos siempre se cumple que card(A U B) = card(A) + card(B),
ya que card(A ∩ B) = 0.
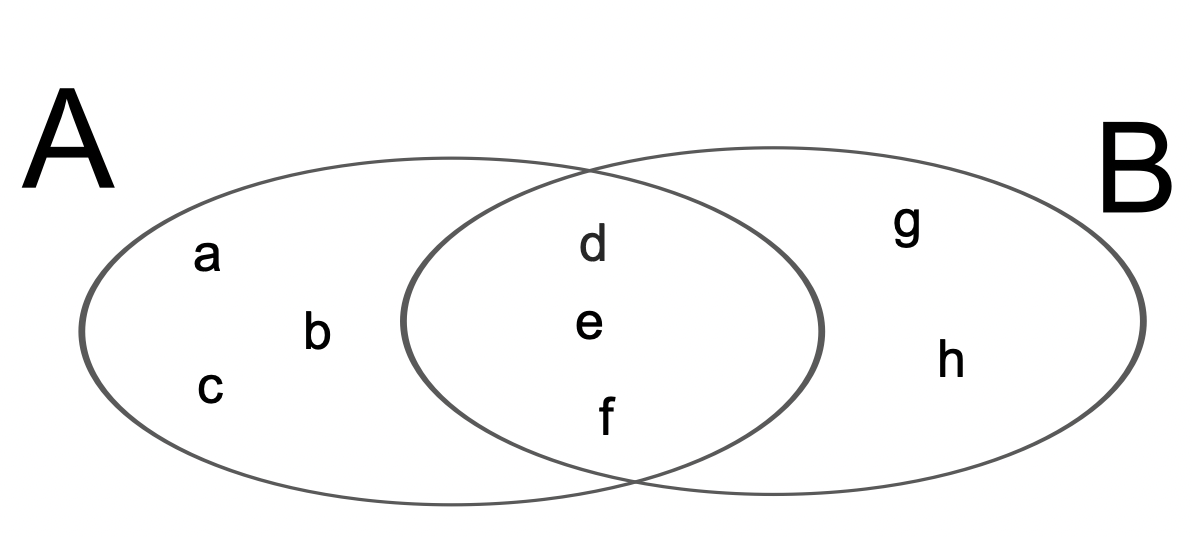
Ejemplo 2. Sean los conjuntos A = {a, b, c, d, e, f} y
B = {d, e, f, g, h}. Tenemos que
A U B = {a, b, c, d, e, f, g, h}
En este caso tenemos que A ∩ B = {d, e, f}
Debemos recordar que al calcular A U B, los elementos comunes {d, e, f} solo se escriben una vez.
Comprobamos que se cumple el principio
card(A U B) = card(A) + card(B) - card(A ∩ B), pues
card(A U B) = 8, card(A) = 6, card(B) = 5, card(A ∩ B) = 3 y obtenemos la igualdad 8 = 6 + 5 -3.
4. Caso práctico
En una encuesta realizada a un grupo de estudiantes sobre la utilización de redes sociales se encontró que 45 eran usuarios de Facebook, 52 de Instagram y 12 eran usuarios de ambas redes.
- ¿Cuántos estudiantes eran usuarios de Facebook o Instagram?
- ¿Cuántos estudiantes eran usuarios solo de Facebook?
- ¿Cuántos estudiantes eran usuarios solo de Instagram?
5. Ejercicio resuelto
En un grupo de 12 personas sabemos que 8 hablan inglés, 6 hablan francés y 4 ambos idiomas.
¿Podemos afirmar que todas hablan al menos uno de los dos idiomas?.
En el siguiente vídeo se explica la solución.
6. Resuelve y comprueba
Se preguntó a 50 personas sobre los deportes que practicaban, obteniéndose los siguientes resultados: 20 practican fútbol, 25 practican natación y 12 no practican ninguno de estos deportes. Con estos datos averigua:
1. El número de personas que practican alguno de dichos deportes.
2. El número de personas que practican fútbol y natación.
3. El número de personas que solo practican natación.
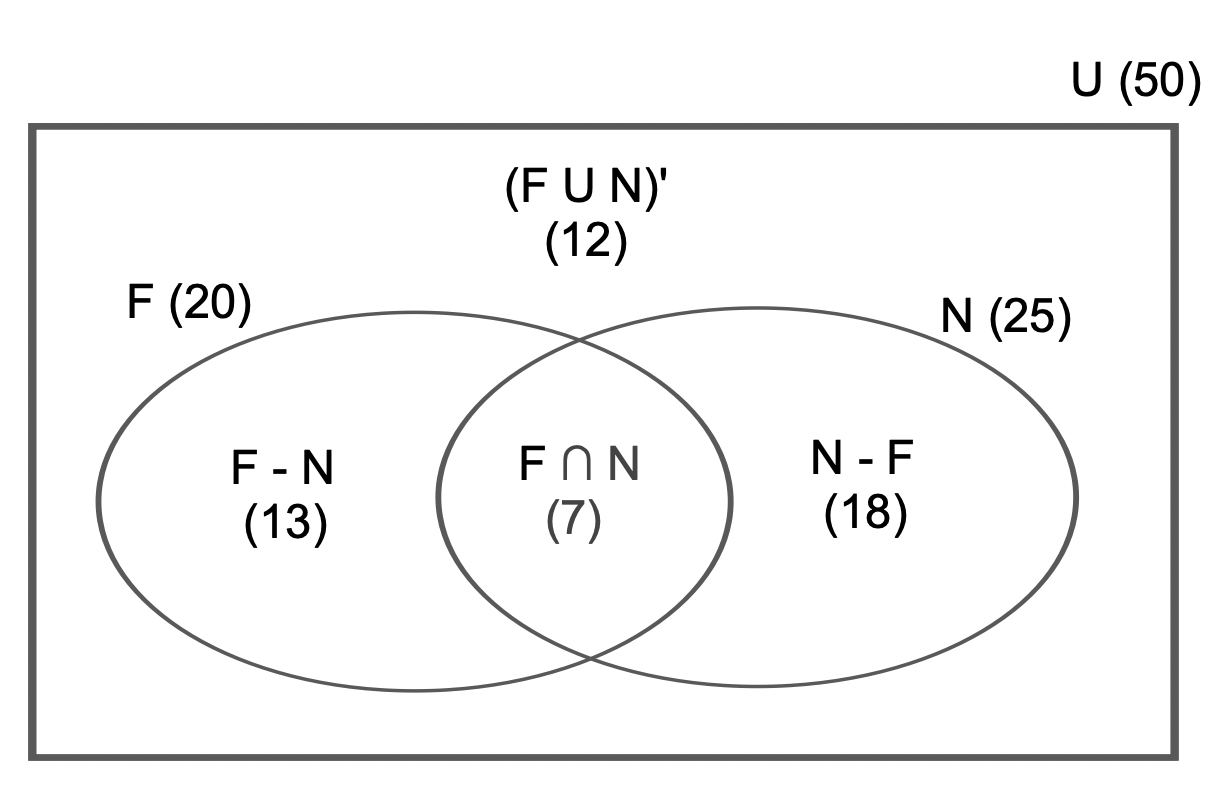
1. El conjunto universal está formado por las 50 personas que fueron preguntadas. Como hay 12 personas que no practica ninguno de los dos deportes, se deduce que hay 38 personas que practican alguno de ellos.
2. Nos piden que calculemos card(F ∩ N), siendo F el conjunto formado por las personas que practican fútbol y N el formado por las que practican natación. Aplicando el principio de inclusión-exclusión obtenemos:
card(F U N) = card(F) + card(N) - card(F ∩ N). Como card(F U N) = 38 por el apartado anterior, se tiene que 38 = 20 + 25 - card(F ∩ N). Despejando llegamos a que card(F ∩ N) = 20 + 25 - 38 = 7
3. El número de personas que practican solo natación viene dado por el número de personas que practican natación menos el número que practican natación y fútbol. Es decir, card(N) - card(F ∩ N) = 25 - 7 = 18.
En el siguiente diagrama de Venn podemos ver los cardinales de los diferentes conjuntos:
7. Debes saber
Principio de inclusión-exclusión para tres conjuntos A, B y C dice:
card(A U B U C) = card(A) + card(B) + card(C) - card(A ∩ B) - card(A ∩ C) - card(B ∩ C) + card(A ∩ B ∩ C)
Justificación: A U B U C está formado por todos los elementos que pertenecen a A junto con todos los que pertenecen a B y junto con todos los que pertenecen a C, pero los elementos comunes solo se escriben una vez. Cuando calculamos card(A) + card(B) + card(C) los elementos de A ∩ B, A ∩ C y B ∩ C los estamos contando dos veces, es por eso que debemos restar card(A ∩ B), card(A ∩ C) y card(B ∩ C). Al mismo tiempo, cuando calculamos card(A) + card(B) + card(C), los elementos de A ∩ B ∩ C los estamos contando 3 veces, pero como A ∩ B ∩ C es subconjuntos de A ∩ B, A ∩ C y B ∩ C y hemos restado sus cardinales, significa que card(A ∩ B ∩ C) lo hemos restado 3 veces también. Para que estos elementos queden incluidos en el cómputo total del cardinal de la unión debemos sumar su cardinal tal y como aparece en la expresión.
8. Ejercicio resuelto
Resolvamos un caso práctico en el que tenemos que aplicar este principio para tres conjuntos.
De los 130 alumnos de una academia de idiomas que imparte enseñanzas de inglés, francés y alemán, se sabe que 80 están matriculados en inglés, 60 en francés y 55 en alemán.
Además sabemos que algunos de ellos lo están en dos idiomas, concretamente hay 40 matriculados en inglés y francés, 15 en francés y alemán, y 20 en inglés y alemán.
- ¿Cuántos alumnos están matriculados en inglés, francés y alemán?
- ¿Cuánto se han matriculado en inglés y francés pero no en alemán?
En el siguiente vídeo puedes ver la solución explicada.
9. Resuelve y comprueba
Un entomólogo trabaja con 72 especies de insectos, de los cuales 34, 43 y 29 viven en ecosistemas de tipo A, B y C respectivamente. Sabiendo que 19 pueden vivir tanto en ecosistemas de tipo A como B, 11 en ecosistemas A y C, y 9 en ecosistemas B y C, obtener el número de especies que pueden estar presentes en los tres ecosistemas.
Calcular también el número de especies que pueden vivir en ecosistemas de tipo A y B pero que no pueden vivir en los de tipo C.
1. Aplicando el principio de inclusión-exclusión tenemos que: card(A U B U C) = card(A) + card(B) + card(C) - card(A ∩ B) - card(A ∩ C) - card(B ∩ C) + card(A ∩ B ∩ C).
Sabemos que card(A U B U C) = 72, card(A) = 34, card(B) = 43, card(C) = 29, card(A ∩ B) = 19, card(A ∩ C) = 11 y card(B ∩ C) = 9. Sustituyendo en la igualdad anterior obtenemos:
72 = 34 + 43 + 29 - 19 - 11 - 9 + card(A ∩ B ∩ C). Despejando llegamos a que card(A ∩ B ∩ C) = 5.
2. El cardinal que debemos calcular es card(A ∩ B) - card(A ∩ B ∩ C) = 19 - 5 = 14. Por tanto, 14 especies pueden vivir en ecosistemas de tipo A y B pero que no pueden vivir en los de tipo C.
10. Debes saber
Para finalizar, estudiamos el principio de comparación.
El principio de comparación dice: si A ⊆ B entonces card(A) ≤ card(B).
Ejemplo: si A = { a, e} y B = {a, e, i, o ,u}, tenemos que A ⊆ B y se cumple que card(A) ≤ card(B), pues 2 < 5.
11. Ejercicios de autoevaluación
En esta actividad debes indicar sin son verdaderas o falsas las siguientes afirmaciones.
Retroalimentación
Falso
A ∩ B es siempre un subconjunto de A (y también de B), es decir, A ∩ B ⊆ A. Por tanto, card(A ∩ B) ≤ card(A).
Retroalimentación
Falso
Sea C el conjunto formado por los asistentes que tomaron refresco de cola y N los que tomaron refresco de naranja. Aplicando el principio de inclusión-exclusión obtenemos que card(C U N) = card(C) + card(N) - card(C ∩ N). Sustituyendo los correspondientes cardinales obtenemos que
card(C U N) = 12 + 7 - 2 = 17. Es decir, 17 invitados tomaron refresco de cola o naranja. Luego asistieron más de 15 invitados.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0