1. Reflexiona
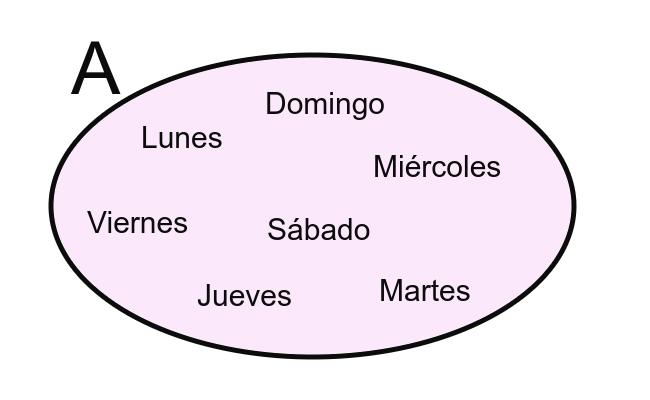
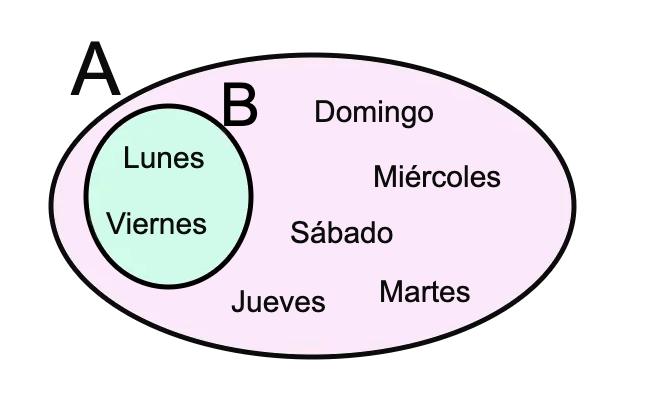
La capacidad de contar es una de las habilidades que adquirimos en los primeros años de nuestra vida y que contribuyen a la comprensión temprana de número. Al fin y al cabo, contar no es otra cosa que hacer corresponder, de manera ordenada, un número natural (1, 2, 3, etc) a cada uno de los objetos que deseamos contar. De ahí que los niños pequeños puedan resolver problemas sencillos que requieren la utilización de las operaciones elementales sumar, restar, multiplicar y dividir.
Sin embargo, debemos ser cuidadosos para evitar contar más de una vez un mismo objeto. Fíjate en el siguiente ejemplo.
SIN TIEMPO PARA LA ESCUELA
" Pero no tengo tiempo para la escuela", explicaba Eddie al preceptor. "Duermo ocho horas diarias que, sumadas, dan 122 días por año, suponiendo que cada día es de 24 horas. No hay clases los sábados ni los domingos, que suman 104 días por año. Tenemos 60 días de vacaciones de verano. Necesito tres horas diarias para comer... esto es más de 45 días al año. Y necesito al menos dos horas diarias de recreación... que suman más de 30 días al año." Eddie escribió estas cifras mientras hablaba, después sumó todos los días. La suma daba 361.
- Sueño (8 horas diarias) 122
- Sábados y domingos 104
- Vacaciones de verano 60
- Comidas (3 horas diarias) 45
- Recreación (2 horas diarias) 30
Total 361 días
"Ya ve", continuó Eddie; "eso me deja tan sólo cuatro días para estar enfermo y en cama, y ni siquiera he tomado en cuenta los siete feriados escolares que tenemos cada año". El preceptor se rascó la cabeza. "Algo no anda bien aquí", murmuró. Pero por más que se esforzó, no pudo encontrar nada equivocado en las cifras de Eddie."
Gardner, Martin (1986) Matemática para divertirse. Editorial Granica
¿Puedes explicar dónde está el error?