Correcto.
Sea E el conjunto formado por las etiquetas del primer tipo, es decir, E = {00, 01, 02,........, 98, 99} cuyo cardinal es 100
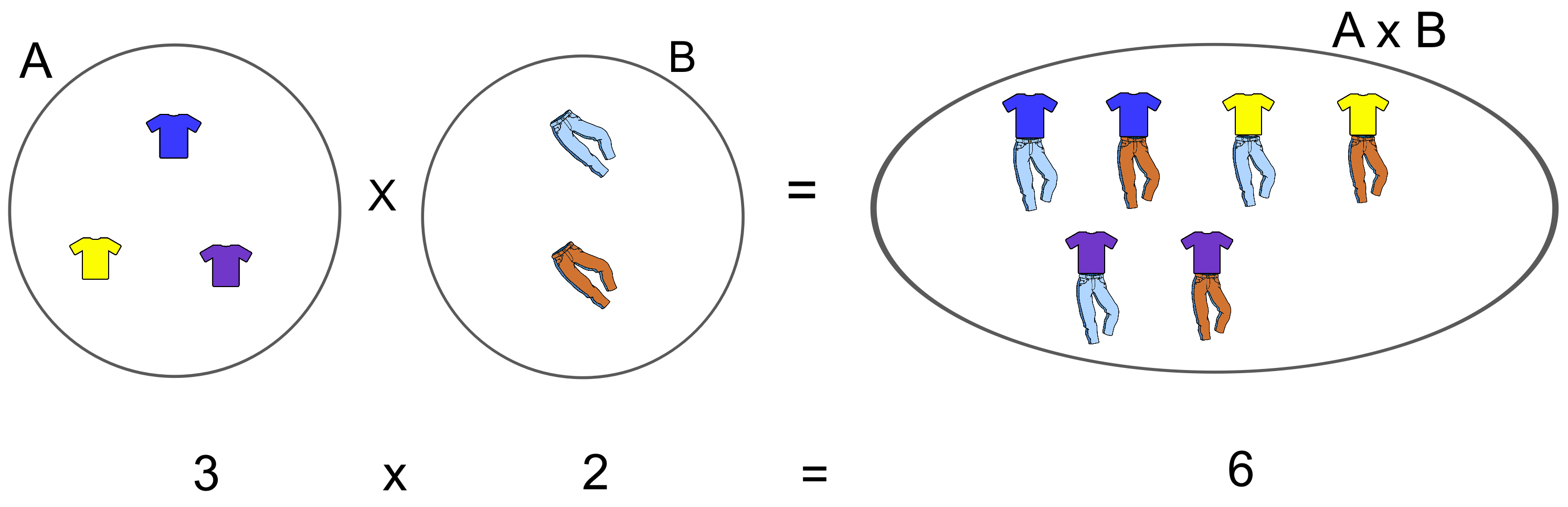
Sea F el conjunto formado por las etiquetas del segundo tipo, es decir, E = {A0, A1, A2,........, U8, U9} que se ha obtenido a partir de los conjuntos A = {a, e, i, o, u} y B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} mediante la operación producto de dos conjuntos F = A x B.
Sabemos que card(F) = card(A) x card(B) = 5 * 10 = 50.
Para determinar el número de etiquetas diferentes del segundo tipo que se pueden formar hemos utilizado el principio de multiplicación.
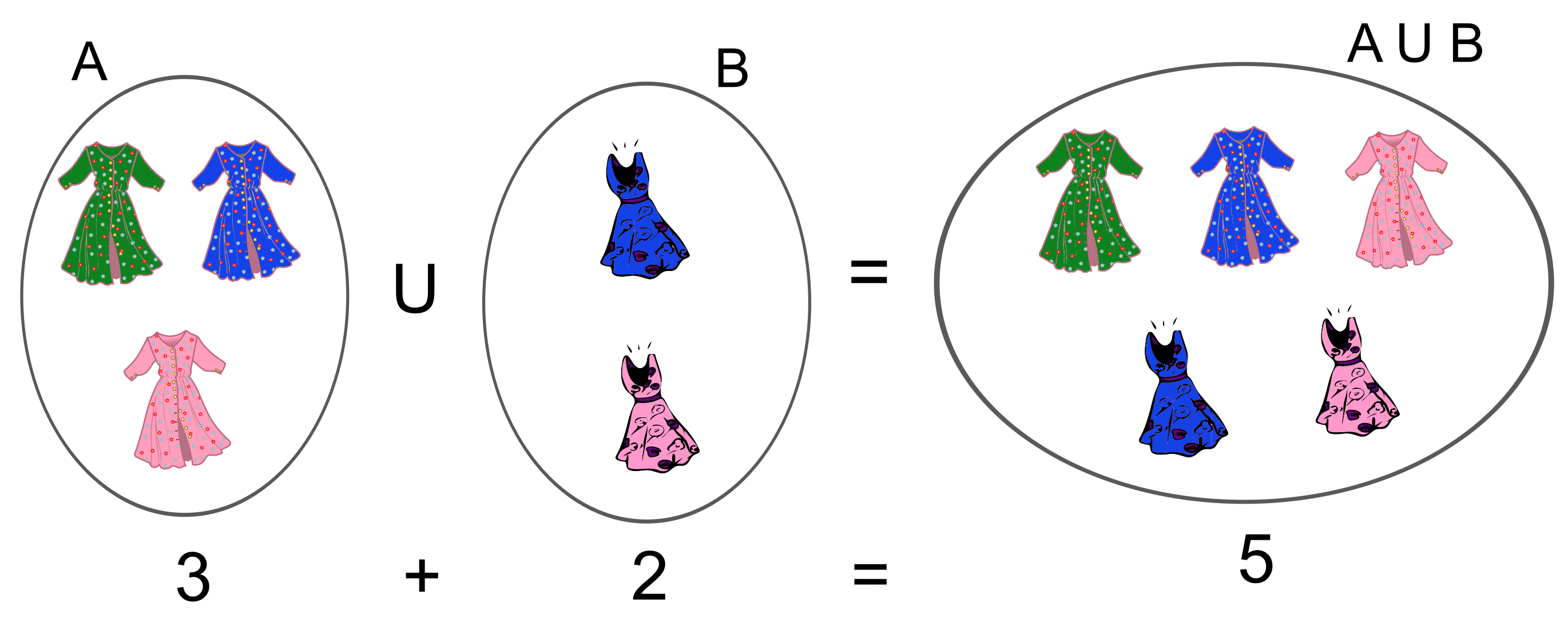
Finalmente, como cada envío lleva solo una etiqueta, ya sea del primer tipo o del segundo, significa que debemos tomar una etiqueta dentro del conjunto E U F.
Dado que las etiquetas del primer tipo y del segundo son todas diferentes entre sí (E y F son conjuntos disjuntos), tenemos que card(E U F) = card(E) + card(F) = 100 + 50 = 150, aplicando el principio de adición.
Por consiguiente, para determinar el número total de etiquetas disponibles hemos tenido que aplicar tanto el principio de multiplicación como el de adición.