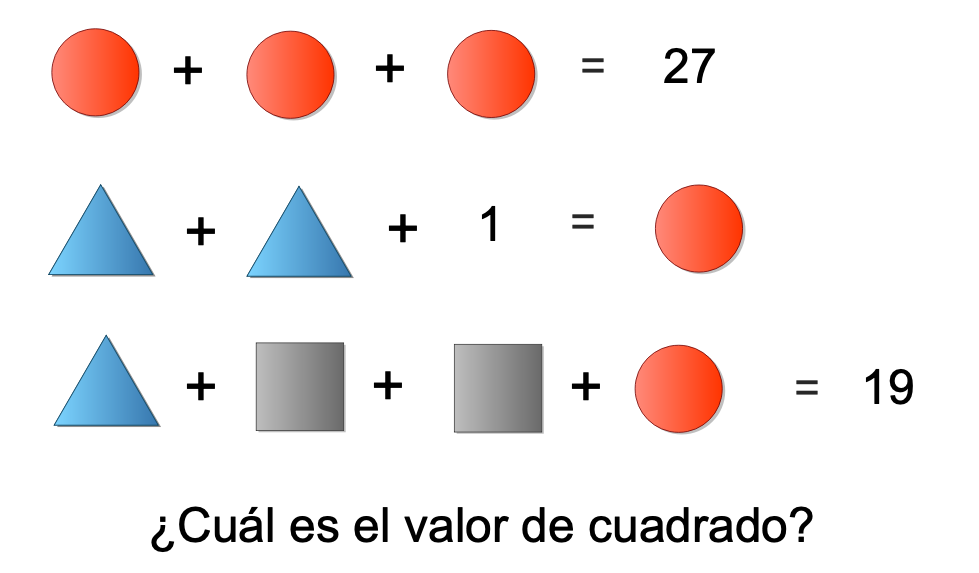
1. Lenguaje algebraico y expresiones algebraicas
El lenguaje algebraico es un sistema sistema de escritura y comunicación que se utiliza en el campo de las matemáticas. Se caracteriza por emplear símbolos, números y letras para representar cantidades y relaciones matemáticas de manera abstracta y general. Este sistema no sólo facilita la formulación y resolución de problemas matemáticos, sino que también actúa como un puente entre el lenguaje cotidiano y el matemático, permitiendo la conversión de situaciones reales o problemas a términos matemáticos. Las letras, dentro de este lenguaje, simbolizan variables o incógnitas, representando valores desconocidos.
Estos ejemplos ilustran cómo se efectúa esta traducción:
1. Lenguaje habitual: "La suma de dos números es igual a un tercer número."
Lenguaje algebraico: Sean x , y los dos números, y z el tercer número. La relación se expresa como x + y = z.
2. Lenguaje habitual: "El doble de la edad de una persona es cinco años más que la edad de otra persona."
Lenguaje algebraico: Si a representa la edad de la primera persona y b la de la segunda, la relación se expresa como 2a = b + 5.
3. Lenguaje habitual: "Un rectángulo tiene un largo que es tres veces su ancho."
Lenguaje algebraico: Si l es el largo y a el ancho del rectángulo, la relación se describe como l = 3a.
4. Lenguaje habitual: "Un número es igual al cuadrado de otro número menos dos."
Lenguaje algebraico: Si n es el primer número y m es el segundo, la relación se expresa como n = m2 - 2.
Las expresiones algebraicas son combinaciones de números, variables (letras que representan cantidades desconocidas o variables), y operaciones matemáticas como suma, resta, multiplicación y división.
Por ejemplo:
- Expresión lineal simple: 3x + 4. Esta expresión representa una suma donde 3x es el término variable y 4 es el término constante.
- Expresión cuadrática: x2 - 5x + 6. Aquí, x2 es un término cuadrático, -5x es lineal, y 6 es una constante.
- Expresión racional: 2x / (x + 1). Esta es una expresión fraccionaria donde el numerador es 2x y el denominador es x + 1.
- Expresión algebraica con varias variables: 5x-3xy2- 2x(y-1)2
El signo de multiplicar se sobreentiende delante de una letra o un paréntesis. Así, 5·x es equivalente a 5x, y 2·(x-6) es equivalente a 2(x-6).
Una expresión algebraica puede componerse de uno o más elementos llamados términos o monomios. Un conjunto de monomios sumados forma un polinomio. En cada monomio, las variables se conocen como la parte literal, mientras que el número que multiplica estas variables es el coeficiente.
Por ejemplo, en la expresión 3x, el coeficiente es 3 y la parte literal x. En -3xy2 el coeficiente es -3 y la parte literal xy2.
El grado del monomio es el exponente de su variable (también llamada indeterminada), en el caso en que haya más de una indeterminada, el grado será la suma de los exponentes de todas las indeterminadas.
Por ejemplo:
- En el monomio $4x^{2}$, el grado es dos, la única indeterminada es x y está elevada a dos.
- En el monomio $4xy$, el grado también es dos, porque x tiene de exponente uno e y también, la suma es dos.
- En el monomio $4x^{3}y^{2}$, el grado es cinco, es la suma de los exponentes de las indeterminadas: $3+2=5$.
El grado de un polinomio se determina por el grado más alto presente en sus monomios. Por ejemplo, x2 - 5x + 6 es un polinomio de grado 2 en la variable x. Si aparecen varias indeterminadas (variables), el grado del monomio será la suma de los exponentes de esas variables. Por ejemplo, el grado de -3xy2 es 3 en las variables x e y.
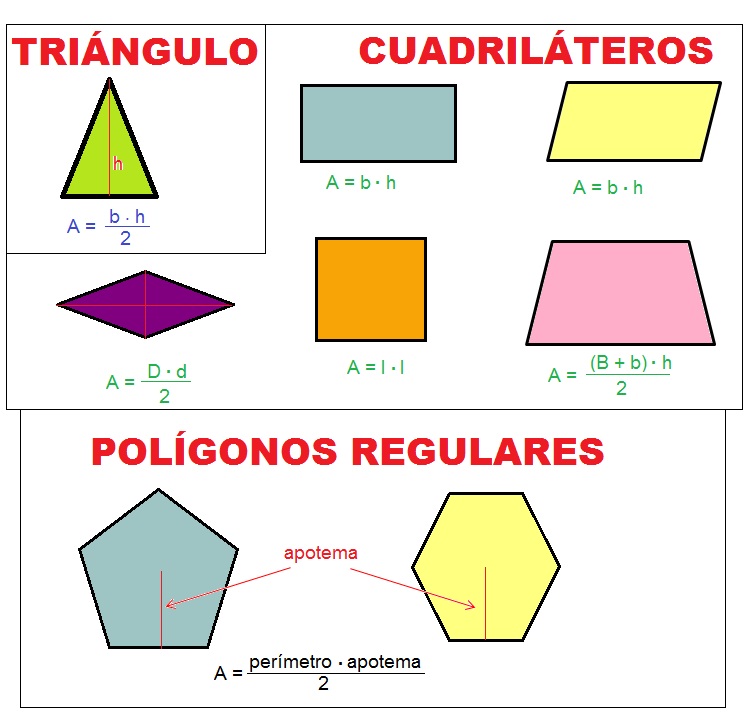
Las fórmulas relativas a figuras geométricas son excelentes ejemplos de expresiones algebraicas, ya que representan relaciones matemáticas que involucran figuras y formas geométricas.
El valor numérico de una expresión algebraica es el resultado que se obtiene al sustituir las variables de la expresión por valores numéricos específicos y realizar las operaciones indicadas.
Por ejemplo:
- Consideremos la expresión algebraica 2x+3. Si sustituimos x por 5, la expresión se convierte en 2⋅5+3. Realizando las operaciones, obtenemos 10+3=13. Por lo tanto, el valor numérico de 2x+3 cuando x=5 es 13.
- Supongamos que tenemos la expresión 3x2−2xy+4y−5. Para encontrar su valor numérico para x=2 e y=3, sustituimos estos valores en la expresión y obtenemos: 3(2)2−2(2)(3)+4(3)−5 = 7
- También calculamos valores numéricos cuando aplicamos fórmulas de geometría: la fórmula para el área de un círculo es A=πr2, donde r es el radio del círculo. Si sustituimos r por 4 cm, la fórmula se convierte en A=π⋅42=π⋅16. Si usamos aproximadamente 3.1416 para π, obtenemos A ≈ 3.1416⋅16 ≈ 50.2656 cm².