6. Resumen
1.- Resumen: Ejercicio por los cuatro métodos
Utiliza los cuatro métodos vistos en esta Situación de aprendizaje para resolver el siguiente Programa Lineal.
Maximizar la función $z=3x+4y$, sujeta a las siguientes restricciones:
$\left. \begin{array}{l} x \geq 0 \\ y \geq 0 \\ y\leq6 \\x+3y\leq19 \\ x+y\leq9 \\ 3x+y\leq21 \end{array} \right\} $
Método Analítico
Dado que se trata de un ejercicio no es necesario dar todos los pasos del protocolo de actuación visto en el punto 2 de esta situación de aprendizaje, los tres primeros pasos de este protocolo ya nos lo da el propio ejercicio, así que comenzamos en el punto 4:
$\left. \begin{array}{l} x \geq 0 \\ y \geq 0 \\ y\leq6 \\x+3y\leq19 \\ x+y\leq9 \\ 3x+y\leq21 \end{array} \right\} $
4) Graficar el recinto:Para cada inecuación obtenemos la ecuación cambien el signo de desigualdad por el de igualdad, tendremos entonces una linea recta que dando dos valores a una de las incógnitas (normalmente x) obtenemos el valor de la otra (normalmente y) y con ello un punto por el que pasa la recta y que dividirá el plano en dos semiplanos, uno válido y otro que no vale, que no verifica la desigualdad. Repetiremos este proceso con todas las desigualdades y obtendremos el recinto de soluciones factibles. Resumimos el proceso para este problema en la siguiente tabla:
| DESIGUALDAD | RECTA | PUNTO 1 | PUNTO 2 | COMPROBACIÓN |
| $x \geq 0$ | $x=0$ | $(0,0)$ | $(0,10)$ | Punto: $(2,0) \rightarrow 2\geq 0 \rightarrow \text{ Cierto}$ |
| $y \geq 0$ | $y=0$ | $(0,0)$ | $(10,0)$ | Punto: $(0,2) \rightarrow 2\geq 0 \rightarrow \text{ Cierto}$ |
| $y \leq 6$ | $y=6$ | $(0,6)$ | $(10,6)$ | Punto: $(0,0) \rightarrow 0\leq 6 \rightarrow \text{ Cierto}$ |
$x+3y \leq 19$ |
$x+3y = 19$ | $(1,6)$ | $(10,3)$ | Punto: $(0,0) \rightarrow 0\leq 19 \rightarrow \text{ Cierto}$ |
$x+y \leq 9$ |
$x+y = 9$ | $(9,0)$ | $(0,9)$ | Punto: $(0,0) \rightarrow 0\leq 9 \rightarrow \text{ Cierto}$ |
$3x+y \leq 21$ |
$3x+y = 21$ | $(7,0)$ | $(3,12)$ | Punto: $(0,0) \rightarrow 0\leq 21 \rightarrow \text{ Cierto}$ |
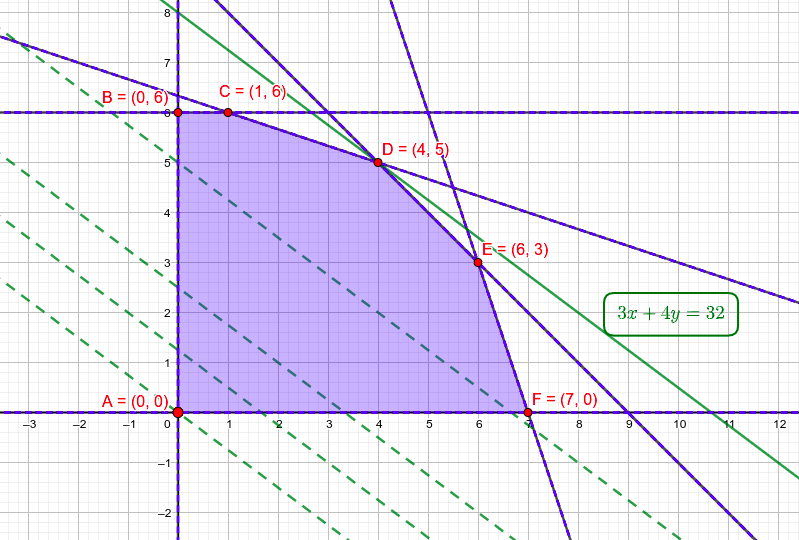
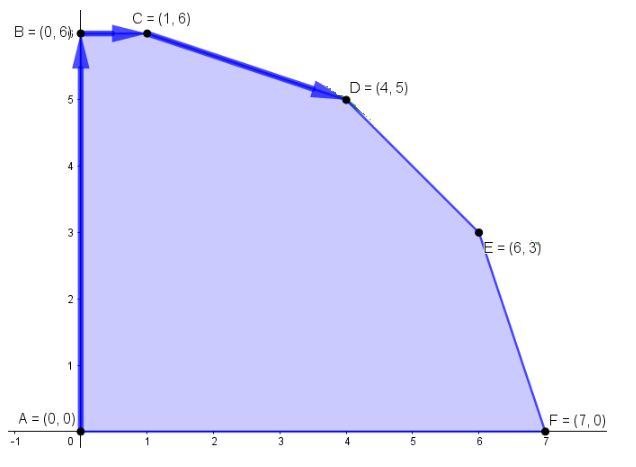
Con esta tabla podemos representar el recinto solución que resulta ser el siguiente, donde se ven ya los valores de los vértices que determinaremos en el apartado siguiente estudiando el corte entre cada dos rectas:
5) Identificar los vértices: Con geogebra solo tenemos que seleccionar el botón de intersección y las dos rectas en cuestión y el propio programa nos lo da, en papel o examen debemos resolver el sistema de dos ecuaciones con dos incógnitas que se obtiene al considerar cada pareja de rectas: Vamos a hacerlos paso a paso:
- Obtención del punto A: $\left. {\Large{x=0 \atop y=0}} \right\}$
como ya tenemos ambos valores de x e y en realidad ya tenemos el punto: $A:(0,0)$ - Obtención del punto B: $\left.{\Large{x=0 \atop y=6}}\right\}$
como ya tenemos ambos valores de x e y en realidad ya tenemos el punto: $B:(0,6)$ - Obtención del punto C: $\left.{\Large{y=6 \atop x+3y=19}}\right\}$
como ya tenemos que $y=6$ sustituimos en la segunda ecuación: $x+3·6=19 \rightarrow x=19-18 \rightarrow x=1 $
y por lo tanto el punto C es: $C:(1,6)$ - Obtención del punto D: $\left.{\Large{x+3y=19 \atop x+y=9}}\right\}$
En este caso debemos resolver el sistema, se puede hacer por el método de reducción, si restamos las dos ecuaciones:
$\begin{matrix} x & +3y & =19 \\ -x & -y & =-9 \\ \hline \text{ } & 2y & =10 \end{matrix} $
De donde: $2y=10 \rightarrow y=5 \rightarrow x+5=9 \rightarrow x=9-5 \rightarrow x=4 $ y por lo tanto el punto D es: $D:(4,5)$
- Obtención del punto E: $\left.{\Large{3x+y=21 \atop x+y=9}}\right\}$
En este caso debemos resolver el sistema, se puede hacer por el método de reducción, si restamos las dos ecuaciones:
$\begin{matrix} 3x & +y & =21 \\ -x & -y & =-9 \\ \hline 2x & \text{ } & =12 \end{matrix} $
De donde: $2x=12 \rightarrow x=6 \rightarrow 6+y=9 \rightarrow y=9-6 \rightarrow y=3 $ y por lo tanto el punto E es: $E:(6,3)$
- Obtención del punto F: $\left.{\Large{y=0 \atop 3x+y=21}}\right\}$
como ya tenemos que $y=0$ sustituimos en la segunda ecuación: $3·x+0=21 \rightarrow 3x=21 \rightarrow x=7 $
y por lo tanto el punto F es: $F:(7,0)$
6) Evaluación de la función objetivo en cada vértice: Sustituimos los valores de las coordenadas de cada vértice en la función objetivo:
$\left. \begin{array}{l} F_A=F(0,0)=3·0+4·0=0 \\ F_B=F(0,6)=3·0+4·6=24 \\ F_C=F(1,6)=3·1+4·6=27 \\ F_D=F\textbf{(4,5)}=3·4+4·5=\textbf{32} \\ F_E=F(6,3)=3·6+4·2=30 \\F_F=F(7,0)=3·7+4·0=21 \end{array} \right\} $
7) Selección de la solución óptima: A la vista de los resultados anteriores podemos concluir con la solución del ejercicio: El máximo se alcanza en el punto $(4,5)$ con un valor en la función objetivo de $32$.
El punto 8 tampoco es necesario porque es propio de un problema donde se explica el significado de los valores obtenidos en el apartado anterior.
Método Gráfico
El método gráfico coincide con el analítico en muchos de sus puntos, se difiere del visto en la pestaña anterior básicamente en el punto 6 donde lo que se hace es dibujar las diferentes rectas paralelas a la función objetivo básica $3x+4y=0$ e ir cambiando ese cero por valores más grandes para comprobar por cuál de los vértices del recinto salimos del mismo, ese vértice será el que nos informe del óptimo, sus coordenadas nos darán x e y del óptimo y el valor de k el máximo.
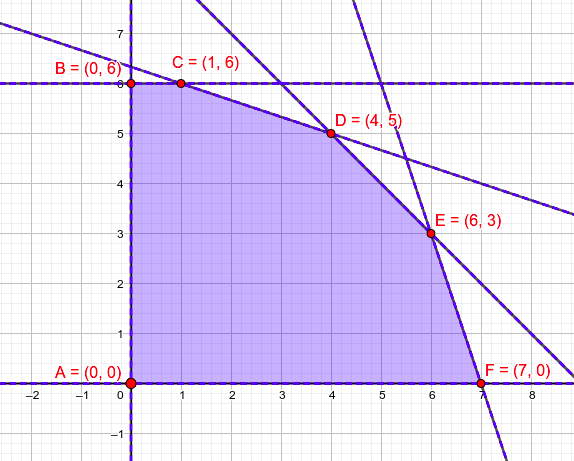
Por tanto todos los apartados anteriores son válidos para éste método salvo el 6 donde debemos hacer una gráfica como la que se aprecia en la siguiente imagen donde hemos ido dibujando rectas paralelas a la función objetivo (en verde discontinuo) hasta llegar a la que toca al último vértice del recinto que está dibujada en verde continuo y con su expresión en verde para tener el detalle del máximo.
Como puede verse el máximo es el mismo que en el método anterior, el punto $(4,5)$ y $z=32$, no tendría sentido que fuera diferente:
Método Solver
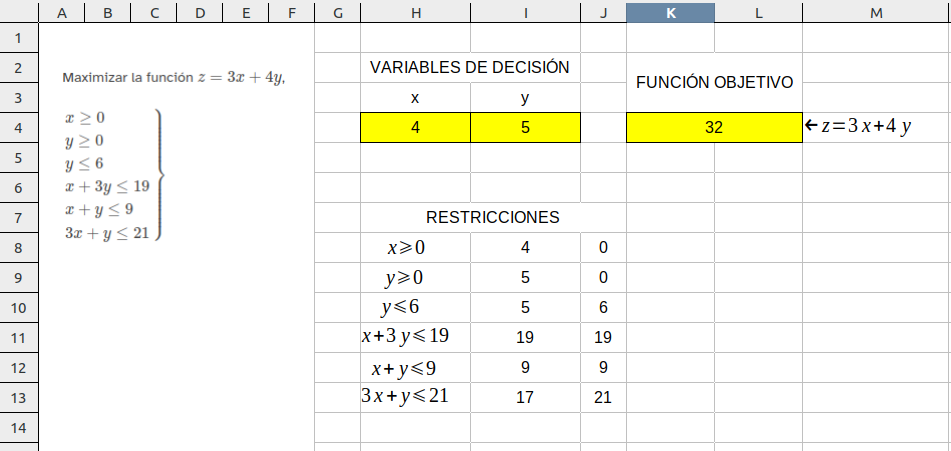
Para resolver este ejercicio por el método solver necesitamos introducir los datos en excel o en libre office. En este caso lo vamos a hacer en libre office y se explicarán con las imágenes capturadas y además tienes a tu disposición el documento de libre office en el siguiente enlace por si quieres ver como se han ido rellenando las diferentes celdas.
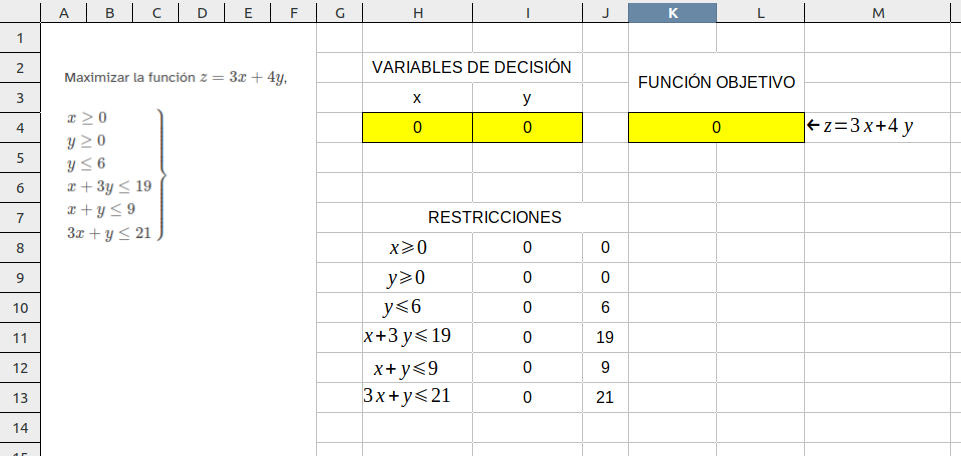
- Lo primero que hemos hecho ha sido introducir una imagen con los datos del problema a la izquierda para tenerlos a mano.
- Posteriormente hemos preparado la zona de las variables de decisión (en este caso x e y) tal como se ha explicado en los videos anteriores.
- Después el lugar para la función objetivo, escribiendo en el cero de la celda de fondo amarillo la expresión correspondiente, en nuestro caso =3*H4+4*I4
- El siguiente paso es escribir las restricciones, se han hecho por parte, se ha escrito la expresión completa, a su derecha el miembro izquierdo de la desigualdad y a la derecha el miembro derecho, para recoger esas expresiones en la tabla de la herramienta solver, como ejemplo citamos uno de los casos, en la celda I11 se ha introducido =H4+3*I4, mientras que en la siguiente celda J11 se ha introducido 19 que es el segundo miembro de la desigualdad.
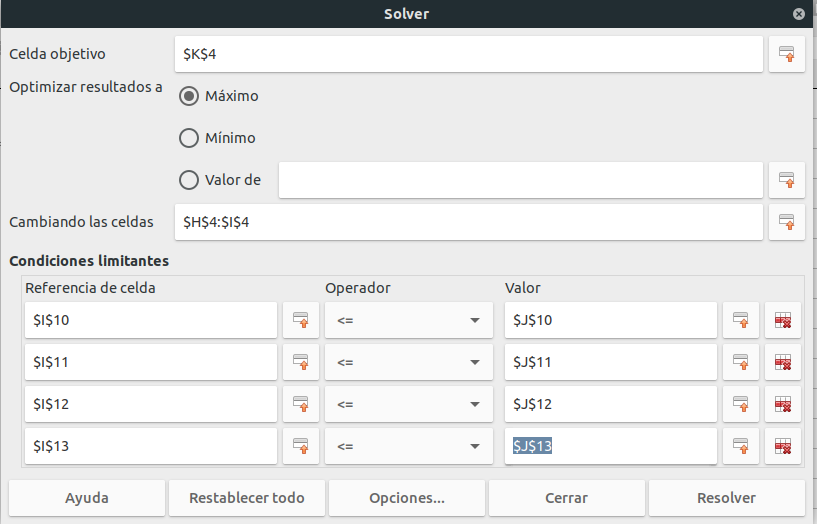
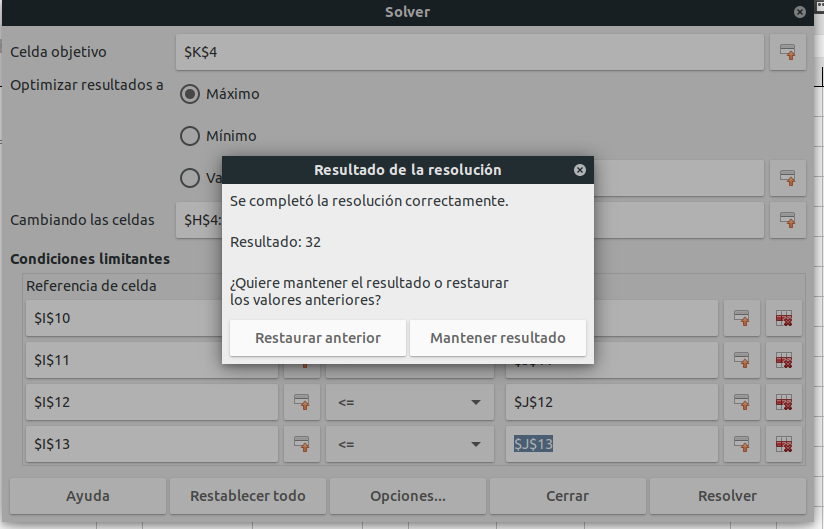
Una vez introducidos los datos en libre office tenemos que preparar la herramienta solver, introduciendo las celdas donde están la función objetivo, las variables de decisión y las restricciones, todo ello queda recogido en la siguiente imagen, recuerda que normalmente las expresiones triviales de $x\geq0$ e $y\geq0$ no son necesarias ponerlas. En las siguientes imágenes vemos como queda la tabla tras las introducción de los datos (Tabla 1) y el resultado o mensaje que da libre office tras aceptar:
Finalmente recogemos el resultado del problema resuelto que lógicamente vuelve a darnos el mismo valor que en los dos casos anteriores, nos fijamos en las celdas de fondo amarillo donde están las variables de decisión $(x,y)=(4,5)$ y el valor de la función objetivo: $z=32$
Método Simplex
El método simplex comienza transformando la función objetivo y las restricciones añadiendo variables de holgura para que las desigualdades se transformen en igualdades, así que eso es lo primero que haremos:
Maximizar la función $z=3x+4y$, sujeta a las siguientes restricciones:
$\left. \begin{array}{l} x \geq 0 \\ y \geq 0 \\ y \leq 6 \\x+3y\leq19 \\ x+y\leq9 \\ 3x+y\leq21 \end{array} \right\} $
Introducimos las variables de holgura $s_1, s_2, s_3, s_4 \geq 0$ para obtener la ecuaciones del sistema equivalente:
$\left. \begin{array}{l} x_1, x_2, s_1, s_2, s_3, s_4, \geq 0 \\ y+s_1=6 \\ x+3y+s_2=19 \\ x+y+s_3=9 \\ 3x+y+s_3=21 \end{array} \right\} $
Y la función objetivo quedará: $z3x+4y+ 0·s_1+0· s_2+0· s_3+0· s_4$
Establecemos como variables básicas de este sistema $(s_1, s_2, s_3, s_4)=(6,19,9,21)$ de este modo $(x,y)=(0,0)$ y la función objetivo a maximizar toma el valor $z_1=0$.
| Entrada $\rightarrow$ | $x$ | $y$ | $s_1$ | $s_2$ | $s_3$ | $s_4$ | Paso 1 | $\downarrow$ |
| $z$ | $-3$ | $-4$ | $0$ | $0$ | $0$ | $0$ | $z_1=0$ | Salida |
| $s_1$ | $0$ | $1$ | $1$ | $0$ | $0$ | $0$ | $6$ | $6\div 1=6$ |
| $s_2$ | $1$ | $3$ | $0$ | $1$ | $0$ | $$0$$ | $19$ | $19 \div3={\large{\frac{19}{3}}}$ |
| $s_3$ | $1$ | $1$ | $0$ | $0$ | $1$ | $0$ | $9$ | $9 \div1=9$ |
| $s_4$ | $3$ | $1$ | $0$ | $0$ | $0$ | $1$ | $21$ | $21 \div1=21$ |
En esta tabla anterior observamos que el coeficiente menor de z corresponde a la variable $y$ y que el valor del cociente entre el término independiente y el coeficiente de la variable que entra (última columna) más pequeño es el correspondiente a $s_1$, la variable $y$ sustituye a la variable $s_1$ como variable básica, cambiamos en la primera columna la variable $s_1$ por la variable $y$ y copiamos la fila correspondiente por la fila donde confluyen ambas variables (la segunda de la tabla anterior) pero divididos todos los números por el elemento de confluencia en este caso el $1$ de la celda que está de color verde en la tabla anterior, al dividir por cero la fila queda igual.
| $x$ | $y$ | $s_1$ | $s_2$ | $s_3$ | $s_4$ | Paso 1 | |
| $z$ | $-3$ | $-4$ | $0$ | $0$ | $0$ | $0$ | $z_1=0$ |
| $y$ | $0$ | $1$ | $1$ | $0$ | $0$ | $0$ | $6$ |
| $s_2$ | $1$ | $3$ | $0$ | $1$ | $0$ | $19$ | ${\large{\frac{19}{3}}}$ |
| $s_3$ | $1$ | $1$ | $0$ | $0$ | $1$ | $9$ | $9$ |
| $s_4$ | $3$ | $1$ | $0$ | $0$ | $0$ | $21$ | $21$ |
Para completar la tabla debemos hacer cero el resto de coeficientes de la columna de la variable que acaba de entrar $y$, así para la primera fila ($z$) debemos cambiar los valores sumando a los actuales los de la segunda fila multiplicados por cuatro para que en la columna de $y$ quede un cero, para la tercera fila ($s_2$) debemos restarle la segunda fila multiplicada por tres para que en la columna de $y$ quede también un cero, a la cuarta fila debemos restarle la segunda para que también quede un cero en la celda correspondiente de la columna de $y$, y finalmente a la quinta fila también debemos restarle la segunda para que quede un cero en la celda correspondiente de la columna de $y$:
Fila corresppondiente a $z$:
$\begin{matrix} -3 & -4 & 0 & 0 & 0 & 0 & 0\\ 0 & 4 & 4 & 0 & 0 & 0 & 24 \\ \hline -3 & 0 & 4 & 0 & 0 & 0 & 24 \end{matrix} $
Fila correspondiente a $s_2$:
$\begin{matrix} 1 & 3 & 0 & 1 & 0 & 0 & 19\\ 0 & -3 & -3 & 0 & 0 & 0 & -18 \\ \hline 1 & 0 & -3 & 0 & 0 & 0 & 1 \end{matrix} $
Fila correspondiente a $s_3$
$\begin{matrix} 1 & 1 & 0 & 0 & 1 & 0 & 9\\ 0 & -1 & -1 & 0 & 0 & 0 & -6 \\ \hline 1 & 0 & -1 & 0 & 1 & 0 & 3 \end{matrix} $
Fila correspondiente a $s_4$
$\begin{matrix} 3 & 1 & 0 & 0 & 0 & 0 & 21\\ 0 & -1 & -1 & 0 & 0 & 0 & -6 \\ \hline 3 & 0 & -1 & 0 & 0 & 0 & 15 \end{matrix} $
Con lo que la tabla queda de la siguiente manera:
| Entrada $\rightarrow$ | $x$ | $y$ | $s_1$ | $s_2$ | $s_3$ | $s_4$ | Paso 2 | $\downarrow$ |
| $z$ | $-3$ | $0$ | $4$ | $0$ | $0$ | $0$ | $z_2=24$ | Salida |
| $y$ | $0$ | $1$ | $1$ | $0$ | $0$ | $0$ | $6$ | |
| $s_2$ | $1$ | $0$ | $-3$ | $1$ | $0$ | $0$ | $1$ | $1 \div1=1$ |
| $s_3$ | $1$ | $0$ | $-1$ | $0$ | $1$ | $0$ | $3$ | $3 \div1=3$ |
| $s_4$ | $3$ | $0$ | $-1$ | $0$ | $0$ | $1$ | $15$ | $15 \div3=5$ |
El resto es iterar sobre lo mismo, repetimos los pasos:
Como vemos en la tabla anterior el coeficiente más negativo de $z$ corresponde a la variable $x$ por lo que ésta será la que se transforme en variable básica, mientras que el cociente de la última columna más pequeño corresponde a la variable $s_2$ por lo que será ésta la que salga. Entra por tanto la variable $x_1$ en el lugar de la variable $s_2$ y copiamos la fila correspondiente pero con todos los coeficientes divididos entre la celda confluencia de ambas que en este caso es la celda de color verde de la tabla anterior con un valor de $1$, por lo que no se ve alterada. Para obtener el resto de filas repetimos el proceso anterior, a la fila uno de $z$, sumamos la fila de $x$ multiplicada por 3, a la fila de $y$ no hay que hacele nada ya tiene un cero en la columna de $x$, a la fila de $s_3$ le restaremos la de $x$ para obtener el cero y finalmente a la fila de $s_4$ le restaremos la de $x$ multiplicada por tres:
Fila corresppondiente a $z$:
$\begin{matrix} -3 & 0 & 4 & 0 & 0 & 0 & 24\\ 3 & 0 & -9 & 3 & 0 & 0 & 3 \\ \hline 0 & 0 & -5 & 3 & 0 & 0 & 27 \end{matrix} $
Fila corresppondiente a $s_3$:
$\begin{matrix} 1 & 0 & -1 & 0 & 1 & 0 & 3\\ -1 & 0 & 3 & -1 & 0 & 0 & -1 \\ \hline 0 & 0 & 2 & -1 & 1 & 0 & 2 \end{matrix} $
Fila corresppondiente a $s_4$:
$\begin{matrix} 3 & 0 & -1 & 0 & 0 & 1 & 15\\ -3 & 0 & 9 & -3 & 0 & 0 & -3 \\ \hline 0 & 0 & 8 & -3 & 0 & 1 & 12 \end{matrix} $
| Entrada $\rightarrow$ | $x$ | $y$ | $s_1$ | $s_2$ | $s_3$ | $s_4$ | Paso 3 | $\downarrow$ |
| $z$ | $0$ | $0$ | $-5$ | $3$ | $0$ | $0$ | $z_3=27$ | Salida |
| $y$ | $0$ | $1$ | $1$ | $0$ | $0$ | $0$ | $6$ | $6 \div1=6$ |
| $x$ | $1$ | $0$ | $-3$ | $1$ | $0$ | $0$ | $1$ | $1 \div(-3)={\large{-\frac{1}{3}}}$ |
| $s_3$ | $0$ | $0$ | $2$ | $-1$ | $1$ | $0$ | $2$ | $2 \div2=1$ |
| $s_4$ | $0$ | $0$ | $8$ | $-3$ | $0$ | $1$ | $12$ | $12 \div8={\large{\frac{3}{2}}}$ |
Aun no hemos terminado el proceso debido a que queda todavía un coeficiente negativo en la fila de $z$, concretamente el de $s_1$, por tanto $s_1$ entra como variable básica, y sale $s_3$ cuyo cociente final es el más pequeño de entre los positivos. En la siguiente tabla comenzamos escribiendo en la primera columna $s_1$ en el lugar de $s_3$ y como fila la misma pero con todos los valores divididos entre $2$ que es la celda de confluencia de ambas variables. Una vez hecho esto modificamos la columna de $s_1$ para que todos los valores sean cero menos el mencionado verde que quedará en 1. En dicho proceso habrá que sumarle a la fina de $z$ cinco veces la fila de $s_1$ modificada, la la fila de $y$ restarle la fila de $s_1$ modificada, a la fila de $x$ sumarle la fila de $s_1$ modificada multiplicada por tres, y finalmente a la fila de $s_4$ restarle la fila de $s_1$ modificada multiplicada por ocho, estos cambios se recogen en las siguientes operaciones:
Fila corresppondiente a $z$:
$\begin{matrix} 0 & 0 & -5 & 3 & 0 & 0 & 27\\ 0 & 0 & 5 & {\large{-\frac{5}{2}}} & {\large{\frac{5}{2}}} & 0 & 5 \\ \hline 0 & 0 & 0 & {\large{\frac{1}{2}}} & {\large{\frac{5}{2}}} & 0 & 32 \end{matrix} $
Fila correspondiente a $y$:
$\begin{matrix} 0 & 1 & 1 & 0 & 0 & 0 & 6\\ 0 & 0 & -1 & {\large{\frac{1}{2}}} & {\large{-\frac{1}{2}}} & 0 & -1 \\ \hline 0 & 1 & 0 & {\large{\frac{1}{2}}} & {\large{-\frac{1}{2}}} & 0 & 5 \end{matrix} $
Fila correspondiente a $x$
$\begin{matrix} 1 & 0 & -3 & 1 & 0 & 0 & 1 \\ 0 & 0 & 3 & {\large{-\frac{3}{2}}} & {\large{\frac{3}{2}}} & 0 & 3 \\ \hline 1 & 0 & 0 & {\large{-\frac{1}{2}}} & {\large{\frac{3}{2}}} & 0 & 4 \end{matrix} $
Fila correspondiente a $s_4$
$\begin{matrix} 0 & 0 & 8 & -3 & 0 & 1 & 12 \\ 0 & 0 & -8 & 4 & -4 & 0 & -8 \\ \hline 0 & 0 & 0 & 1 & -4 & 1 & 4 \end{matrix} $
Y el resultado final de la tabla quedaría:
| $x$ | $y$ | $s_1$ | $s_2$ | $s_3$ | $s_4$ | Paso 4 | |
| $z$ | $0$ | $0$ | $0$ | ${\large{\frac{1}{2}}} $ | ${\large{\frac{5}{2}}} $ | $0$ | $z_4=32$ |
| $y$ | $0$ | $1$ | $0$ | ${\large{\frac{1}{2}}} $ | ${\large{-\frac{1}{2}}} $ | $0$ | $5$ |
| $x$ | $1$ | $0$ | $0$ | ${\large{-\frac{1}{2}}} $ | ${\large{\frac{3}{2}}} $ | $0$ | $4$ |
| $s_1$ | $0$ | $0$ | $1$ | ${\large{-\frac{1}{2}}} $ | ${\large{\frac{1}{2}}} $ | $0$ | $1$ |
| $s_4$ | $0$ | $0$ | $0$ | $1$ | $-4$ | $1$ | $4$ |
Ya no quedan valores negativos en la primera fila $z$ por lo que hemos terminado el proceso, con lo que como podemos ver en la tabla, el valor del mázimo no lo da el resultado de $z_4=32$ y los valores de las variables $x=4$ e $y=5$.
Ahora podemos resumir el proceso dando los valores de las variables y la función objetivo, y el recorrido a través de la gráfica del proceso:
Paso 1:
$(s_1,s_2,s_3,s_4)=(6,19,9,21)$; $(x,y)=(0,0)$; $z_1=0$
Paso 2:
$(s_1,s_2,s_3,s_4)=(0,1,3,15)$; $(x,y)=(0,6)$; $z_2=24$
Paso 3:
$(s_1,s_2,s_3,s_4)=(0,0,2,12)$; $(x,y)=(1,6)$; $z_3=27$
Paso 4: $\rightarrow \textbf{Máx}$
$(s_1,s_2,s_3,s_4)=(0,0,1,4)$; $(x,y)=(5,4)$; $z_4=32$
2. Esquema de la Programación Lineal
SÍNTESIS.
Programación Lineal.
La Programación Lineal es un enfoque matemático utilizado para maximizar o minimizar una función lineal, sujeta a un conjunto de restricciones lineales. Mostramos a continuación un resumen de los conceptos clave:
Objetivo: Maximizar o minimizar una función lineal llamada función objetivo. Esta función está compuesta por variables de decisión multiplicadas por coeficientes constantes.
Variables de Decisión: Son las incógnitas o variables que se buscan determinar para optimizar la función objetivo.
Función Objetivo: Es la expresión matemática que se busca maximizar o minimizar. Generalmente, se denota como $z=f(x,y)$ y está compuesta por la suma ponderada de las variables de decisión.
Restricciones Lineales: Son expresiones lineales que representan las limitaciones del problema. Pueden incluir igualdades o desigualdades.
Región Factible: Es el conjunto de soluciones que satisface todas las restricciones del problema. Es la intersección de las regiones definidas por cada restricción.
Punto Óptimo: Es el conjunto de valores de las variables de decisión que maximizan o minimizan la función objetivo dentro de la región factible.
Métodos de Resolución: Se utilizan algoritmos y técnicas específicas para encontrar la solución óptima. Algunos métodos comunes incluyen el método Gráfico, el método que proporciona la herramienta Solver (Excel) y el método Simplex.
Aplicaciones: La programación lineal se utiliza en una variedad de campos, como la economía, la logística, la ingeniería, la producción, la gestión de proyectos y la toma de decisiones empresariales.
En resumen, la programación lineal proporciona un marco matemático para optimizar procesos y recursos limitados, lo que la hace valiosa en la toma de decisiones y la planificación en diversos campos.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0