3. Métodos de resolución por ordenador
1. Herramientas digitales
Como hemos visto, los problemas de programación lineal pueden llegar a ser muy complicados, en realidad son así, porque en la vida real, los problemas no suelen depender sólo de dos variables sino que entran a jugar muchas más.
En estos casos, la complejidad del problema hace que sea necesario el uso de programas informáticos que nos resolverán el problema simplemente introduciendo los datos y dejando que sea el ordenador quién haga los cálculos.
En este apartado te presentamos dos, el método gráfico y el método solver, que estarán muy relacionados con nuestro reto, ya que nos permitirá resolver los problemas de transporte de una manera cómoda y sencilla y en los casos en los que necesitemos más de dos variables, el método solver nos dará la solución simplemente introduciendo los datos en el ordenador.
2. Conocemos el método gráfico
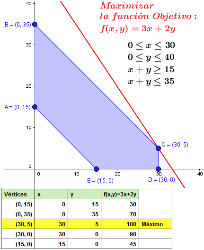
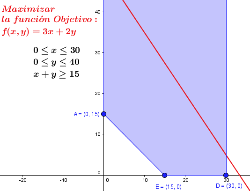
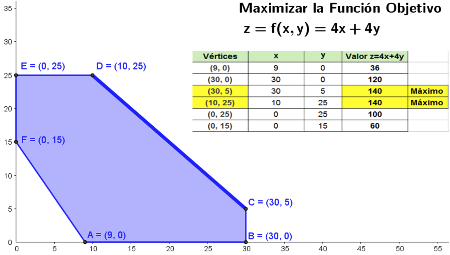
PLANTEAMIENTO GENERAL DEL PROBLEMA.
En un problema de programación lineal con dos variables, "x" e "y", se trata de hallar el óptimo (máximo o mínimo valor, según sea el caso) de la función: $f(x,y) = ax + by$, y los puntos en los que se alcanza, cuando "x" e "y" satisfacen el conjunto de condiciones:
$(I)\begin{Bmatrix}
a_1x & +b_2y & \leq c_1 \\
a_2x & +b_2y & \leq c_2 \\
...& ... & ... \\
a_mx & +b_my & \leq c_m\\
\end{Bmatrix}$
OBSERVACIONES:
1. La función lineal $f(x,y) = ax + by$ será la función objetivo del problema.
2. Las restricciones se componen del conjunto (I) de desigualdades lineales del tipo $(\geq),(\leq)$.
3. Las soluciones factibles serán el conjunto de pares (x, y) de números reales (o puntos del plano) que verifiquen todas las restricciones. Dicho conjunto forma un recinto convexo acotado, o bien, un recinto convexo no acotado.
4. Aquellas, de entre las soluciones factibles, que den el valor óptimo a la función objetivo, serán las soluciones óptimas del problema.
SITUACIONES QUE PUEDEN PRESENTARSE EN UN PROBLEMA DE PROGRAMACIÓN LINEAL.
Conviene señalar que no siempre existe solución óptima en este tipo de problemas, como se pone de manifiesto en los ejemplos que siguen, cuyo análisis gráfico muestra las situaciones que pueden presentarse.
1.- El conjunto de soluciones factibles es vacío. Por tanto, no existe solución óptima.
3.- El conjunto de soluciones factibles es un conjunto convexo no vacío y la función objetivo alcanza su valor máximo dentro de ese recinto en un vértice (Solución óptima).
2.- El conjunto de soluciones factibles es un conjunto convexo y no vacío; pero, no estando acotada en él la función objetivo, no existe solución óptima.
4.- El conjunto de soluciones factibles es un conjunto convexo no vacío y la función objetivo alcanza su máximo valor dentro de ese recinto en una arista del mismo. Por tanto, la solución óptima se alcanza en este caso, en todos los infinitos puntos de aquél segmento.
3. Uso de la herramienta Solver (Excel).
HERRAMIENTA SOLVER (EXCEL).
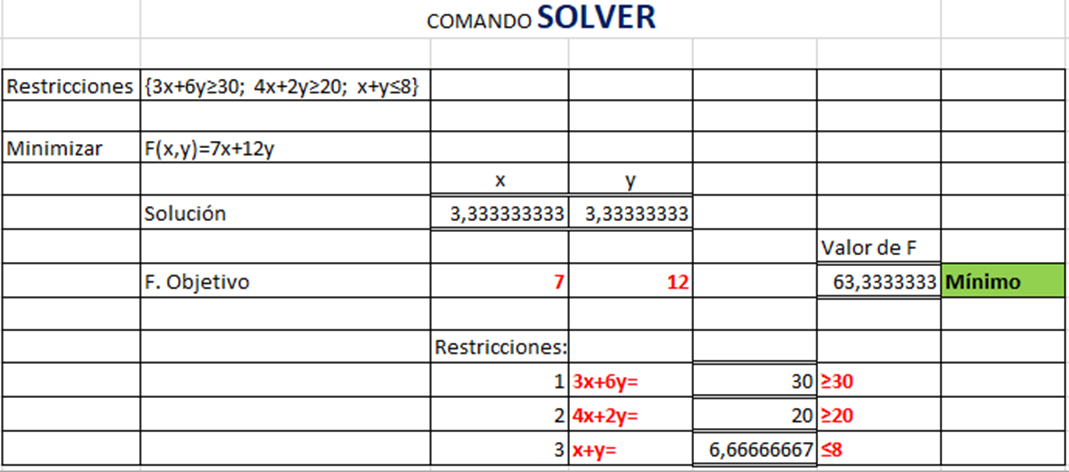
El procedimiento que seguimos ahora para encontrar la solución de forma analítica con la herramienta SOLVER es el mismo para cualesquiera que sea el número de variables. Vamos a explicarlo a través del siguiente Ejemplo:
Minimizar la función:
$F(x,y)=7x+12y$,
sujeta a las siguientes restricciones:
$\left . \begin{array}{l} 3x+6y\geq 30 \\ 4x+2y\geq20 \\ x+y\leq8 \\ x \geq 0 \\ y \geq 0 \end{array} \right \}$
Preparamos la Hoja de Cálculo (EXCEL) escribiendo en las celdas en modo texto el conjunto de Variables, Restricciones, Función Objetivo y si el Valor Óptimo es de Máximo o de Mínimo.
Como se ve en la tabla sólo usamos las celdas con doble barra para introducir valores numéricos y fórmulas según corresponda. Damos unos valores iniciales a x, y. Por ejemplo (1,1) y simplemente calculamos la celda que nos da el valor de la función objetivo y las correspondientes a las restricciones. En este caso, tenemos tres ya que la no negatividad la asume el propio recurso. Las demás casillas son meramente informativas. Nos vamos a la HC activando las pestañas:
DATOS$\rightarrow$ANÁLISIS DE DATOS$\rightarrow$ SOLVER
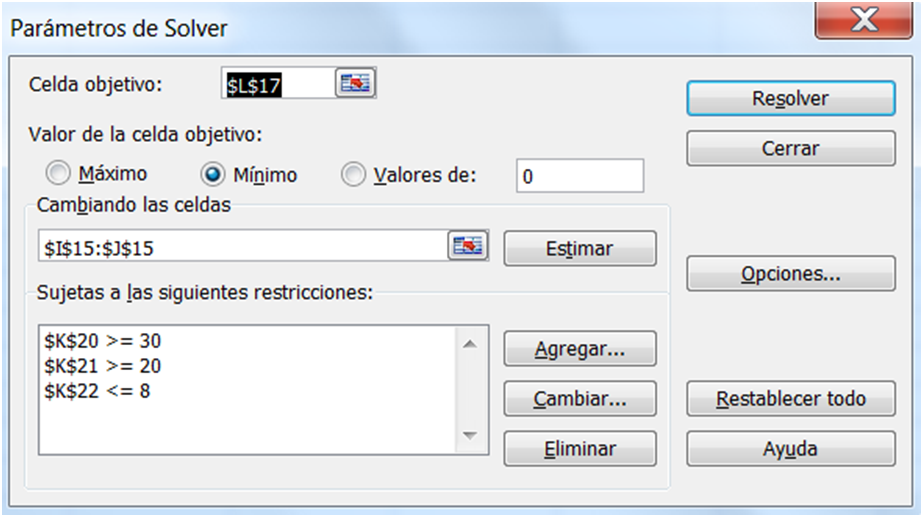
Al aparecer la siguiente ventana emergente, debemos completar los distintos campos que aparecen como son localización de las celdas de los valores de las variables y de la función objetivo, la clase de optimización (Máximo/ Mínimo) y las restricciones del problema:
Establecemos los parámetros en la ventana emergente de la
herramienta SOLVER.
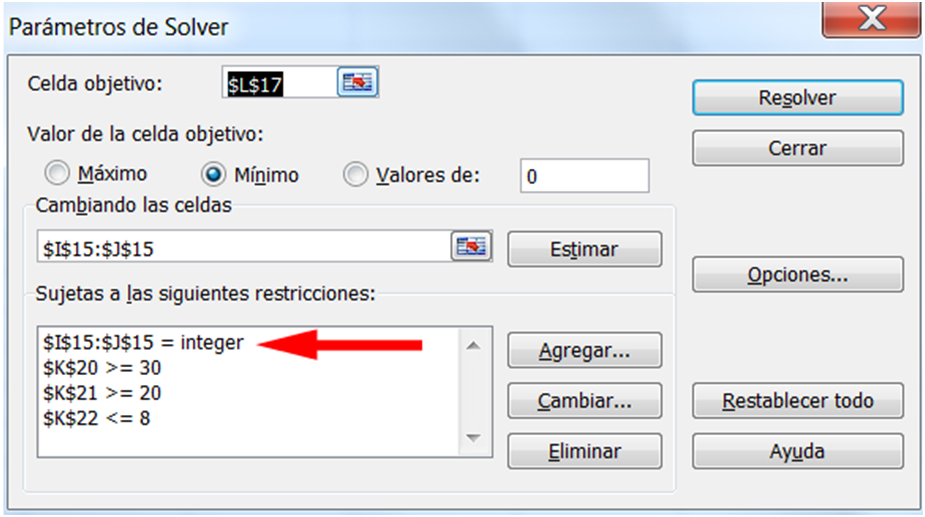
Si el problema es de variables enteras, debemos agregar esta
condición a las celdas de los valores
Seleccionamos la celda numérica asociada a la función objetivo. Elegimos la opción que corresponda {Máx/Mín} y a continuación agregamos el conjunto de restricciones usando tanto el comando Agregar como la localización de los valores donde están las restricciones y la desigualdad correspondiente. Si el problema es de variables enteras entonces debemos agregar esta condición a las celdas donde están situadas los valores de las variables. Finalmente indicamos la opción simplex LP y aceptamos. Como resultado de todo esto aparecerá en la HC la solución desarrollada.
Aquí tienes un video de como se lleva a cabo el proceso de introducción de datos en libre office:
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0