1. Grafo.

Un grafo se define como un conjunto de puntos, denominados nodos o vértices, que están interconectados por líneas conocidas como aristas. Se representa formalmente de la siguiente manera: $G=(Nodos, Aristas)$.

Los nodos o vértices representan los objetos del grafo, y las aristas representan las relaciones o conexiones entre estos objetos.

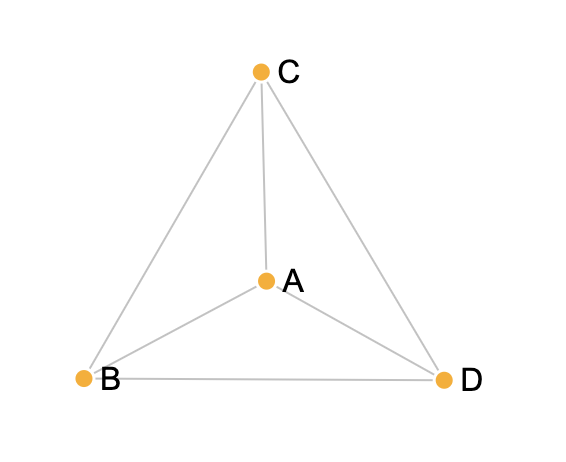
Ejemplo 1. Red de amistades

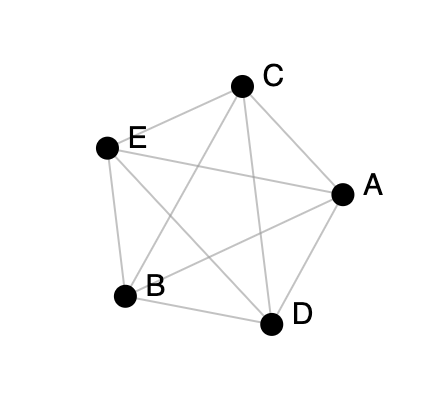
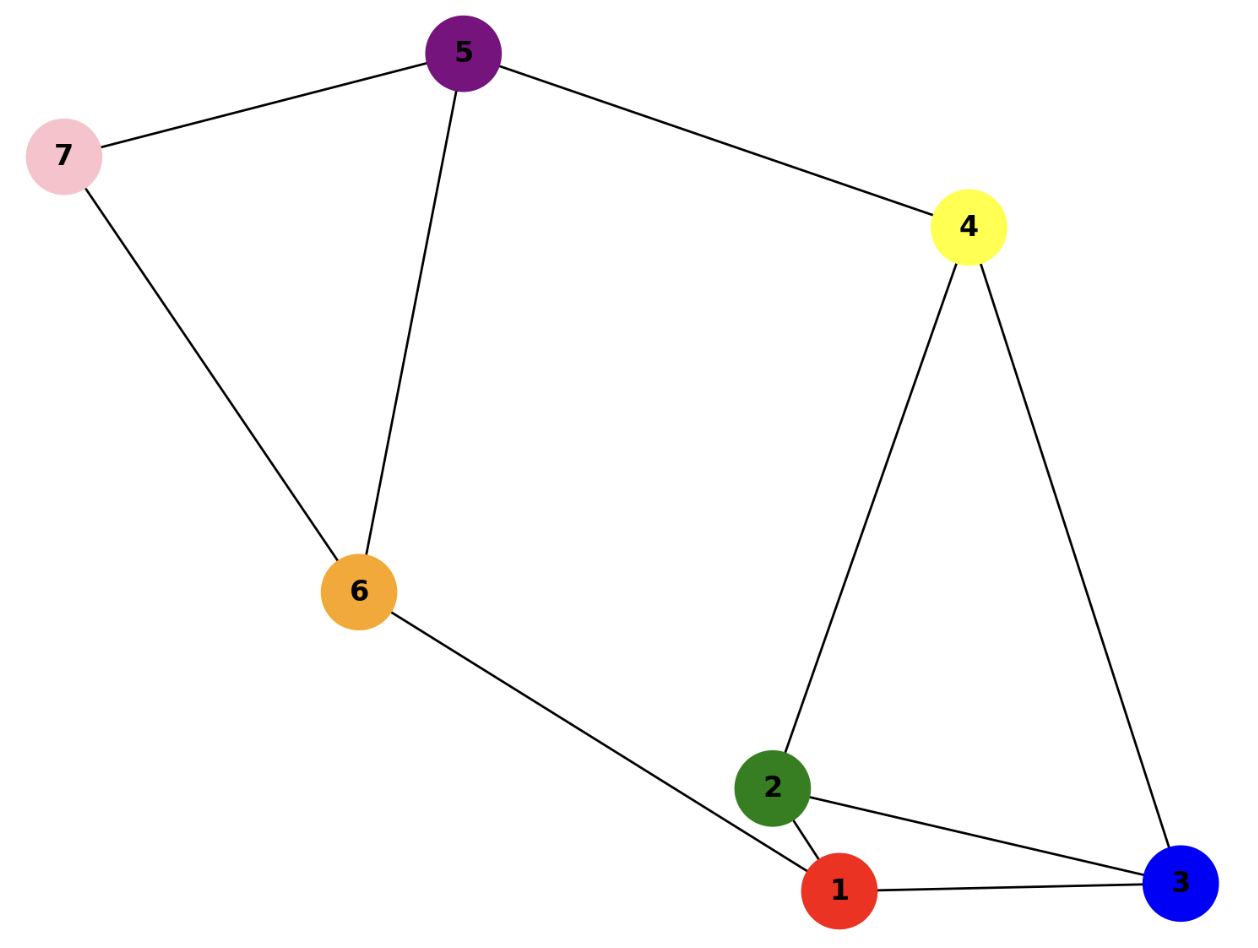
Los nodos representan las personas. Supongamos que $Nodos$ = {1, 2, 3 , 4, 5, 6}, donde Luis = 1, Álex = 2, Pedro = 3, Almudena = 4, Carmen = 5 y Natalia = 6.

Las aristas representan las amistades entre ellas. Supongamos que $Aristas$ = {{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {2, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}}, donde {1, 2} significa que 1 es amigo de 2 (Luis de Álex), {2, 4} indica que Álex es amigo de Almudena, etc.

En este ejemplo, el grafo modela una red de amistades donde cada persona es un vértice, y una arista entre dos personas indica que son amigas. Este sería un grafo no dirigido, ya que la amistad se considera mutua.

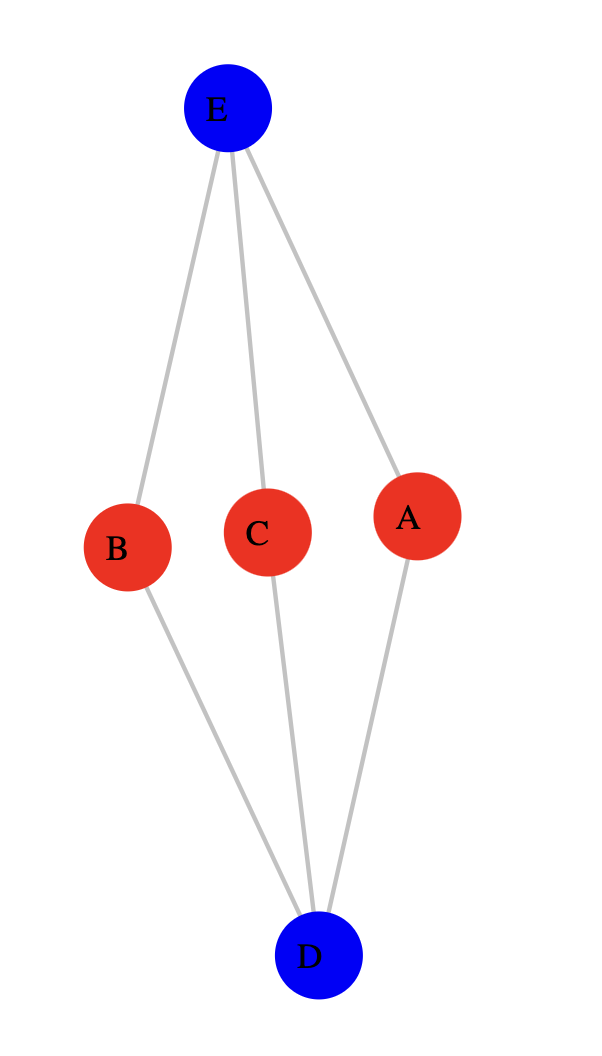
En la siguiente imagen se muestra una representación del grafo en forma de diagrama.

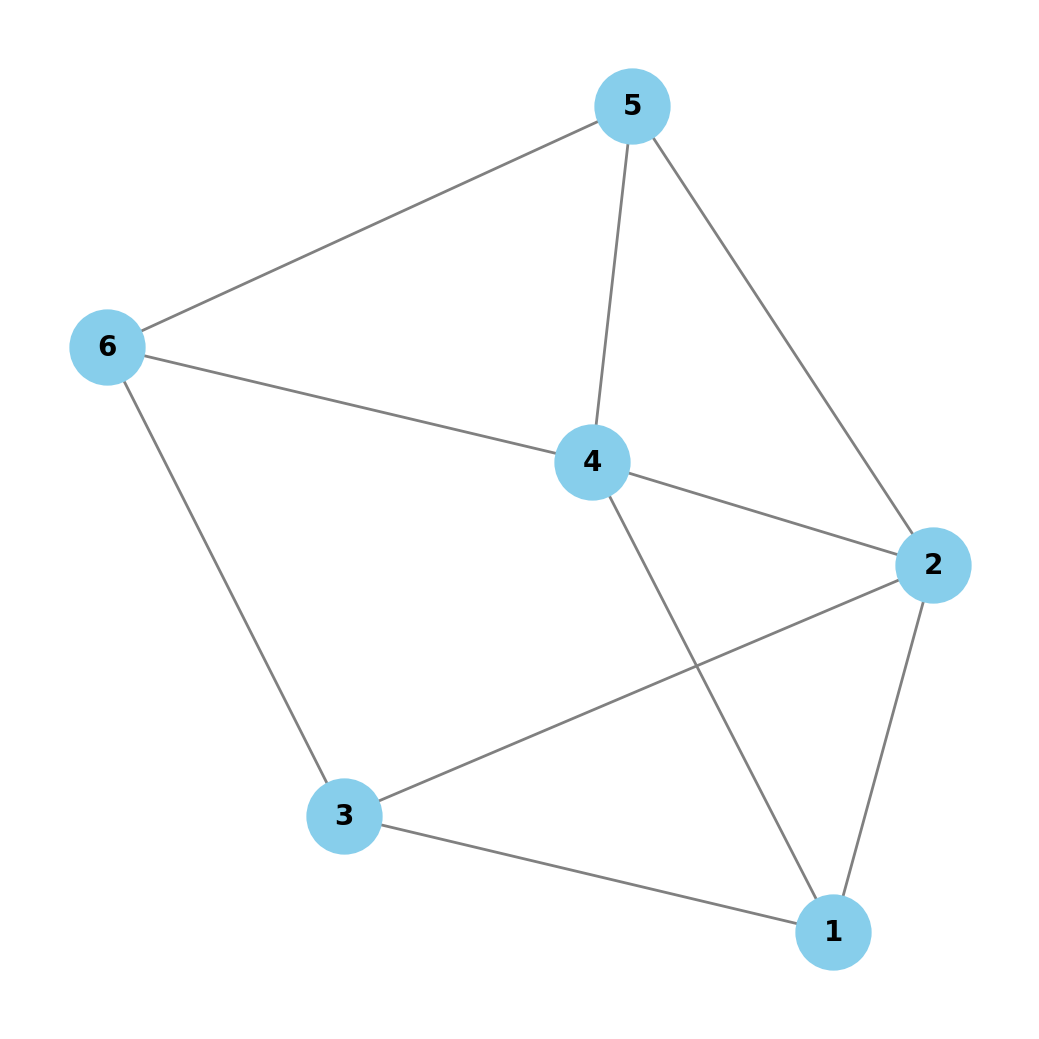
Representar grafos mediante un diagrama de puntos y líneas es útil porque proporcionan una representación visual inmediata de la estructura del grafo, lo que ayuda a comprender rápidamente las relaciones entre los elementos.

2. Subgrafo

Un subgrafo es una parte constituyente de un grafo, definido por un subconjunto de los vértices del grafo original y un subconjunto de las aristas que conectan esos vértices.

Formalmente, si tenemos un grafo \(G = (V, A)\) donde \(V\) es el conjunto de vértices y \(A\) es el conjunto de aristas, entonces un subgrafo \(G' = (V', A')\) cumple las condiciones de que \(V' \subseteq V\) y \(A' \subseteq A\), con cada arista en \(A'\) conectando solo vértices que están en \(V'\).

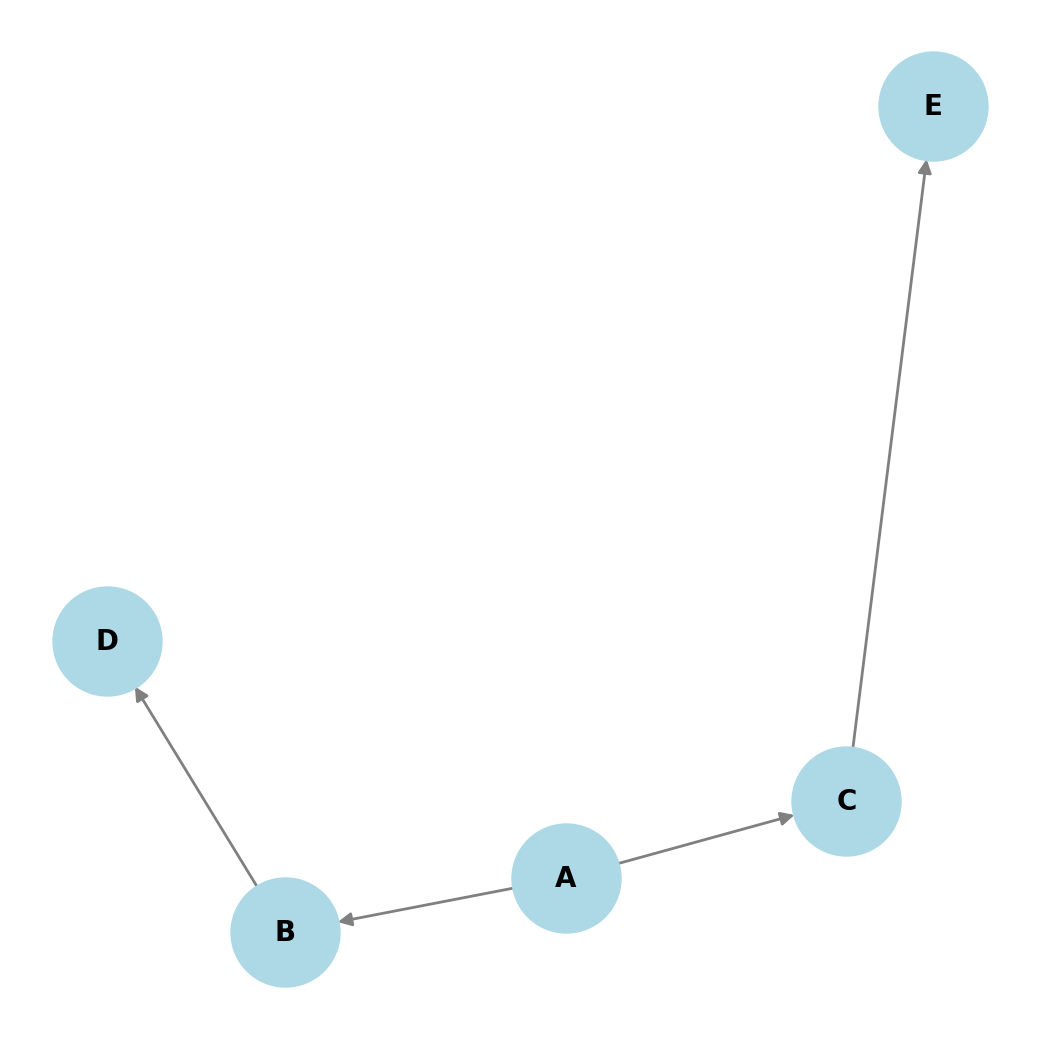
La siguiente imagen muestra un subgrafo, representado mediante un diagrama, del grafo anterior.  \(G' = (V', A')\) representa las llamadas telefónicas que los amigos realizaron ayer.

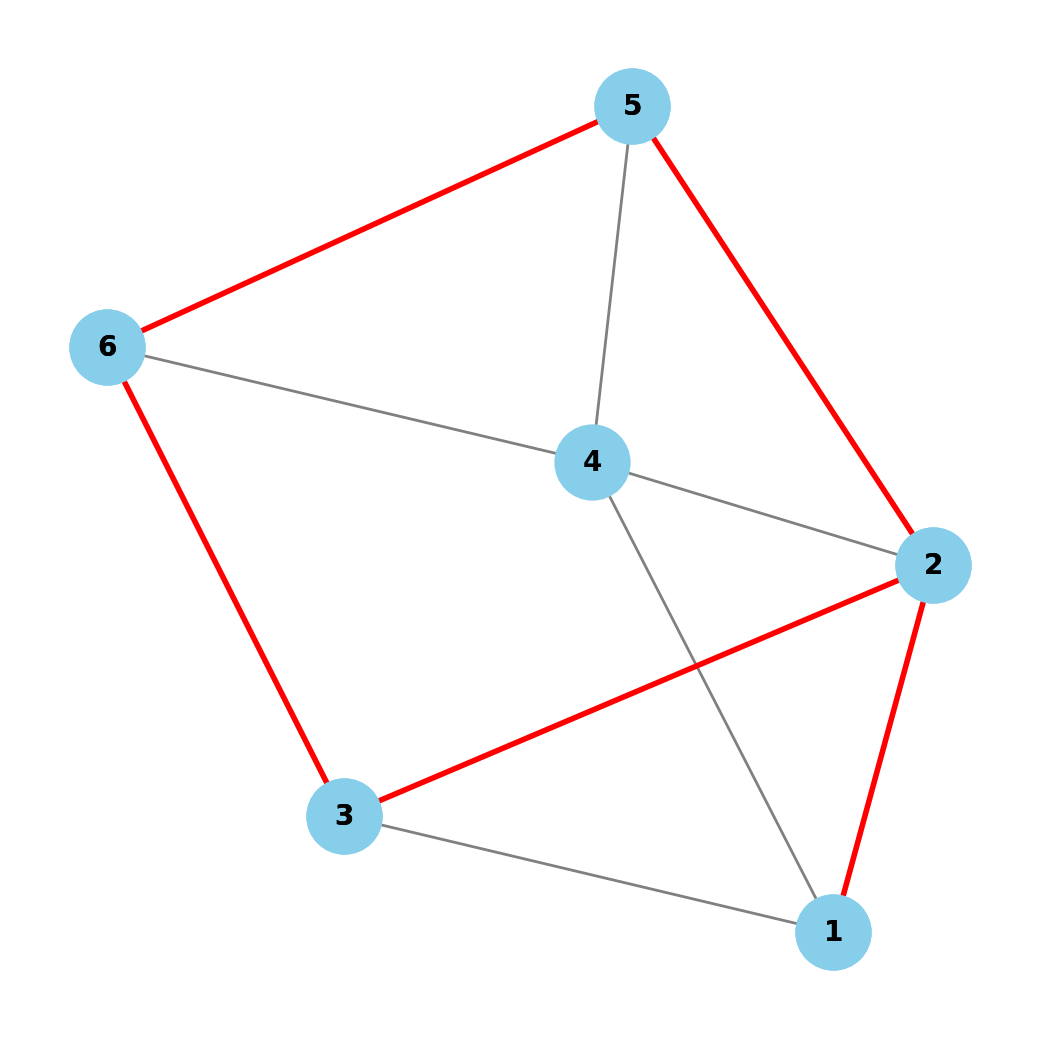
En el diagrama, se puede verificar fácilmente que:

- 1 (Luis) habló con 2 (Álex)

- 2 (Álex) habló con 1 (Luis), con 3 (Pedro) y con 5 (Carmen), etc.

3. Comunidades

Un caso particular de subgrafos son las comunidades. Una comunidad se refiere a un grupo de vértices que están más densamente conectados entre sí que con el resto de vértices del grafo. Estas comunidades, debido a su mayor densidad de conexiones internas, forman subestructuras dentro del grafo principal que cumplen con la definición de subgrafo.

Ejemplo 2. Red social

Imagina una red social pequeña donde los miembros interactúan principalmente dentro de sus círculos cercanos, pero también hay algunas conexiones entre personas de diferentes círculos. En este contexto, el grafo interactivo (puedes mover los nodos) que se muestra a continuación representa la red de amistades entre un grupo de personas, identificadas por las letras A, B, C, D, E, F, G, H, e I. Las comunidades dentro de este grafo pueden interpretarse como grupos de amigos que interactúan más frecuentemente entre sí.

Aquí está la descripción de las comunidades y sus relaciones:

1. Comunidad 1 (Grupo de amigos 1):
   • Miembros: A, B, C
   • Descripción: este grupo consiste en tres amigos cercanos que comparten intereses comunes como deportes y música. A, B, y C se conocen desde hace mucho tiempo y tienen una sólida relación de amistad. Se reúnen a menudo para practicar deportes y asistir a conciertos juntos.
2. Comunidad 2 (Grupo de amigos 2):
   • Miembros: D, E, F
   • Descripción: D, E, y F son colegas que trabajan en la misma empresa y han formado una fuerte amistad. Regularmente almuerzan juntos y colaboran en varios proyectos. Además, comparten un interés en la tecnología y a menudo debaten sobre las últimas tendencias en su campo.
3. Comunidad 3 (Grupo de amigos 3):
   • Miembros: G, H, I
   • Descripción: este grupo está formado por estudiantes universitarios que se conocieron en un club de arte y literatura. G, H, e I disfrutan organizando eventos de poesía y asisten juntos a exposiciones de arte. Tienen una relación estrecha basada en su pasión compartida por las artes.

Conexiones entre comunidades:

• A y D: A conoció a D en un evento de networking y desde entonces han mantenido contacto, compartiendo ideas y consejos sobre sus respectivos campos de interés.
• E e I: E e I se conocieron a través de un proyecto comunitario y descubrieron que tienen amigos en común. Aunque pertenecen a diferentes círculos, ocasionalmente se reúnen en eventos sociales y mantienen una relación amistosa.

En esta red social, las personas tienden a interactuar más dentro de sus propios grupos, pero las conexiones entre diferentes comunidades muestran que también hay intercambio y comunicación entre distintos círculos de amigos. Esta estructura de red permite la formación de relaciones diversas y la difusión de información e intereses entre diferentes grupos.

Observa que se conserva la estructura de las comunidades aunque arrastremos cualquiera de los nodos.

Dos grafos son esencialmente iguales (isomorfos) si tienen la misma estructura subyacente.  Esto significa que existe una correspondencia uno a uno entre los vértices del primer grafo y los vértices del segundo grafo de tal manera que las conexiones (aristas) entre los vértices se preservan.

Dos grafos isomorfos pueden parecer diferentes a primera vista debido a la disposición de sus vértices y aristas.

Observa la siguiente escena interactiva:

Arrastra los vértices en la escena anterior hasta conseguir una disposición de vértices como la que se muestra a continuación:

Como puedes comprobar, ambos grafos son esencialmente iguales, aunque en el primero, las aristas se cruzan, mientras que en el segundo, no lo hacen.

El concepto de isomorfismo es importante porque muestra que las propiedades estructurales de los grafos no dependen de la manera en que se dibujan, sino de cómo están conectados sus elementos. En otras palabras, dos grafos isomorfos son "esencialmente" el mismo grafo, solo que representado o etiquetado de manera diferente. Cabe destacar que, en el ejemplo previo mencionado, las etiquetas también coinciden.

Los grafos son estructuras de datos compuestas por nodos (también llamados vértices) conectados por aristas (o enlaces). La naturaleza de las conexiones entre los nodos determina si un grafo es dirigido o no dirigido.

Grafos no dirigidos
En un grafo no dirigido, las aristas entre los nodos son bidireccionales, lo que significa que si hay una conexión entre el nodo A y el nodo B, puedes ir de A a B y de B a A sin distinción. Estas conexiones no tienen una dirección específica. Los grafos no dirigidos se utilizan para representar relaciones simétricas, como la amistad en una red social, donde si A es amigo de B, entonces B también es amigo de A.

Grafos dirigidos (Digrafos)
Un grafo dirigido, o digrafo, tiene aristas dirigidas que conectan los nodos. Cada arista tiene una dirección, señalada de un nodo de origen a un nodo de destino. Estas se pueden y suelen dibujar como flechas para indicar la dirección de la relación entre dos nodos, lo que ayuda a visualizar claramente la dirección de la relación o conexión en el grafo.

Esto significa que si existe una arista dirigida del nodo A al nodo B, no necesariamente hay una arista del nodo B al nodo A, a menos que se especifique explícitamente. Los grafos dirigidos se usan para representar relaciones asimétricas, como la web, donde una página A puede tener un enlace a una página B sin que B enlace a A.

Grafo completo

Un grafo completo es un tipo de grafo en el que cada par de nodos distintos está conectado por una arista. En otras palabras, todos los nodos están directamente conectados entre sí sin excepciones. La característica principal de un grafo completo es que es densamente conectado.

Para un grafo no dirigido, el número de aristas \(A\) en un grafo completo con \(N\) nodos se calcula mediante la fórmula: $ A = {\large{\frac{N(N - 1)}{2}}} $.

A continuación se presentan las representaciones de un grafo $K_4$ y de un grafo $K_5$.

Los grafos completos tienen aplicaciones en el estudio de redes donde cada nodo necesita estar conectado con todos los demás, como en el caso de problemas de diseño de redes de telecomunicaciones, donde se desea que cada sitio esté directamente conectado a todos los demás para minimizar el tiempo de tránsito de la información.

Grafo bipartito

Un grafo bipartito es un tipo de grafo donde los vértices (nodos) se pueden dividir en dos conjuntos disjuntos (que no tienen nodos comunes) $U$ y $V$ tales que cada arista conecta un vértice en $U$ con uno en $V$. No existen aristas que conecten vértices dentro del mismo conjunto. Esto significa que es posible colorear los vértices de un grafo bipartito con solo dos colores, de tal manera que no hay dos vértices adyacentes (conectados) del mismo color.

Ejemplo.

Imagina que eres el jefe de estudios de un centro educativo y debes planificar el horario de clases para el próximo trimestre. El centro dispone de tres aulas (Aula 1, Aula 2, Aula 3) y ofrece cuatro cursos diferentes (Matemáticas, Historia, Ciencias, Literatura). Debido a las restricciones de espacio y tiempo, no todos los cursos se pueden impartir en todas las aulas. Además, algunos cursos tienen requisitos específicos de equipamiento que solo ciertas aulas cumplen. El desafío es asignar cada curso a una aula adecuada, asegurando que todos los cursos se impartan y que las necesidades de cada uno sean satisfechas.

La información específica de las posibles asignaciones es la siguiente:

• Aula 1 está equipada con laboratorio de ciencias, por lo que es adecuada para el curso de Ciencias.
• Aula 2 es la más grande y puede acomodar cualquier curso, pero se prefiere para Matemáticas y Literatura debido a su sistema de proyección y espacio para discusiones en grupo.
• Aula 3 tiene una configuración más tradicional, ideal para Historia y Literatura.

Además,

• El curso de Matemáticas requiere pizarras adicionales, por lo que solo se puede impartir en el Aula 2.
• Ciencias solo se puede impartir en el Aula 1 debido a la necesidad del laboratorio.
• Historia y Literatura pueden impartirse en cualquier aula, pero hay una preferencia por las Aulas 2 y 3, debido a la configuración y recursos disponibles.

El objetivo es crear un horario que utilice eficientemente las aulas disponibles y cumpla con los requisitos específicos de cada curso. Se debe formar un grafo bipartito donde un conjunto de vértices represente los cursos y el otro conjunto represente las aulas. Las aristas entre los cursos y las aulas indicarán las asignaciones posibles según las restricciones dadas.

Este grafo bipartito ayuda a visualizar claramente cómo se pueden asignar los recursos (aulas) a las tareas (cursos) de manera efectiva.

Grafo bipartito completo

Un grafo bipartito completo es un caso especial de grafo bipartito en el que cada vértice de un conjunto está conectado a todos los vértices del otro conjunto. En otras palabras, si dividimos el grafo en dos conjuntos \(U\) y \(V\), cada vértice en \(U\) tiene una arista hacia cada vértice en \(V\), y viceversa. Este tipo de grafo se denota como \(K_{m,n}\), donde \(m\) y \(n\) son las cantidades de vértices en los conjuntos \(U\) y \(V\), respectivamente.

A continuación se presentan las representaciones de un grafo \(K_{3,2}\) y de un grafo \(K_{3,3}\).

Este tipo de grafos se utiliza en situaciones donde es importante asegurar que todos los elementos de un conjunto estén relacionados de alguna manera con todos los elementos del otro conjunto. Por ejemplo:

- Asignación de tareas: Si tienes un conjunto de trabajadores y un conjunto de tareas, y cada trabajador puede realizar cualquier tarea, un grafo bipartito completo puede representar todas las posibles asignaciones de trabajadores a tareas.
- Modelado de relaciones: En las redes sociales, modelos bipartitos completos pueden ser utilizados para representar, por ejemplo, la relación entre usuarios y grupos o eventos, donde todos los usuarios están interesados o relacionados con todos los eventos.

Un grafo plano es un tipo de grafo que se puede dibujar en el plano sin que ninguna de sus aristas se crucen entre sí. En otras palabras, se puede representar en una superficie plana de tal manera que sus vértices sean puntos y sus aristas sean líneas curvas o rectas que conectan estos puntos, sin que ninguna arista cruce a otra excepto en los vértices donde se unen.

Algunos grafos pueden parecer no ser planos a primera vista, pero en realidad sí lo son. Este es el caso de \(K_{3,2}\). Al reposicionar sus vértices adecuadamente, se demuestra que este grafo es, de hecho, plano.

Los grafos planos son especialmente relevantes en campos como la geometría computacional, el diseño de circuitos y las redes.

Estas son algunas de sus aplicaciones:

• Diseño de circuitos integrados: en la planificación de la disposición de los circuitos en un chip, donde se busca evitar el cruce de conexiones. 
• Planificación urbana y de redes: en la disposición de carreteras, servicios públicos y redes de comunicaciones, buscando eficiencia y minimización de interferencias. Es esencial evitar cruces innecesarios que pueden llevar a congestiones o a la necesidad de construir infraestructura compleja como puentes o túneles.