1. Los grafos en nuestra vida diaria
¿Alguna vez has jugado a conectar puntos en un papel para dibujar una figura? O quizás, ¿has pensado en la mejor ruta para ir de un lugar a otro en tu ciudad? Si es así, ya has comenzado a pensar en términos de grafos sin siquiera darte cuenta.
¿Qué es un Grafo?
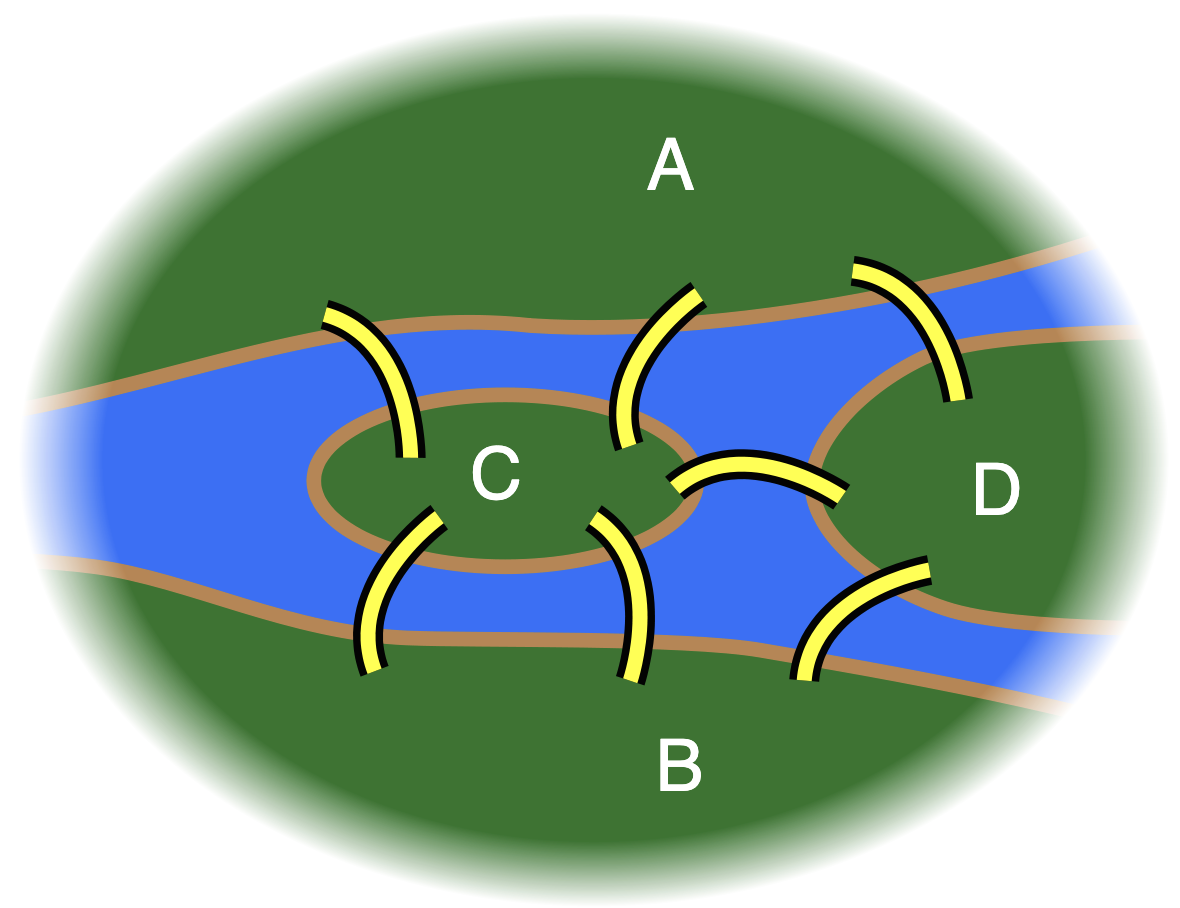
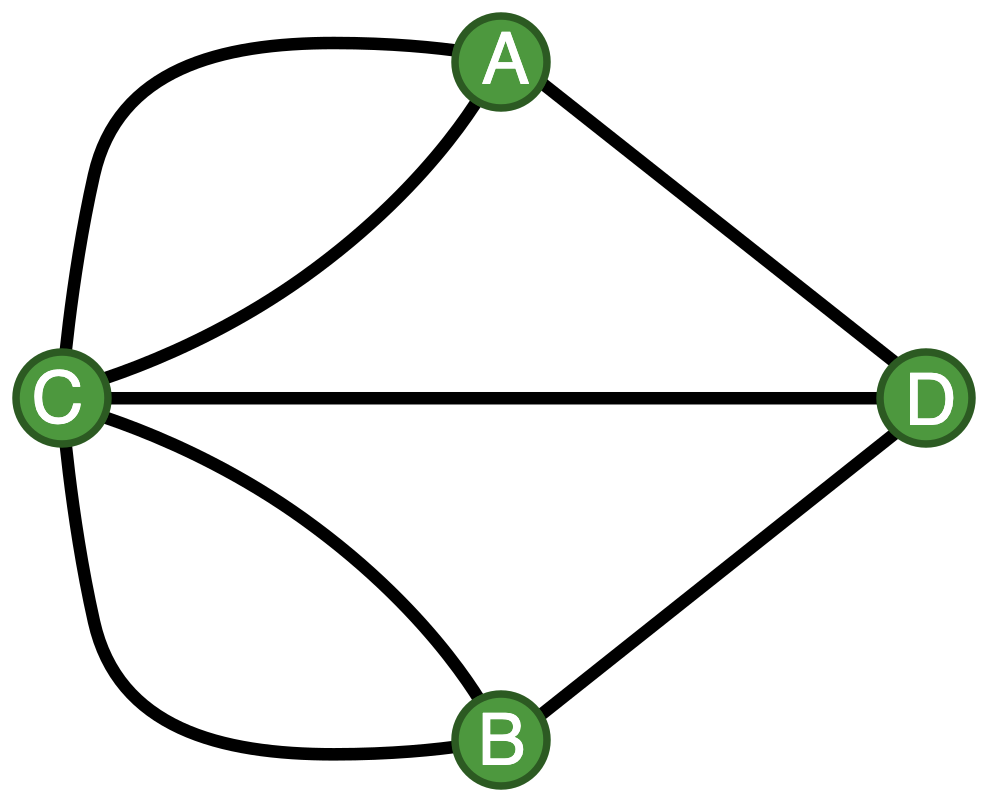
Un grafo es una forma de representar relaciones entre pares de objetos. Estos objetos son llamados nodos (o vértices), y las relaciones entre ellos se representan mediante líneas llamadas aristas. Si imaginamos los nodos como puntos en un mapa, las aristas serían las carreteras o caminos que los conectan.
La belleza de los grafos radica en su versatilidad. Aquí hay algunos ejemplos de cómo se utilizan en la vida real:
Redes Sociales: en plataformas como Facebook o Twitter, cada usuario puede ser visto como un nodo, y las amistades o seguidores serían las aristas que los conectan. Analizar estos grafos ayuda a entender cómo se difunde la información o cómo se forman las comunidades en línea.

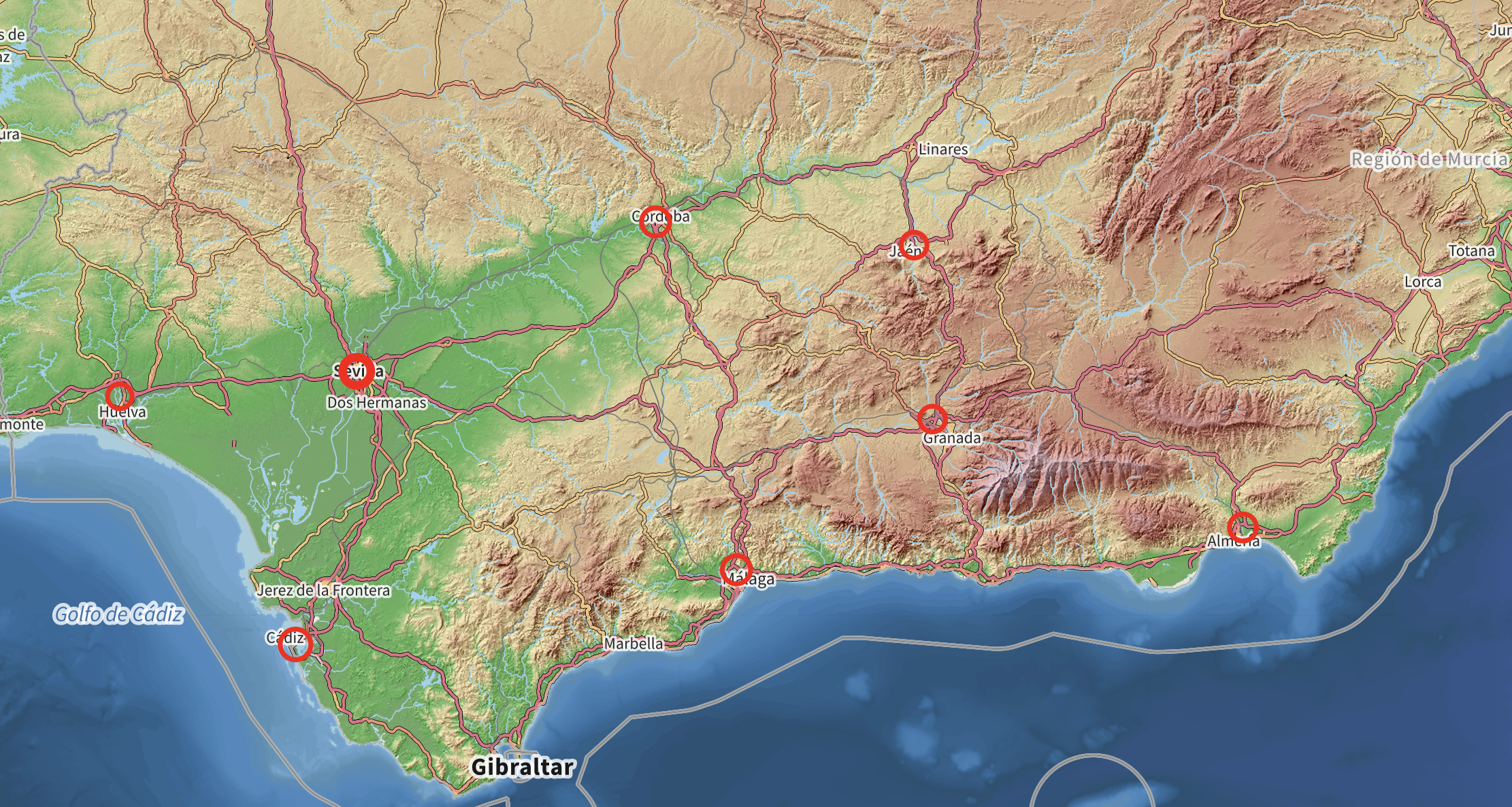
Sistemas de Navegación: cuando usamos una aplicación para encontrar la ruta más corta entre dos puntos, estamos utilizando algoritmos basados en la teoría de grafos. Los lugares son nodos y las carreteras son aristas, y el algoritmo busca el camino que minimiza tiempo o distancia.

Internet: toda la estructura de Internet puede considerarse como un enorme grafo, donde los sitios web son nodos y los enlaces entre ellos son aristas. Comprender este grafo es crucial para mejorar la eficiencia de la red y la velocidad de navegación.

¿Por qué estudiar grafos?
Además de ser increíblemente útiles para resolver problemas reales, los grafos nos ayudan a desarrollar habilidades de pensamiento crítico y analítico. Nos permiten visualizar y modelar complejidades de manera simplificada, ofreciéndonos una poderosa herramienta para entender y mejorar el mundo que nos rodea.
A medida que avancemos, exploraremos cómo construir y analizar grafos, aprenderemos sobre algoritmos específicos para resolver distintos tipos de problemas y veremos cómo esta teoría se aplica en campos muy diversos.