Como vimos en el apartado 2. El lenguaje de las funciones, la tasa de variación media de una función \( f(x) \) en el intervalo \([a, a+h]\) se define como el cociente de la variación en \( f(x) \) por la variación en \( x \) sobre ese intervalo. Matemáticamente, esto se expresa como: 

$ \text{Tasa de variación media en [a,a+h]} = {\large{\frac{f(a+h) - f(a)}{h} }}$

Recuerda que dicho cociente es la pendiente de la línea recta que conecta los puntos $(a,f(a))$ y $(a+h,f(a+h))$ en el gráfico de la función \( f(x) \).

La derivada de una función \( f(x) \) en un punto "a" se define a partir del concepto de la tasa de variación media de la función en un intervalo \([a, a+h]\). Esto se debe a que la derivada es, conceptualmente, la tasa de variación instantánea de la función en un punto específico, lo cual se logra reduciendo el intervalo hasta que es infinitesimal, es decir, tomando el límite de esta tasa de variación media a medida que \( h \) se acerca a 0.

Por lo tanto, la derivada de \( f(x) \) en el punto \( a \), denotada como \( f'(a) \) o ${\large{\frac{df}{dx}|_{x=a}}}$, se define como el límite:

$ f'(a) =\underset{h \to 0}{lim} {\large{\frac{f(a+h) - f(a)}{h}}} $

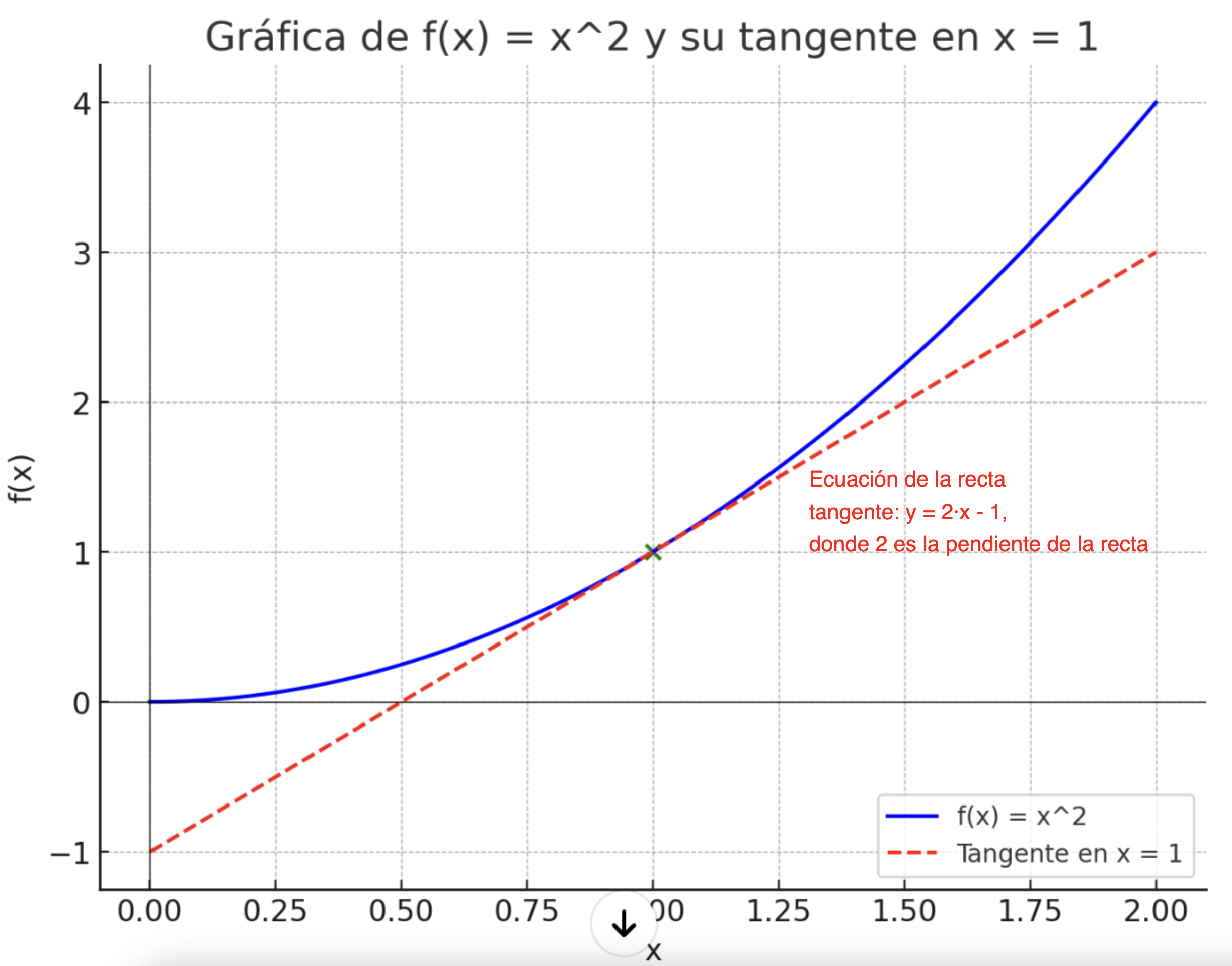
Esta definición recoge la idea de que la derivada en un punto es la pendiente de la recta tangente a la gráfica de la función en ese punto, representando así la tasa de variación instantánea de la función en \( a \).

En la escena de Geogebra que se muestra a continuación, \( \text{TVM[a,a+h]} = {\large{\frac{f(a+h) - f(a)}{h}}} \) representa la pendiente de la recta (color azul) que une los puntos A y B. Al desplazar el deslizador $h$ hacia la izquierda, puedes observar como el punto $B$ se acerca al punto $A$ a través de la gráfica de la función. Cuando $h$ alcanza el valor 0, la cuerda se convierte en la recta tangente (color verde) a la función en el punto $a$, siendo la pendiente de dicha recta tangente, la derivada de \( f(x) \) en el punto \( a \) denotada como $ f'(a) =\underset{h \to 0}{lim} {\large{\frac{f(a+h) - f(a)}{h}}} $

La función derivada de \( f(x) \), denotada como \( f'(x) \) o \( {\large{\frac{df}{dx}}} \), es una función que nos da la pendiente de la recta tangente a la gráfica de \( f(x) \) en cada punto. Matemáticamente, la derivada en un punto mide la tasa de variación instantánea de \( f(x) \) con respecto a \( x \). En términos más simples, nos dice cuánto cambia \( f(x) \) cuando \( x \) varía un poco.

 La derivada de \( f(x) \) en un punto \( x \) se define como:
   \[
   f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
   \]

En el siguiente vídeo encontrarás una explicación que te ayudará a comprender la utilidad de la función derivada.