Límite de una función en un punto

El límite de una función cuando la variable \( x \) tiende a un número \( a \) se refiere a lo que sucede con los valores de esa función a medida que \( x \) se aproxima cada vez más a \( a \). No se trata del valor de la función en \( a \) mismo, sino del valor al que se aproxima la función cuando \( x \) está muy cerca de \( a \). 

Se pueden dar dos situaciones: que el resultado del límite sea un número o que sea infinito (ya sea $+\infty$  o   $-\infty$)

Caso 1

Por ejemplo, consideremos la función $ f(x) = {\large{\frac{(x^2 - 1)}{(x - 1)}}}$

Al calcular \( f(1) \), nos encontramos con una división entre 0, lo que es indefinido. Sin embargo, si observamos el comportamiento de \( f(x) \) a medida que \( x \) se acerca a 1 (por ejemplo, 0.9, 0.99, 0.999, etc.), los valores de \( f(x) \) se acercan a 2. De igual manera ocurre si nos aproximamos al valor 1 de x  por la derecha, dando valores cada vez más próximos a uno (por ejemplo, 1.1, 1.01, 1.001, etc) en este caso los valores de \( f(x) \) también se acercan a 2. Esto es lo que se denomina límites laterales y se expresan igual que el límite cuando x tiende a uno, pero poniendo una especie de exponente a ese uno, con un "+" si nos acercamos por la derecha o un "-" si lo hacemos por la izquierda:

Cuando esto ocurre, y los dos límites laterales valen lo mismo podemos decir que existe el límite de la función cuando x tiende a ese valor y vale ese resultado, en este caso:

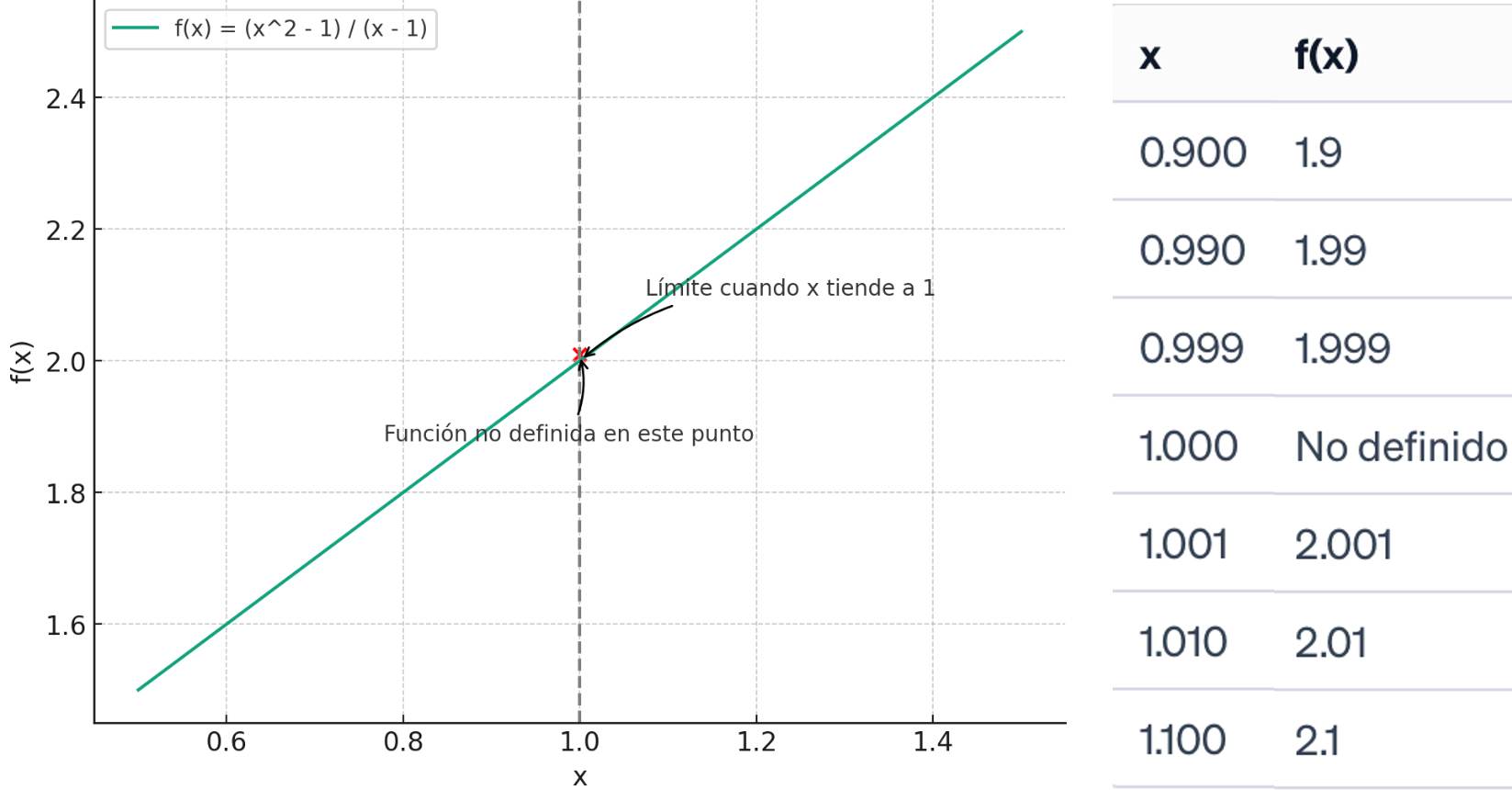
$\underset {x \to 1}{lim} \left( {\large{\frac{x^{2}-1}{x-1 }}} \right)=2$ 

Esto nos dice que, aunque \( f(x) \) no está definida en \( x = 1 \), a medida que \( x \) se acerca a 1, los valores de \( f(x) \) se acercan a 2.

La siguiente imagen muestra la gráfica de la función y su comportamiento en las proximidades de 1.

En el siguiente vídeo se explica el concepto de límite de una función en un punto.

Caso 2

Por ejemplo, consideremos la función  $f(x) = {\large{\frac{1}{x}}}$.

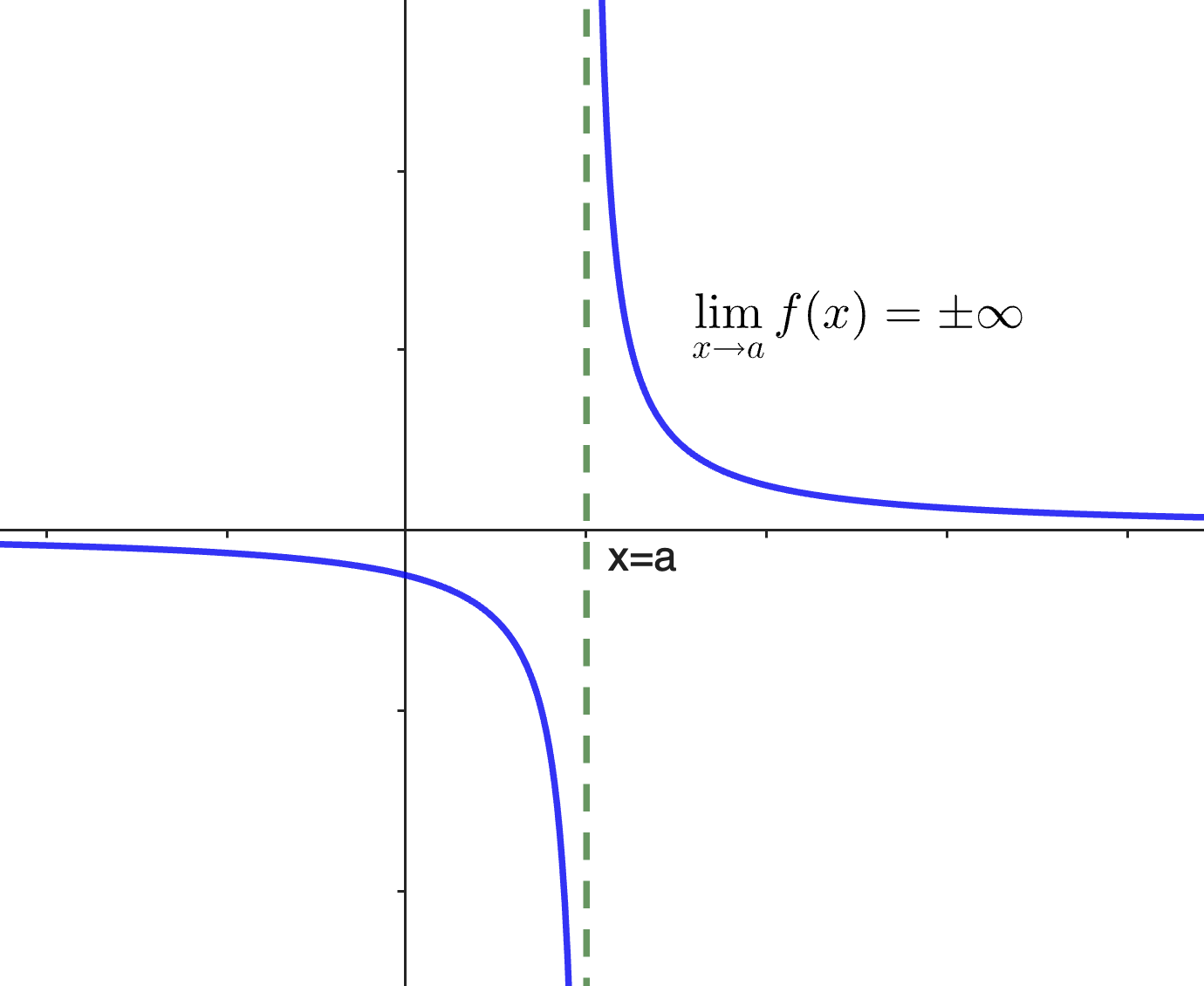
 A medida que \( x \) se acerca a 0 desde el lado positivo, \( f(x) \) se hace más y más grande positivamente, es decir, tiende a \( +\infty \). Desde el lado negativo, \( f(x) \) se hace más y más grande negativamente, es decir, tiende a \( -\infty \). Aquí, \( x = 0 \) es una asíntota vertical. Si estudiamos los límites laterales obtenemos:

Cuando esto ocurre y los dos límites laterales no valen lo mismo, podemos decir que no existe el límite de la función cuando x tiende a ese valor, aunque si existen los límites laterales:

$\underset {x \to 0}{lim} \left( {\large{\frac{1}{x }}} \right)=\text{No Existe}$

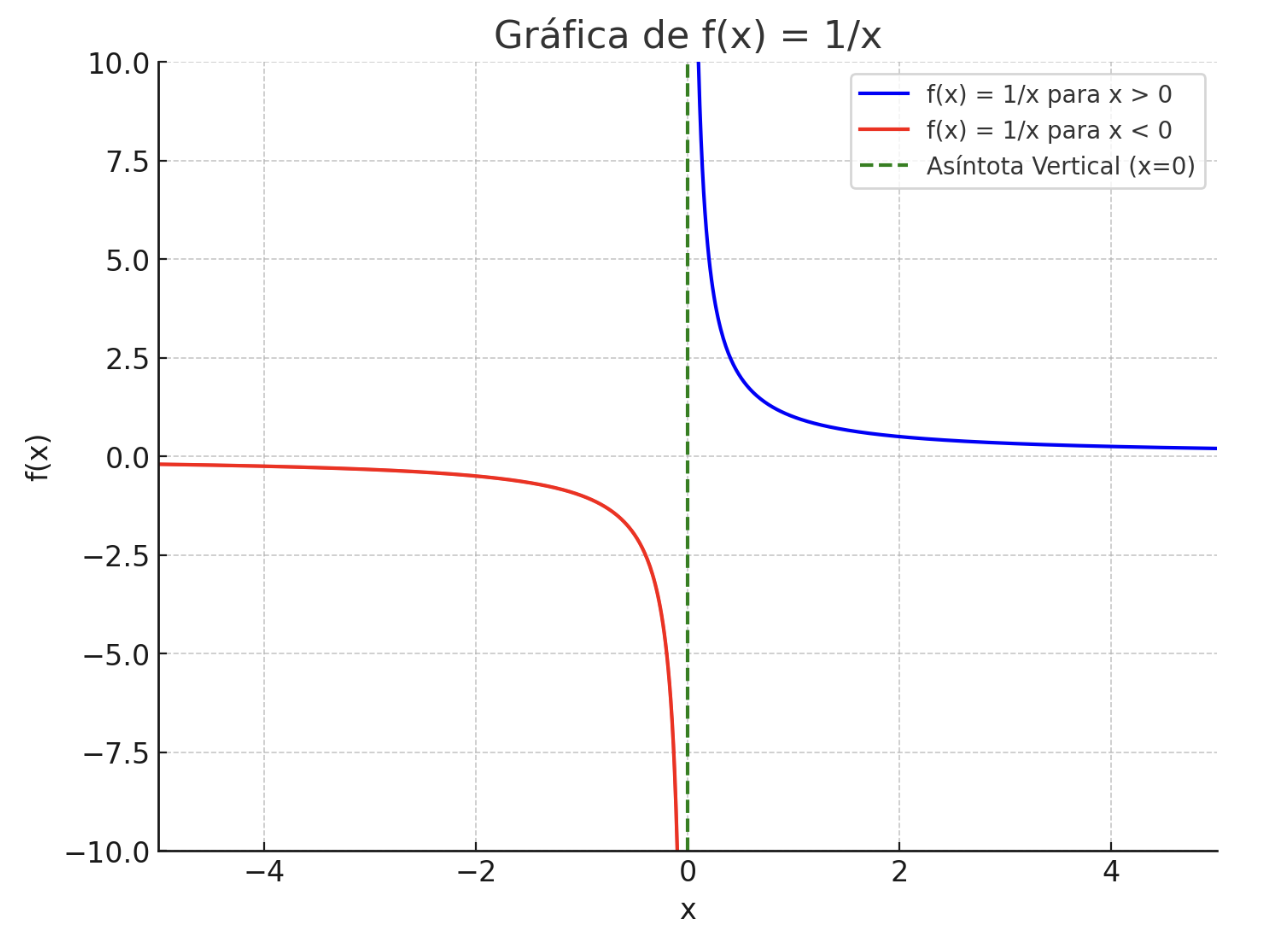
Esta gráfica muestra dos curvas: una para $x>0$ (en azul) y otra para $x<0$ (en rojo). La línea vertical verde indica la asíntota vertical en $x=0$, donde la función no está definida y los valores de $f(x)$ tienden a infinito positivo o negativo a medida que $x$ se acerca a cero desde la derecha o la izquierda, respectivamente. La gráfica ilustra claramente cómo el valor de la función se vuelve muy grande en magnitud a medida que $x$ se acerca a cero.

Similarmente, el logaritmo de un número que se acerca a cero desde el lado positivo se vuelve cada vez más negativo. Aquí tienes la gráfica de la función \( f(x) = \ln(x) \) (logaritmo neperiano de \( x \)).

En este caso, si estudiamos los límites laterales para tratar de obtener el límite de la función cuando x tiende a cero, nos encontramos que el límite lateral por la izquierda no existe porque no podemos poner valores negativos al argumento de un logaritmo, por lo que solo existe el límite lateral por la derecha:

$\underset {x \to 0}{lim} \left( \ln(x) \right)=\text{No Existe}$

En esta gráfica, se muestra la curva de \( f(x) \) para valores de \( x \) mayores que cero. La línea vertical verde indica la asíntota vertical en \( x = 0 \), donde la función tiende a \( -\infty \) a medida que \( x \) se acerca a cero desde la derecha. Esta gráfica ilustra cómo el valor de la función se vuelve negativamente grande a medida que \( x \) se acerca a cero, reflejando el comportamiento característico del logaritmo natural cerca del origen. Como puedes observar, el hecho de que no exista uno de los límites laterales no condiciona la existencia o no de la asíntota vertical, ésta existe desde el momento en que uno de los límites laterales se va a infinito positivo o negativo.

Ejemplo: Evaluación del tiempo de descomposición en un proceso de compostaje.

El tiempo que tarda en descomponerse cierta cantidad de material se puede modelar usando una función logarítmica, específicamente el logaritmo neperiano. La fórmula para calcular el tiempo de descomposición $T$ (en días) en función de la cantidad de material $M$ (en kilogramos) es:   $T = a \cdot \ln(b \cdot M)$, donde $a$ y $b$ son constantes que dependen de las condiciones del proceso de compostaje, como la temperatura, la humedad, y la composición del material.

Este modelo es útil para la empresa de gestión de residuos para planificar y optimizar su proceso de compostaje, asegurando una descomposición eficiente del material en un tiempo adecuado, lo que a su vez contribuye a una mejor gestión del suelo y del ciclo de nutrientes.

Límite de una función en el infinito

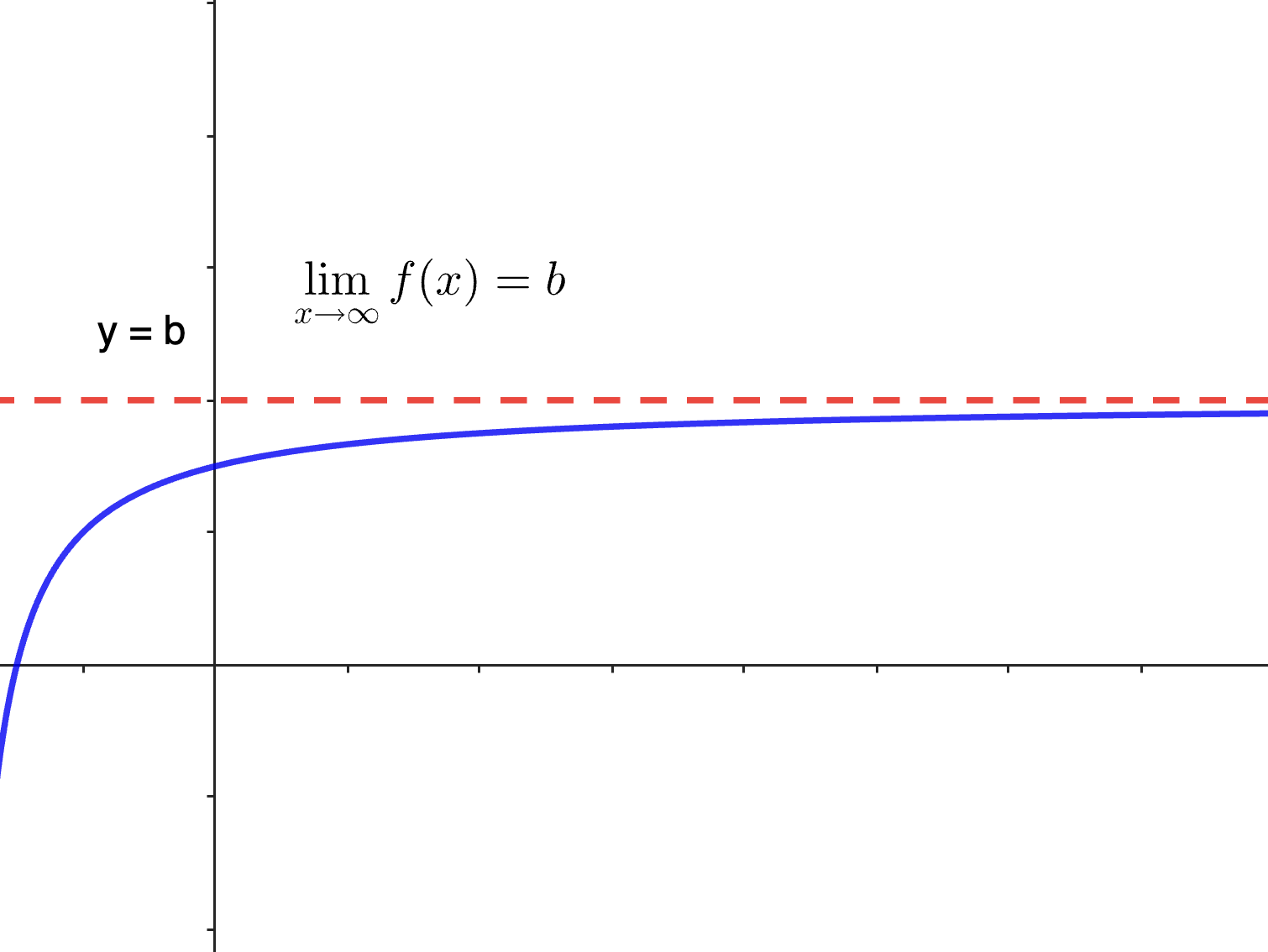
El comportamiento de una función cuando $x$ tiende al infinito (ya sea $+\infty$ o $−\infty$) se refiere a lo que sucede con los valores de esa función a medida que $x$ se hace muy grande en magnitud, ya sea positiva o negativamente. Analizar este comportamiento nos ayuda a entender las tendencias a largo plazo de la función y es útil en varios contextos, como en matemáticas, física, economía, ingeniería, y más.

Estas son algunas utilidades del análisis del comportamiento de una función en el infinito:

• Comportamiento asintótico: Nos ayuda a entender cómo se comporta una función a medida que nos alejamos cada vez más del origen en el eje $x$. Por ejemplo, si una función se acerca a una línea horizontal a medida que $x$ tiende al infinito, esa línea se llama una asíntota horizontal.
• Crecimiento/decrecimiento a largo plazo: En economía y finanzas, por ejemplo, es fundamental comprender si una función relacionada con el crecimiento de una inversión, población o similar, se estabiliza, crece indefinidamente o disminuye a largo plazo.
• Estimación y simplificación de modelos: En ingeniería y física, a menudo simplificamos modelos complejos considerando su comportamiento en el infinito. 

Ejemplo: Incentivo de Ventas en una empresa de tecnología.

Una empresa de tecnología implementa un nuevo plan de incentivos de ventas para su equipo de ventas. El plan está diseñado para aumentar las comisiones a medida que aumentan las ventas, pero con una tasa de crecimiento que disminuye a medida que las ventas alcanzan niveles muy altos, reflejando la dificultad adicional de conseguir ventas en un mercado altamente competitivo.

La función que describe las comisiones totales (en miles de euros) en función de las ventas (en millones de euros) es: $

Una empresa de tecnología implementa un nuevo plan de incentivos de ventas para su equipo de ventas. El plan está diseñado para aumentar las comisiones a medida que aumentan las ventas, pero con una tasa de crecimiento que disminuye a medida que las ventas alcanzan niveles muy altos, reflejando la dificultad adicional de conseguir ventas en un mercado altamente competitivo.

La función que describe las comisiones totales (en miles de dólares) en función de las ventas (en millones de dólares) es:

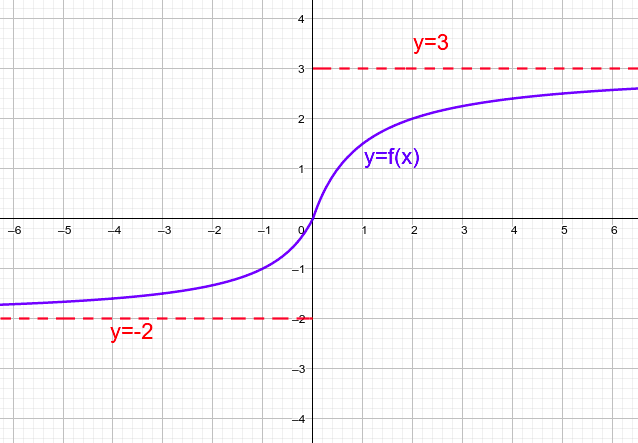
     $f(x) = 5 - {\large{\frac{5}{x + 1}}}$, donde $x$ representa las ventas totales de la empresa.

1. ¿Cuál es el comportamiento de las comisiones a medida que las ventas aumentan?
2. Especialmente, ¿cuál es el límite de las comisiones cuando las ventas tienden al infinito?

Solución: 

Calculamos el límite de $f(x)$ cuando $x$ tiende a infinito:   $\underset {x \to \infty}{lim} \left( 5 - {\large{\frac{5}{x + 1}}} \right)$ 

A medida que $x$ se hace muy grande, el término ${\large{\frac{5}{x + 1}}}$​ se acerca a 0. Por lo tanto, el límite de la función será 5.

La gráfica muestra cómo las comisiones aumentan a medida que aumentan las ventas, pero con una tasa de crecimiento que disminuye a medida que las ventas alcanzan niveles más altos, estabilizándose finalmente en torno a los 5 millones de euros. ​

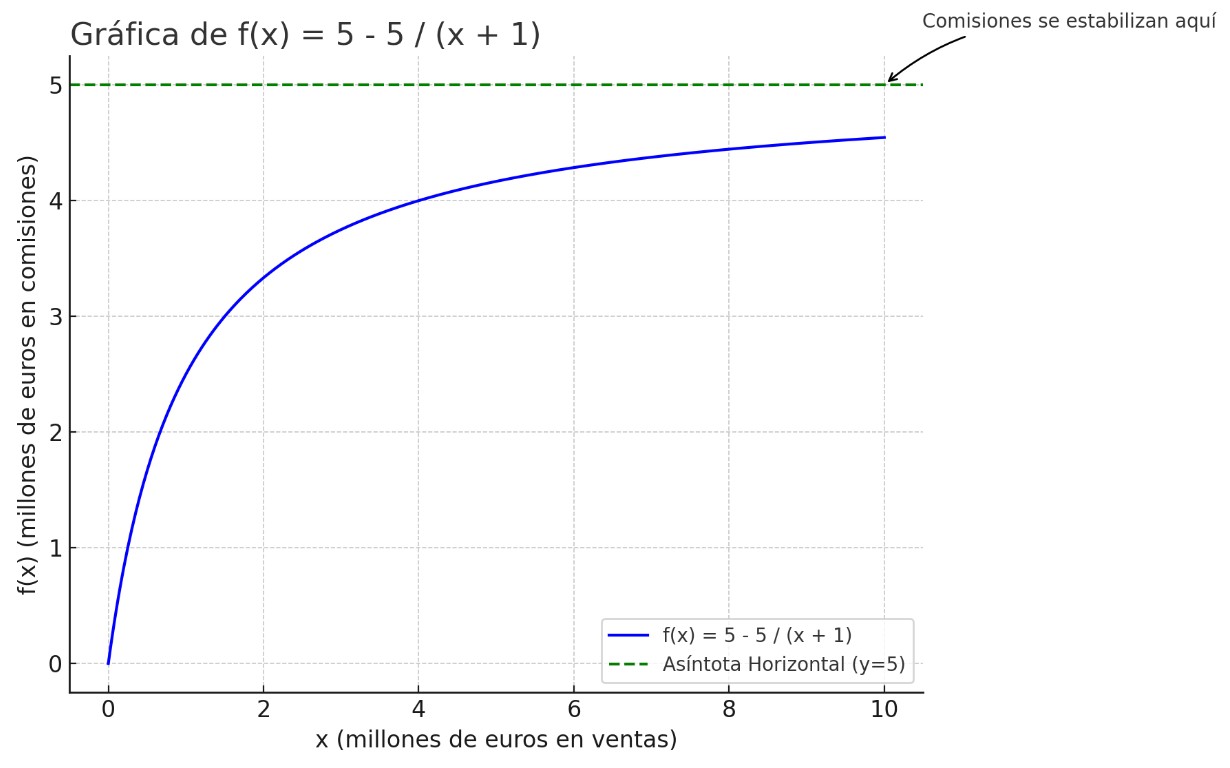
Línea horizontal verde representa la asíntota horizontal en $y=5$. Muestra que las comisiones tienden a estabilizarse en 5 millones de euros.

Para calcular el límite de una función, en la práctica, se siguen ciertos pasos y se consideran varios métodos, dependiendo de la naturaleza de la función y del punto en el que se busca el límite.

1. Evaluación Directa. Comienza evaluando la función directamente en el punto de interés. Si obtienes un número real, que no sea una forma indeterminada como los casos ${\large{\frac{0}{0}}}$, ${\large{\frac{\infty}{\infty}}}$​, $0⋅\infty$, $\infty-\infty$, ese es el límite.

Ejemplo: para $ \underset{x \to 3}{lim} (2x + 1) $, simplemente sustituye \( x \) por 3. Así obtenemos que $ \underset{x \to 3}{lim} (2x + 1)=2·3+1=7 $

2. Factorización y Simplificación. Si la evaluación directa conduce a una forma indeterminada ${\large{\frac{0}{0}}}$, intenta factorizar y simplificar la expresión. Luego, vuelve a evaluar el límite.

Ejemplo: para calcular el límite de la función $ \underset{x \to 2}{lim} {\large{\frac{x^2 - 4}{x - 2}}}$, seguimos los siguientes pasos:

a. $\textbf{Simplificación de la Función}$:
   La función se puede simplificar factorizando el numerador:
   \[ \frac{x^2 - 4}{x - 2} = \frac{(x + 2)(x - 2)}{x - 2} \]
   Simplificando, cancelamos \( x - 2 \) en el numerador y el denominador, obtenemos:    $ x + 2 $

 b. $\textbf{Calculando el Límite}$:
   Ahora, calculamos el límite de la función simplificada:

   $ \underset{x \to 2}{lim}(x+2)$

   Sustituyendo \( x \) por 2, obtenemos:   $ 2 + 2 = 4 $

En el siguiente vídeo se muestran ejemplos de límites que conducen a la forma indeterminada $\frac{0}{0}$.

3. Límites en Infinito. Para calcular límites cuando \( x \) tiende a infinito y la función \( f(x) \) es un cociente de polinomios, es decir, \( f(x) = \frac{P(x)}{Q(x)} \) donde \( P(x) \) y \( Q(x) \) son polinomios, se sigue un procedimiento específico basado en el grado de los polinomios en el numerador y en el denominador. Aquí están los pasos generales:

$\textbf{Identifica el Grado de los Polinomios}$:
    Determina el grado (el mayor exponente) de cada polinomio, tanto en el numerador como en el denominador.

$\textbf{Caso 1: Grado del Numerador es Menor que el del Denominador}$:
    Si el grado de \( P(x) \) es menor que el grado de \( Q(x) \), el límite es 0.

    Ejemplo:  $ \underset{x \to \infty}{lim}{\large{\frac{x^2 + 1}{x^3 + 2x}}}=0$.

$\textbf{Caso 2: Grado del Numerador es Igual al del Denominador}$:
    Si el grado de \( P(x) \) es igual al grado de \( Q(x) \), el límite es el cociente de los coeficientes de los términos de mayor grado de \( P(x) \) y \( Q(x) \).

    Ejemplo:  $ \underset{x \to \infty}{lim}{\large{\frac{3x^2 + 2}{2x^2 + 5}}}={\large{\frac{3}{2}}}$.

$\textbf{Caso 3: Grado del Numerador es Mayor que el del Denominador}$:
    Si el grado de \( P(x) \) es mayor que el grado de \( Q(x) \), el límite es infinito o menos infinito, dependiendo de los signos de los términos de mayor grado.

    Ejemplo: $ \underset{x \to \infty}{lim}{\large{\frac{x^3 + 1}{x^2 + 2}}}=\infty$.

Este método se basa en la idea de que, a medida que \( x \) se hace muy grande, los términos de mayor grado en los polinomios dominan el comportamiento de la función, y los términos de menor grado se vuelven insignificantes en comparación.

Una función es continua en un punto si no hay saltos, rupturas, ni agujeros en ese punto. Esto significa que puedes dibujar el gráfico de la función en ese punto sin levantar el lápiz del papel. Esta idea se extiende a todo un intervalo: una función es continua en un intervalo si es continua en cada punto del intervalo.

Veamos dos vídeos explicativos donde se desarrolla el concepto de función continua:

La definición formal de continuidad en un punto se basa en tres condiciones que deben cumplirse para un valor específico $x=a$:

1. La función debe estar definida en \( a \): \( f(a) \) debe existir.
2. El límite de la función cuando \( x \) se acerca a \( a \) debe existir: $\underset{x \to a}{lim} \text{  }f(x)$ debe existir. Para ello deben existir los dos límites laterales y valer lo mismo.
3. El valor de la función en \( a \) debe ser igual al límite de la función cuando \( x \) se acerca a \( a \): $\underset{x \to a}{lim} \text{  }f(x)=f(a)$.

Existen numerosos ejemplos de funciones que son continuas en su dominio como: las afines, cuadráticas, las polinómicas en general, exponenciales y logarítmicas. Cada una de estas funciones no presenta saltos, rupturas ni agujeros en su gráfico dentro de su dominio. 

Las funciones continuas son muy frecuentes en las modelizaciones de situaciones de la vida cotidiana y en diversas aplicaciones prácticas. La razón de esto se debe a varias características útiles de las funciones continuas:

• Muchos fenómenos naturales y procesos en la vida cotidiana cambian de manera suave y gradual. Las funciones continuas son ideales para modelar tales situaciones, ya que no presentan saltos abruptos o discontinuidades.
• Las funciones continuas son más fáciles de analizar y manipular en cálculo.
• En física, muchas leyes y principios se expresan mediante funciones continuas, como las leyes del movimiento, termodinámica, electromagnetismo, etc. En ingeniería, se usan para modelar comportamientos de materiales, sistemas electrónicos, dinámica de fluidos, y más.
• En economía, las funciones continuas se utilizan para modelar comportamientos de mercados, teorías de consumo y producción, elasticidades, entre otros. En finanzas, son útiles para modelar flujos de efectivo, valoraciones de inversiones, etc.
• Se emplean para modelar fenómenos en psicología, sociología (como distribuciones de poblaciones), y en biología (crecimiento de poblaciones, difusión de sustancias, etc.).

Si una función no es continua en un punto, se dice que es discontinua. Hay varios tipos de discontinuidad, como:

• Discontinuidad evitable: existe un "agujero" en el gráfico de la función, pero podría "rellenarse" para hacer la función continua.
• Discontinuidad de salto: hay un salto abrupto en el gráfico de la función.
• Discontinuidad esencial: el comportamiento de la función cerca del punto es caótico o indefinido, como una asíntota vertical.

La función cuya gráfica se muestra a abajo presenta los 3 tipos de discontinuidad: En $x = 0$ es discontinua evitable, en $x = 1$ y $x = -2$ es discontinua de salto y en $x = -3$ presenta una discontinuidad esencial. Al estudiarlo con los límites laterales se puede ver más claro:

• En el caso de la evitable ($x=0$), los dos límites laterales coinciden, pero la función no existe, por izquierda y derecha la función llega al mismo valor (4).
• En el caso de la de salto, en algunos libros las llaman de salto finito, ($x=1$), los límites laterales existen y toman valores finitos, pero diferentes entre si, por la izquierda se aproxima a 3 y por la derecha a 1.
• En el caso de la esencial, en algunos libros las llaman de salto infinito, ($x=-3$), alguno de los límites laterales se va a $+\infty$ o $-\infty$.

El Teorema de Bolzano es un resultado fundamental en cálculo y análisis matemático. Este teorema establece que si tienes una función continua $f(x)$ en un intervalo cerrado $[a,b]$, y los valores de la función en los extremos del intervalo, $f(a)$ y $f(b)$, tienen signos opuestos (es decir, uno es positivo y el otro negativo), entonces existe al menos un punto $c$ en el intervalo $(a,b)$ donde $f(c)=0$.

Por ejemplo, la función $f(x)=x^2-2$ tiene un cero entre 0 y 2. Es decir, existe un valor $c$, con $0<c<2$ donde $f(c)=0$.

La gráfica muestra la función $f(x)=x^2−2$ en el intervalo $[0,2]$, ilustrando el Teorema de Bolzano:

La función es continua en todo $\mathbb{R}$, en particular también lo es en el intervalo $[0,2]$.

En $a=0$, la función $f(a)$ es negativa (marcada en rojo).
En $b=2$, la función $f(b)$ es positiva (marcada en azul).
Existe un punto $c$ en el intervalo $(0,2)$, específicamente $c=\sqrt{2}$​ (aproximadamente 1.41), donde la función corta al eje x, es decir, $f(c)=0$ (marcado en verde).

Este teorema es especialmente útil para demostrar la existencia de raíces en ecuaciones dentro de un intervalo específico. Sin embargo, es importante notar que el teorema asegura la existencia de la raíz, pero no proporciona un método para encontrarla exactamente. En la práctica, se utilizan métodos numéricos como el método de bisección para encontrar aproximaciones de estas raíces.

El método de bisección es sencillo pero eficaz. A continuación, se explica cómo se debe aplicar.

Método de Bisección

El método de bisección es un algoritmo numérico para encontrar aproximaciones de las raíces de una función continua $f(x)$ en un intervalo $[a, b]$. El método se basa en el Teorema del Bolzano, que asegura que si $f(a)$ y $f(b)$ tienen signos opuestos, entonces existe al menos una raíz en el intervalo.

Algoritmo

1. Comenzar con un intervalo inicial $[a, b]$ donde $f(a) \cdot f(b) < 0$.
2. Calcular el punto medio del intervalo, $c = {\large{\frac{a + b}{2}}}$.
3. Evaluar $f(c)$.
4. Determinar el nuevo intervalo:

• Si $f(c)$ es suficientemente cercano a cero, o si la longitud del intervalo es menor que la tolerancia deseada, entonces detener el algoritmo.
• Si $f(a) \cdot f(c) < 0$, entonces la raíz está en el intervalo $[a, c]$. Hacer $b = c$.
• Si $f(b) \cdot f(c) < 0$, entonces la raíz está en el intervalo $[c, b]$. Hacer $a = c$.

5. Repetir los pasos 2 a 4 hasta alcanzar la precisión deseada.
El método termina cuando se encuentra una aproximación de la raíz con un error menor a la tolerancia especificada.

La ilustración siguiente muestra un diagrama de flujo del algoritmo. Si pinchas sobre la imagen te aparecerá en un recuadro con un botón en forma de aspa para verla en pantalla completa y puedas distinguir claramente el texto de cada elemento.

En la siguiente aplicación puedes comprobar la eficiencia del método de bisección aplicado a la función del ejemplo anterior $f(x)=x^2-2$ para hallar, de forma aproximada, el punto de corte con el semieje positivo $x$,  $c=\sqrt{2}$.

Modifica los valores del intervalo inicial [a,b] (donde se encuentra la raíz o cero de la función) moviendo los deslizadores. Al hacer clic sobre el botón Calcular se aplica el método y se muestran los intervalos obtenidos y el valor de $c$ en cada iteración. Observa el valor de $c$ obtenido y compáralo con el valor de $c=\sqrt{2}=1.4142...$ esperado. Con unas pocas iteraciones conseguimos una aproximación de la raíz con un error inferior a una centésima.

En el siguiente vídeo se explica el Teorema de Bolzano y cómo se aplica el Método de Bisección.