3. Función cuadrática: aplicaciones

1. Función cuadrática: la parábola

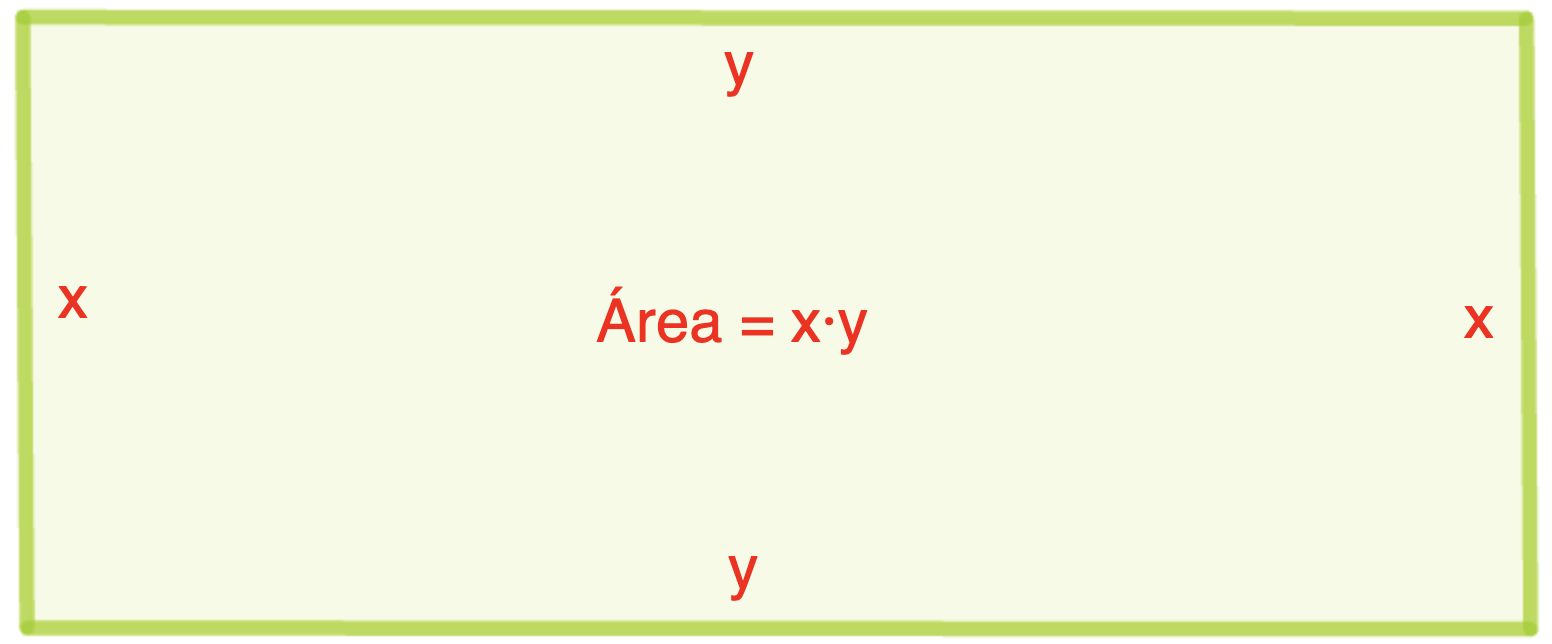
Una función cuadrática es una función matemática de la forma $f(x) = ax^2 + bx + c$, donde $a$, $b$, y $c$ son constantes y $a ≠ 0$. La gráfica de esta función es una parábola. Esto significa que la forma general de la gráfica es una curva en forma de U o una U invertida, dependiendo del valor de $a$ (el coeficiente de $x^2$).

Dirección de la parábola: Si $a > 0$, la parábola se abre hacia arriba. Si $a < 0$, la parábola se abre hacia abajo.
Vértice de la parábola: El vértice de la parábola es el punto más alto o más bajo de la curva, dependiendo de si la parábola se abre hacia arriba o hacia abajo, respectivamente. La coordenada $x$ del vértice se encuentra en $x = - {\large{\frac{b}{2a}}}$, y se puede calcular la coordenada $y$ correspondiente al sustituir este valor en la función cuadrática: $y = f \left(- {\large{\frac{b}{2a}}}\right)$.
Eje de simetría: La parábola tiene un eje de simetría vertical que pasa a través de su vértice. Este eje es la línea vertical $x =\left(- {\large{\frac{b}{2a}}}\right)$.
Punto de intersección con el eje Y: La parábola siempre cruza el eje y en el punto $(0, c)$, ya que cuando $x = 0$, la función cuadrática se reduce a $f(0) = c$.
Puntos de intersección con el eje X (Raíces): Las intersecciones de la parábola con el eje X (si existen) son las soluciones de la ecuación cuadrática $ax^2 + bx + c = 0$. Estas raíces pueden ser reales y distintas, reales e iguales (en el caso de una parábola que toca el eje X en su vértice). Si la ecuación no tiene solución significa que la parábola no corta al eje X.

Ejemplo:

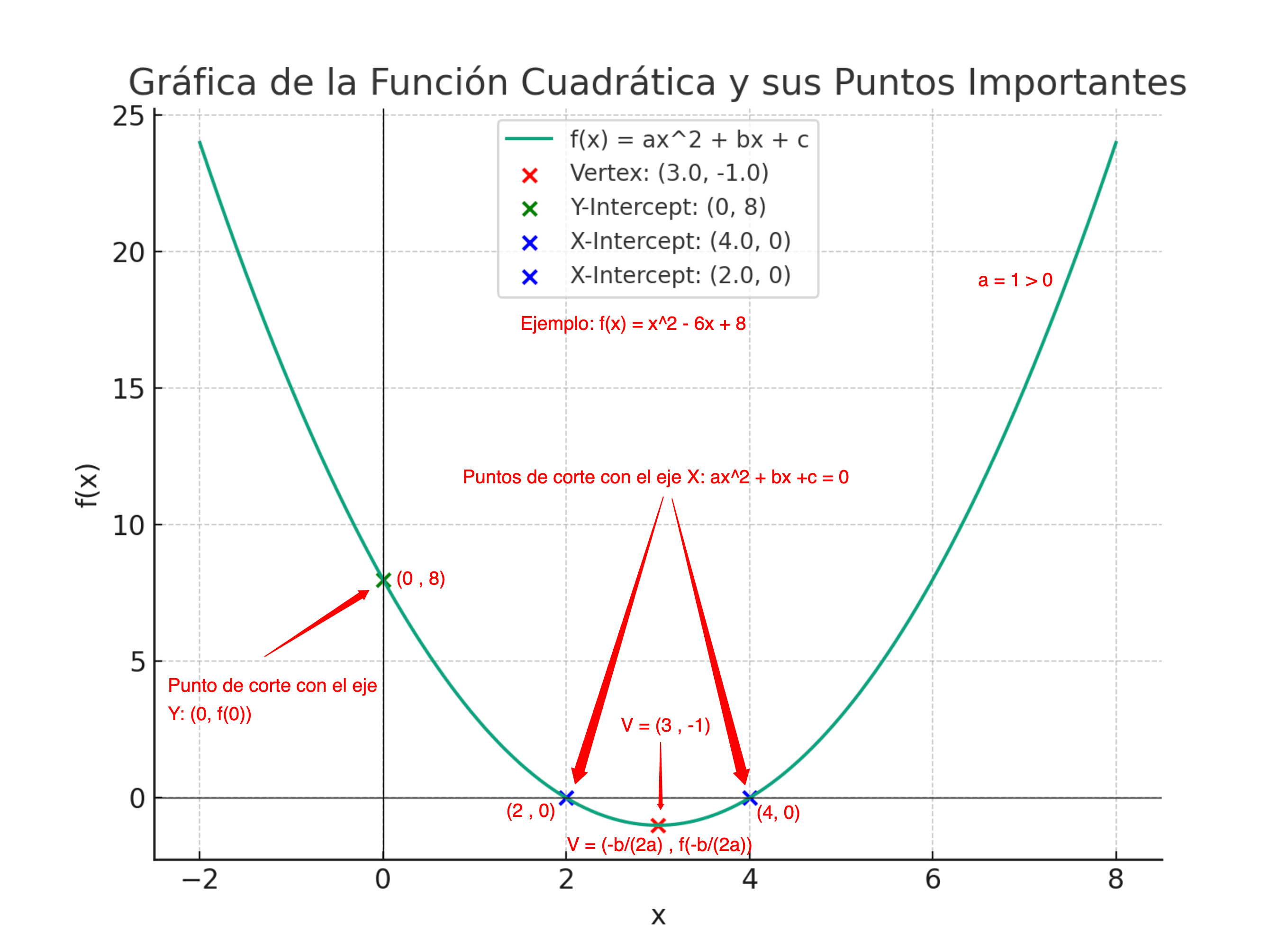
Sea la función cuadrática $f(x) = x^{2} - 6x + 8$. Vamos calcular los puntos de corte con los ejes y el vértice. Con la información obtenida podemos realizar la gráfica de la parábola correspondiente con cierta precisión.

Puntos de intersección con el eje X (Raíces): Son aquellos puntos que deben cumplir que $f(x) = 0$, es decir, $x^2 - 6x + 8 = 0$. Aplicando la fórmula general de la ecuación de 2º grado obtenemos,

$x = {\large{ \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}}}$

$x = {\large{ \frac{-(-6) \pm \sqrt{(-6)^2 - 4 \cdot 1 \cdot 8}}{2 \cdot 1}}}$

$x = {\large{ \frac{6 \pm \sqrt{36 - 32}}{2}}}= {\large{ \frac{6 \pm \sqrt{4}}{2}}}= {3 \pm 1}\rightarrow$ ${\Large{\left\{x_{1}=3+1=4 \atop x_{2}=3-1=2 \right.}}$

Puntos de corte: $(2, 0)$ y $(4, 0)$

Punto de intersección con el eje Y: el punto debe ser $(0, f(0)) = (0, 8)$

Vértice de la parábola: $V = \left(- {\large{\frac{b}{2a}}}, f \left(- {\large{\frac{b}{2a}}}\right)\right) = (3, f(3)) = (3, -1)$

La gráfica es la siguiente:

Infografía de elaboración propia. *Gráfica de la función.* (CC BY-NC-SA)

2. Ejercicios resueltos

Calcula los puntos de intersección con los ejes y el vértice de cada una de las siguientes parábolas y represéntalas gráficamente:

$f(x)= -2x^2+4x+2$
$f(x)= x^2+6x$
$f(x)= 3x^2+12x+6$

Soluciones

El vértice de una parábola dada por $f(x) = ax^2 + bx + c$ se encuentra en $V = \left(- {\large{\frac{b}{2a}}}, f \left(- {\large{\frac{b}{2a}}}\right)\right)$

1. Para $f(x) = -2x^2 + 4x + 2$:

$ {\large{x_{\text{vértice}}}} = -{\large{\frac{b}{2a}}} = -{\large{\frac{4}{2 · (-2)}}} = 1 $; $ {\large{y_{\text{vértice}}}} = f(1) = -2 · 1^2 + 4 · 1 + 2 = 4$; Por lo tanto, el vértice es $(1, 4)$.

La intersección con el eje Y ocurre cuando $x = 0$. Sustituyendo en $f(x)$:

$ y = f(0) = -2 · 0^2 + 4 · 0 + 2 = 2$ . Entonces, la parábola corta el eje Y en $(0, 2)$.

Las intersecciones con el eje X se encuentran resolviendo $f(x) = 0$.

$ -2x^2 + 4x + 2 = 0 $. Aplicando la fórmula cuadrática: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] \[ x = \frac{-4 \pm \sqrt{4^2 - 4 · (-2) · 2}}{2 · (-2)} \] \[ x = \frac{-4 \pm \sqrt{16 + 16}}{-4} \]

$ x = {\large{\frac{-4 \pm \sqrt{32}}{-4}}} \rightarrow$ $ x = {\large{\frac{-4 \pm 4\sqrt{2}}{-4}}} \rightarrow$ $ x = {1 \pm \sqrt{2}}\rightarrow$ ${\Large{\left\{x_{1}=1-\sqrt{2} \approx -0.41 \atop x_{2}=1+\sqrt{2} \approx 2.41 \right.}}$

Resolviendo para las dos soluciones, obtenemos los puntos de intersección con el eje X: $(-0.41, 0)$ y $(2.41, 0)$

Parábola. — Imagen de elaboración propia. *Gráfica de la parábola.* (CC BY-NC-SA)

2. Para $f(x) = x^2 + 6x$:

\[ x_{\text{vértice}} = -\frac{b}{2a} = -\frac{6}{2 · 1} = -3 \] \[ y_{\text{vértice}} = f(-3) = (-3)^2 + 6 · (-3) = 9 - 18 = -9 \] Por lo tanto, el vértice es $(-3, -9)$.

La intersección con el eje Y ocurre cuando $x = 0$. Sustituyendo en $f(x)$:

\[ y = f(0) = 0^2 + 6 · 0 = 0 \] Entonces, la parábola corta el eje Y en $(0, 0)$.

Las intersecciones con el eje X se encuentran resolviendo $f(x) = 0$.

\[x^2 + 6x = 0 \] Factorizando $x$: \[ x(x + 6) = 0 \] Por lo tanto, las soluciones son: \[ x = 0 \quad \text{y} \quad x = -6 \] Entonces, los puntos de intersección con el eje X son $(0, 0)$ y $(-6, 0)$.

3. Para $f(x) = 3x^2 + 12x + 6$:

\[ x_{\text{vértice}} = -\frac{b}{2a} = -\frac{12}{2 · 3} = -2 \] \[ y_{\text{vértice}} = f(-2) = 3 \cdot (-2)^2 + 12 · (-2) + 6 = 12 - 24 + 6 = -6 \] Por lo tanto, el vértice es $(-2, -6)$.

La intersección con el eje Y ocurre cuando $x = 0$. Sustituyendo en $f(x)$:

\[ y = f(0) = 3 · 0^2 + 12 · 0 + 6 = 6 \] Entonces, la parábola corta el eje Y en $(0, 6)$.

Las intersecciones con el eje X se encuentran resolviendo $f(x) = 0$.

Aplicando la fórmula cuadrática: \[x = \frac{-12 \pm \sqrt{12^2 - 4 · 3 · 6}}{2 · 3} \] \[ x = \frac{-12 \pm \sqrt{144 - 72}}{6} \]

$ x = {\large{\frac{-12 \pm \sqrt{72}}{6}}} \rightarrow$ $ x = {\large{\frac{-12 \pm 6 \sqrt{2}}{6}}} \rightarrow$ $ x = -2 \pm \sqrt{2} \rightarrow$ ${\Large{\left\{x_{1}=-2+\sqrt{2} \approx -0.59 \atop x_{2}=-2-\sqrt{2} \approx -3.41 \right.}}$

Entonces, los puntos de intersección con el eje X son $(-0.59, 0)$ y $(-3.41, 0)$

3. Aplicaciones de la parábola

Las parábolas se encuentran en muchas aplicaciones de la vida cotidiana, desde la tecnología hasta el deporte.

Puente de las Cataratas Victoria, Zimbabue — Harvey Barrison. *Puente de las Cataratas Victoria.* (CC BY-NC-SA)

Algunas de las aplicaciones más comunes de las parábolas son:

Trayectorias de proyectiles: Cuando lanzamos una pelota o cualquier otro objeto en el aire, su trayectoria forma una parábola. Esto es debido a la combinación de la gravedad actuando hacia abajo y la velocidad inicial del objeto en una dirección.
Reflectores y antenas parabólicas: Los reflectores de faros de automóviles y las antenas parabólicas tienen formas parabólicas. Esta forma es ideal para reflejar la luz o las señales hacia un punto focal específico, lo que mejora la eficiencia de estas tecnologías.
Puentes y arquitectura: Algunos diseños de puentes utilizan arcos parabólicos debido a sus propiedades estructurales fuertes y estéticamente agradables. En arquitectura, las estructuras con elementos parabólicos pueden ofrecer tanto belleza como funcionalidad. El puente de las Cataratas Victoria (Zimbabue) construido en 1904-1905, tiene un arco parabólico con una luz¹ de 151 metros, lo que lo convierte en uno de los puentes con arco parabólico más largos del mundo.
Fuentes de agua: El chorro de agua de una fuente generalmente forma una parábola, especialmente cuando se dispara verticalmente hacia arriba y cae bajo la influencia de la gravedad.
Cálculo de trayectorias en deportes: En deportes como el baloncesto, golf o fútbol, calcular la trayectoria parabólica de la pelota puede ser crucial para lograr un tiro exitoso o un pase preciso.

En el siguiente vídeo se explica por qué las antenas parabólicas tienen una forma parabólica.

Video de Derivando. ¿Por qué las Antenas Parabólicas son parabólicas?
(Licencia estándar de YouTube)

4. Tu primer reto

Dispones de 100 metros de valla para cercar un terreno rectangular. El objetivo es determinar las dimensiones del rectángulo que maximizarán el área encerrada por la valla.

Es decir, debes construir un rectángulo utilizando exactamente 100 metros de valla. No hay limitaciones en cuanto a la longitud o anchura del rectángulo, pero la suma total del perímetro² debe ser 100 metros.

El reto que se plantea es responder a la pregunta: ¿Cuáles deben ser las dimensiones del rectángulo (longitud y anchura) para encerrar la mayor área posible?

Pista 1

Observa que un mismo perímetro puede encerrar diferentes áreas.

Imagen de elaboración propia. *Rectángulos* (CC BY-NC-SA)

Pista 2

Podemos expresar el área de un rectángulo en función de uno de sus lados, denominado $x$. Considerando que el perímetro del rectángulo es de 100 metros, es decir, $2x +2y =100$, podemos simplificar esta ecuación dividiéndola por 2, obteniendo así $x +y = 50$.

A partir de esta simplificación, deducimos que $y = 50 - x$. En consecuencia, la fórmula para calcular el área del rectángulo, denotada como $A$, se expresa mediante la ecuación $A = x·y = x·(50-x)$.

Por lo tanto, la expresión del área en función de $x$ se convierte en $A(x)=x·(50-x)=50x-x^2$. Esta es una función cuadrática cuya representación gráfica es una parábola.

Imagen de elaboración propia. *Fórmula del área.* (CC BY-NC-SA)

Pista 3

Representa gráficamente la función y observa cómo varía el área a medida que aumentamos la longitud del lado $x$.

En la siguiente imagen interactiva, se ilustra la parábola correspondiente a la función $A(x) = 50x - x^2$. Para cada valor de $x$, se muestra el valor del área $A(x)$ correspondiente. Podemos modificar el valor de $x$ arrastrando el deslizador que se encuentra en la parte inferior. Además, el punto $(x, A(x))$ se resalta de manera destacada.

Imagen interactiva de elaboración propia. Parábola interactiva. (CC BY-NC-SA)

Pista 4

La mayor área posible corresponde a la coordenada $y$ del vértice, que es el punto más elevado de la parábola. La coordenada $x$ asociada indica el valor que debe tener el lado del rectángulo para alcanzar esa área máxima.

Al aplicar la fórmula del vértice de una parábola $V = \left(- {\large{\frac{b}{2a}}}, A \left(- {\large{\frac{b}{2a}}}\right)\right)$, a la parábola $A(x)=50x-x^2$, obtenemos $V= (25,625)$

Esto implica que el valor máximo del área $A(x)$ es 625, alcanzado cuando $x$ es 25.

Observa que cuando $x=25$, entonces $y=25$ (ya que $y=50-x$), lo que indica que estamos ante un cuadrado de lado 25.

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0