2.2. Otros métodos para calcular integrales
 |
| Tejedor Imagen del banco de imágenes del ITE |
En algunas ocasiones las integrales no son tan inmediatas como las que hemos visto hasta ahora, sino que el cálculo de algunas de ellas puede llegar a ser bastante complicado. Ahora vamos a utilizar una técnica para calcular integrales basado en la regla de la cadena. Es decir, si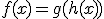 
sabemos que 
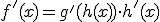. Dándole la vuelta:
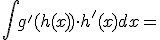
haciendo un cambio de variable y derivando en cada miembro respecto a la variable correspondiente tendríamos:
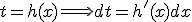
Por tanto
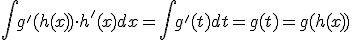
Un desarrollo de este método, llamado de sustitución o de cambio de variable lo tienes en el siguiente PDF:
Ejemplo o ejercicio resuelto
Sabemos que la derivada de un función f(x) es
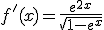
Calcula la función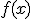 
AV - Reflexión
Calcula la siguiente integral por el método de sustitución: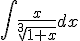 
.
PISTA: intenta el cambio de variable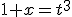 
y consigue una integral en función de t.
Ejemplo o ejercicio resuelto
En esta ocasión te pedimos que calcules la siguiente integral aplicando el método de sustitución.
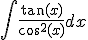
NOTA: Recuerda que si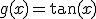 
, entonces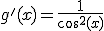 
AV - Reflexión
Calcular por el método de cambio de variable la siguiente integral:
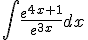
Ejemplo o ejercicio resuelto
 |
| Ciclista. Imagen del banco de imágenes del ITE |
En una empresa de diseño están investigando sobre el rozamiento que ofrece un nuevo casco de ciclista al viento para que lo puedan utilizar los ciclistas de un equipo en la próxima vuelta ciclista a España. Para ese estudio han obtenido la función que proporciona la pendiente de la recta tangente a la forma del casco en cada punto. Esta función es
A partir de esta función, la empresa desea obtener la función cuya gráfica es la forma del casco. ¿Puedes ayudarles?
AV - Reflexión
Calcula la siguiente integral por el método de cambio de variable: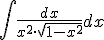 
.
PISTA: Realiza el cambio de variable 
.
Para saber más
Otro método de integración es el de la integral por partes. En el siguiente PDF puedes observar este método resumido y aplicado:
En el siguiente vídeo puedes ver cómo podemos aplicar esta fórmula: