Retroalimentación
Recordemos primeramente todos los pasos que hemos dado hasta llegar aquí, dibujando en los ejes de coordenadas la información que vayamos obteniendo a medida que avanzamos:
a) Dominio: dado que es una función racional su dominio son todos que no anulen el
denominador.
Calculamos los valores que anulan el denominador:
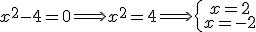
Así el dominio de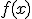 
es 
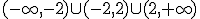
Lo representamos:
b) Simetría: Calculamos
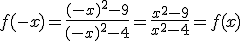
Por tanto, la función es simétrica respecto al eje de ordenadas. La imagen a la izquierda y a la
derecha del eje es la misma.
c) Puntos de corte con los ejes:
c.1) Puntos de corte con el eje OX: Para calcular estos puntos resolvemos el siguiente sistema:
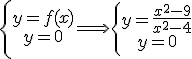
Así, tenemos que:
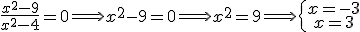
Por tanto los puntos de corte son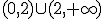 
c.2) Punto de corte con el eje OY: Para calcular este punto de corte resolvemos el siguiente
sistema:
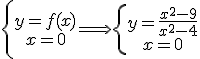
Por tanto tenemos que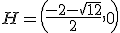 
Por tanto, el punto de corte es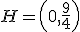 
Lo representamos:
d) Asíntotas de la función: Sabemos que existen tres tipos de asíntotas:
d.1) Asíntotas verticales: Para conocer las asíntotas verticales de la función debemos hacer un
estudio de la continuidad de la misma. En un principio sabemos que este función es continua en su
dominio, es decir, en 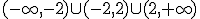. Tenemos que ver el
tipo de discontinuidad que se produce 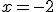en 
y en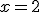 
.
En 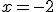estudiamos los límites
laterales:
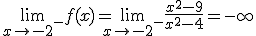
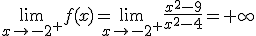
Por tanto en este punto se produce una discontinuidad de salto infinito, luego hay una asíntota
vertical cuya ecución es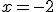
En 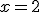estudiamos los límites
laterales:
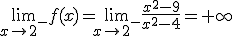
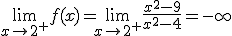
Por tanto en este punto se produce una discontinuidad de salto infinito, luego hay una asíntota
vertical cuya ecución es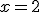
d.2) Asíntotas horizontales: Calculamos los siguientes límites:
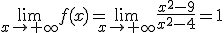
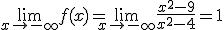
Luego existe una asíntota horizontal cuya ecuación es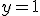 
.
d.3) Asíntotas oblicuas: En este caso, dado que existe una asíntota horizontal, no existe
asíntota oblicua.
Lo representamos:
e) Extremos de la función: Para calcular los extremos de la función debemos seguir una serie
de pasos:
.- En primer lugar debemos calcular la función derivada:
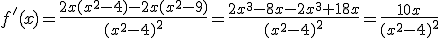
.- Igualamos la derivada a cero para obtener los puntos críticos:
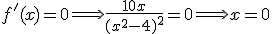Así, esta función tiene un único punto crítico.
.- Calculamos la derivada segunda:
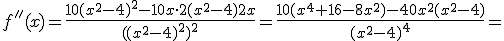
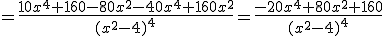
.- Sustituimos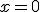 
obteniendo que:
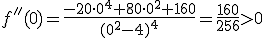
Por tanto tenemos un punto mínimo e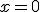n . Las coordenadas de ese
punto son:
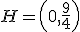
Lo representamos:
f) Monotonía de la función: Para estudiar los intervalos de crecimiento y de decrecimiento
de la función, vamos a ver el signo que tiene la derivada en cada uno de los posibles intervalos.
Para ello recordamos que el dominio de la función es:
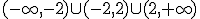
Por otra parte, sabemos que tiene un mínimo en .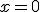
Por tanto el estudio de crecimiento y decrecimiento lo hacemos con la siguiente tabla:
| Intervalo |
 |
 |
 |
|
 |
- |
- |
+ |
+ |
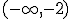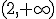
Monotonía
|
Decreciente |
Decreciente |
Creciente |
Creciente |
Luego
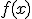es decreciente en 
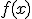es creciente en 
Lo representamos:
Con toda la información anterior, la representación gráfica queda de la siguiente forma:
Una animación de todo el proceso sería:
