Resumen

Una ecuación es una igualdad algebraica que es cierta para algunos valores de las incógnitas y falsa para otros.

Por tanto, la diferencia entre identidad y ecuación es que la identidad siempre es cierta, mientras que la ecuación no.

El valor o valores de la incógnita que hace que la igualdad se cumpla se llama solución de la ecuación.

Las ecuaciones de primer grado son aquellas que tienen la forma ax + b = c.

Una ecuación de segundo grado es una ecuación que tras simplificarla y pasar todos los términos a un lado queda de la forma:

ax² + bx + c = 0.

Para resolverlas se usa la fórmula:

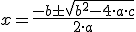
En el caso de ecuaciones incompletas:

• Si falta el término en x, despejar x en la ecuación. Ej: x²-4 = 0 pasa a x=
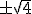
• Si falta el término sin x, sacar factor común x en el miembro de la izquierda y deducimos que si el producto es cero, alguno de los factores ha de ser cero. Ej: x²+x =0, pasa a x·(x+1)=0 que se anula en x=0 o en x=-1

Un tipo de ecuaciones con grado mayor que 2 son las llamadas ecuaciones bicuadradas. Estas ecuaciones son de la forma:

ax⁴ +bx² + c = 0.

Se resuelven reduciéndolas a ecuaciones de segundo grado haciendo el cambio t = x².

Las ecuaciones polinómicas son de la forma P(x) = 0 donde P(x) representa un polinomio de cualquier grado. Teniendo en cuenta esto, las soluciones de la ecuación coinciden con las raíces del polinomio. Por tanto, para resolver la ecuación se factoriza el polinomio y se calculan sus raíces.

Otro tipo de ecuación que se resuelve reduciéndola previamente a una de primer o segundo grado es la ecuación irracional. Una ecuación en la que aparece alguna raíz cuadrada.

El truco está en aislar la raíz; dejarla sola a un lado del símbolo igual, y a continuación, elevar los dos miembros al cuadrado para que desaparezca la raíz.

Las ecuaciones exponenciales son aquellas en las que la incógnita aparece en el exponente, para resolverlas se aplican las propiedades de las potencias o un cambio de variable hasta llegar a una ecuación de la forma a^x=b. Esta se resolverá bien directamente (si b se puede poner como una potencia de base a, igualando los exponentes), bien tomando logaritmos.

Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece en el argumento o en la base del logaritmo. Para resolverlas habrá que aplicar la definición y las propiedades de los logaritmos, y pasarla a una expresión algebraica.

Cuando resolvemos esta ecuación hay que comprobar si las soluciones obtenidas sirven en la ecuación logarítmica ya que la base de un logaritmo puede ser cualquier número positivo menos el 1 y el argumento tiene que ser un número positivo.