4.2. Ecuaciones de grado superior a dos

Veamos un tipo de ecuaciones de grado cuatro muy particulares. Son de la forma:

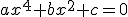
ax^4+bx^2+c=0

El método de resolución de este tipo de ecuaciones se fundamenta en el de la ecuación de segundo grado.

Veamos un ejemplo. Resolvamos la ecuación:

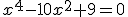
x^4-10x^2+9=0

En primer lugar aplicamos lo que se llama "cambio de variable", utilizando el cambio t=x² quedaría la expresión:

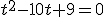
t^2-10t+9=0

ya que x⁴=(x²)²=t², esta ecuación ya es de segundo grado y la resolvemos como tal:

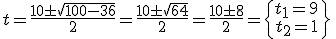
$t=\frac{10\pm\sqrt{100-36}}{2}=\frac{10\pm\sqrt{64}}{2}=\frac{10\pm 8}{2}=\begin{Bmatrix} t_1=9 & \mbox{}&\ _2=1 & \mbox{}&\end{matrix}$

A continuación deshacemos el cambio quedando:

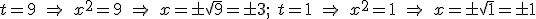
$t=9 \ \Rightarrow \ x^2=9 \ \Rightarrow \ x=\pm\sqrt{9}=\pm3; \ t=1 \ \Rightarrow \ x^2=1 \ \Rightarrow \ x=\pm\sqrt{1} = \pm1$

Por tanto las soluciones son 4: x = -3, -1, 1 y 3.

Importante

Otro tipo de ecuaciones con grado mayor que 2 son las llamadas ecuaciones bicuadradas. Estas ecuaciones son de la forma:

ax⁴ +bx² + c = 0.

Se resuelven reduciéndolas a ecuaciones de segundo grado haciendo el cambio t = x².

En el siguiente vídeo puedes ver algunos ejemplos.

Vídeo de Tuto mate alojado en Youtube

Reflexiona

Intentalo tú ahora:

Comprueba lo aprendido

Veamos ahora ecuaciones de grado superior a dos, pero que no son bicuadradas.

Importante

Las ecuaciones polinómicas son de la forma P(x)=0 donde P(x) representa un polinomio de cualquier grado. Teniendo en cuenta esto, las soluciones de la ecuación coinciden con las raíces del polinomio. Por tanto, para resolver la ecuación se factoriza el polinomio y se calculan sus raíces.

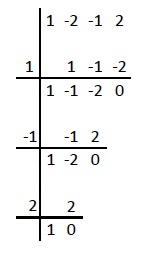Veamos, por ejemplo, la siguiente ecuación:

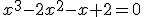
x^3-2x^2-x+2=0

Las posibles raíces enteras del polinomio coincidían con los divisores del término independiente, por tanto aplicamos la regla de ruffini probando con los divisores del 2: 1, -1, 2 y -2

De esta forma las raíces que salen son 1, -1 y 2 que son las soluciones de la ecuación de partida.

En ecuaciones como la anterior no es necesario aplicar Ruffini hasta encontrar las tres raíces.

Cuando aplicamos Ruffini y llegamos a un polinomio de 2.º grado como cociente, lo transformamos en ecuación de segundo grado que podemos resolver y obtener las dos soluciones restantes.

En el ejemplo anterior:

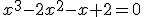
x^3-2x^2-x+2=0

Aplicamos Ruffini y encontramos la primera solución que sería 1:

El cociente resultante de dicha división sería la ecuación de 2.º grado x²-x-2=0, de manera que si resolvemos esta ecuación obtenemos de forma sencilla las otras dos soluciones:

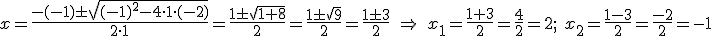
$x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot{1\cdot{(-2)}}}}{2\cdot{1}}=\frac{1\pm\sqrt{1+8}}{2}=\frac{1\pm\sqrt{9}}{2}=\frac{1\pm3}{2}\Rightarrow{x_1=\frac{1+3}{2}=\frac{4}{2}=2};x_2=\frac{1-3}{2}=\frac{-2}{2}=-1$

En el siguiente vídeo puedes ver más ejemplos.

Vídeo de Tuto mate alojado en Youtube

Importante

Otro tipo de ecuación que se resuelve reduciéndola previamente a una del tipo anterior es la ecuación irracional. Una ecuación en la que aparece alguna raíz cuadrada.

El truco está en aislar la raíz; dejarla sola a un lado del símbolo igual, y a continuación, elevar los dos miembros al cuadrado para que desaparezca la raíz.

En el siguiente vídeo tienes más ejemplos resueltos.

Vídeo de Tuto mate alojado en Youtube

Comprueba lo aprendido

Si quieres practicar más, puedes hacer algunos ejercicios que puedes encontrar en este enlace.

4.2. Ecuaciones de grado superior a dos

Importante

Reflexiona

Retroalimentación

Comprueba lo aprendido