4.1. Ecuaciones de segundo grado
 |
| Fotografía de Deborah Bates en Pixabay. Licencia CC. |
Juan es bastante conocedor de las matemáticas y sabe que la figura rectangular que tiene mínimo perímetro con un área fijada es el cuadrado. Es decir, que si queremos que una figura rectangular tenga una determinada superficie y queremos que el material para su construcción sea mínimo, debemos construirlo de forma cuadrada.
Pues bien; Juan desea poner un mostrador expositor con una serie de artículos de complemento que ocupe el centro de su nueva tienda del centro comercial, y según las estimaciones que ha hecho, debe tener una superficie de 6 metros cuadrados, entonces, ¿qué longitud debe tener el expositor?
Si llamamos x a la longitud del lado del cuadrado y puesto que el área de un cuadrado es lado por lado, tendremos que tiene que cumplirse que:
x·x = 6, o lo que es lo mismo, x2 = 6.
Este es un ejemplo de ecuación de segundo grado; una ecuación donde x aparece elevada al cuadrado.
Importante
Una ecuación de segundo grado es una ecuación que tras simplificarla y pasar todos los términos a un lado queda de la forma:
ax2 + bx + c = 0.
Para resolverlas se usa la fórmula:
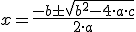
En el siguiente vídeo nos explican con varios ejemplos, cómo se resuelven ecuaciones de segundo grado completas.
Recuerda que siempre "a" es el número que multiplica a x2, "b" el que multiplica a x y "c" el número sin x, teniendo en cuenta en todos los casos los signos.
Vídeo de Tuto mate alojado en Youtube
Reflexiona

Fotografía de StarupStockPhotos en Pixabay. Licencia CC.
En este enlace vas a resolver ecuaciones de segundo grado. Lee las instrucciones y completa los huecos.
Importante
Como puedes ver, a veces hay dos soluciones, a veces una y otras no tienen solución.
Esto depende del número que nos quede dentro de la raíz, o sea, del valor de la expresión
b2 - 4·a·c
que se llama discriminante:
- Si es positivo, hay dos soluciones.
- Si es cero, hay una única solución.
- Si es negativo, no existe solución, pues como sabes, la raíz cuadrada de un número negativo no existe.
Revisa el video de arriba, y comprueba que en cada uno de los ejemplos, se cumple lo explicado en el importante.
Pero...¿y si falta alguien? ¿Qué hacemos? ¿Cómo lo resolvemos?
En numerosas ocasiones, las ecuaciones de segundo grado no quedan completas, sino que falta algún término. Sin ir más lejos, el ejemplo con el que empezamos el apartado anterior, ¿recuerdas el del expositor que quería comprar Juan que ocupara 6 metros cuadrados?, nos daba como ecuación:
x2 = 6 ,
y si lo expresamos como las ecuaciones generales, nos quedaría:
x2 - 6 = 0,
o sea, una ecuación en la que falta el término con x; falta b
Estos casos podemos resolverlos utilizando la fórmula, símplemente dándole al término que falte el valor 0.
Por ejemplo, en la ecuación que acabamos de poner,
x2 - 6 = 0,
si usáramos la fórmula tendríamos que a = 1, b=0, pues no hay término con x y c= -6. Sustituyendo nos quedaría:
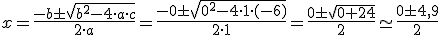
Luego tendríamos que una solución es 4,9/2 =2,45 y la otra - 4,9/2 = -2,45; aunque en el contexto de nuestro problema, como x era la longitud del lado del expositor, la única solución válida sería 2,45 metros.
Pero seguro que estás pensando, ¿y para qué hace todo esto? ¡Si se puede hacer mucho más fácil! ¡Si sólo hay que hacer la raíz cuadrada de 6!, ¿verdad?
Importante
Es mucho más fácil y cómodo utilizar otros métodos.
- Si falta el término en x, despejar x en la ecuación. Ej: x2-4 = 0 pasa a x =
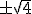
- Si falta el término sin x, sacar factor común x en el miembro de la izquierda y deducimos que si el producto es cero, alguno de los factores ha de ser cero. Ej: x2+x =0, pasa a x·(x+1)=0 que se anula en x=0 o en x=-1
Reflexiona
En los siguientes enlaces puedes practicar ecuaciones incompletas de los dos tipos:
Para saber más
En la animación puedes ver de dónde sale esa fórmula:
Escena en Proyecto Descartes. Licencia CC