1.1. Definición de continuidad de una función

Ya conoces algunas funciones y unas pocas características de las mismas. Ahora nos planteamos estudiar algebraicamente una característica que se observa a simple vista en la gráfica de una función: su continuidad. Gráficamente observamos que una función es continua ya que su gráfica nos se rompe, está hecha de un sólo trazo. Pero no siempre disponemos de la gráfica de una función. Además, esta característica de continuidad va a influir sobre otras como veremos más adelante.

Importante

Si tenemos una función 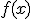diremos que es continua en un punto 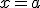cuando se cumpla que:

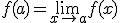
Así, se deben cumplir tres cosas:

1) Que podamos calcular .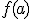

2) Que exista 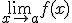para ello sabemos que deben existir los límites laterales y coincidir, es decir:

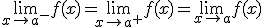
3) Por último, que la función en el punto coincida con el límite, es decir:

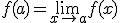
AV - Pregunta Verdadero-Falso

Marca la respuesta correcta en cada caso:

Retroalimentación

Verdadero

Retroalimentación

Verdadero

Retroalimentación

Falso

Retroalimentación

Falso

Importante

De forma análoga a como definimos los límites laterales en el tema 2, podemos hablar de las continuidades laterales de una función.

La función f(x) es continua por la izquierda en 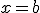si existen 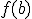y y 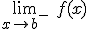se cumple que .

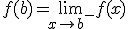Por su parte será continua por la derecha en 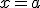si existe 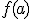y y 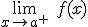se cumple que .

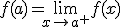Como consecuencia de lo anterior diremos que una función 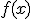es continua en un intervalo 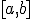si la función es continua en todos los puntos interiores del intervalo y además es continua a la derecha de a y a la izquierda de b. Si el intervalo fuese abierto estas dos últimas condiciones sobrarían.

Ejemplo o ejercicio resuelto

Fábrica de Esther Balgoma Hernando
Imagen obtenida del Banco de imágenes del ITE.

Una fábrica envasadora tiene una cinta por la que circulan las botellas que van a llenarse. Las botellas se llenan a lo largo de una curva descrita por la función 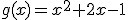. Tras llenarse, en el punto 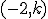se le pone el tapón a las botellas, siguiendo por la curva anterior hasta el punto de abcisa 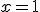en el que las botellas deben seguir una línea recta para llegar al almacén. Todo este proceso se ha automatizado siguiendo la siguiente función:

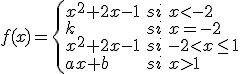
Ahora la máquina se ha desconfigurado y, puesto que la cinta que recorren las botellas no se rompe, debemos investigar sobre qué se debe cumplir para que la función sea continua 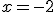en y en 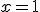.